Motivace posudkového lékaře z pohledu teorie her

Souhrn

Pomocí teorie her se autor zamýšlí nad motivací posudkového lékaře při výkonu jeho činnosti s tím, do jaké míry je motivován posuzovanému nevyhovět v jeho požadavcích.

Klíčová slova:
teorie her – vězňovo dilema – rozhodovací strom

Úvod

Když jsem před časem nastoupil jako kmenový lékař na lékařskou posudkovou službu – tehdy jako součást úřadu práce – o práci posudkového lékaře jsem měl jen rámcové představy. Ocitl jsem se najednou v protikladné dvojroli. Na jedné straně lékař – svojí podstatou sociálně cítící člověk s posláním léčit lidské bolístky a pomáhat. Na druhé straně namísto advokáta zdravotního stavu jeho soudce, pro něhož se z pacienta stal posuzovaný, z klienta protihráč. Od té doby při každé jednotlivé kauze osciluji mezi těmito dvěma póly. Vždy mám na mysli obě polohy tohoto povolání, připadám si jako dvojjediný. Možná i proto, že není jednoduché pro nikoho pregnantně stanovit jednoznačné zadání práce posudkového lékaře. Stanovit míru tvrdosti k žadateli jako posuzovanému, míru empatie k témuž žadateli jako pacientovi. Navíc jsou ve hře paragrafy, které jsou už ze své podstaty ne vždy jednoznačné.

Jaká je vlastně motivace posudkového lékaře hrát jednu či druhou roli? Začnu otázkou – proč by měla být motivace jiná než u každého jiného? Pokusím se pomoci si v zamyšlení nad onou motivací matematickou teorií, abychom se nepohybovali jen v roli esejistického filozofování.

Jedná se o teorii her.

Termín hráči a hřiště, jakkoliv byl přenesen do matematiky a její teorie her ze světa sportu a posléze aplikován v politické ekonomii a sociobiologii, není termínem módním a samoúčelným. Disciplína jako taková vznikla v roce 1944 vydáním publikace Johna von Neumanna a Oskara Morgensterna: „Theory of Games and Economic Behavior“. V teorii her jsou hry formálně definovanými pojmy. Hra obsahuje hráče, jejich možné tahy,akce nebo strategie a funkci udávající zisk každého hráče v závislosti na provedených tazích. Teorie her je disciplína aplikované matematiky, která analyzuje široké spektrum konfliktních rozhodovacích situací, které mohou nastat kdekoliv, kde dochází ke střetu zájmů. Herně-teoretické modely se pak snaží tyto konfliktní situace nejen analyzovat, ale sestavením matematického modelu daného konfliktu a pomocí výpočtů se snaží nalézt co nejlepší strategie pro konkrétní účastníky takových konfliktů [4].

Každá hra má tři základní prvky:

1. hráče;
2. množinu možných akcí (strategií), ze kterých každý jednotlivý hráč volí;
3. výsledek, kterého hráč při každé kombinaci strategií dosáhne.

Jednou z cest, jak shrnout příslušné údaje o hře, je vytvořit jednoduchou tabulku obsahující hráče, strategie a výsledky, která se nazývá výplatní matice hry. Strategie jednoho z hráčů, která mu přinese (zdánlivě) vyšší výnos, ať udělá druhý hráč cokoli, je strategií dominantní. V závorce uvádím u slova vyšší výnos slovo zdánlivě zcela záměrně. Mnohdy, použije-li každý hráč dominantní strategii – tedy zachová-li se sobecky, výsledný výnos pro všechny může být nakonec nižší [1].

Tím se dostáváme k tomu, že teorie her vysvětluje i to, proč je lepší chovat se spíše kooperativně než sobecky. Klasickým příkladem jsou cenové kartelové dohody dominantních dodavatelů některého zboží, které jsou větším přínosem pro jednotlivé hráče než cenová válka, kdy se předhánějí, kdo prodá zboží levněji. V konečném důsledku by to znamenalo – dovedeno do absurdnosti – nulové zisky pro každého z nich. Pouze krátkozraký hráč si může myslet, že bude prodávat za nižší cenu než jeho soupeř po dlouhou dobu a nakonec oba dostanou rozum. Druhou věcí je, že jakékoliv dohody kontroluje – tu s větším tu s menším úspěchem – antimonopolní regulátor, skutečností však zůstává, že přirozeností větších hráčů na trhu je nakonec se nějak dohodnout. Tak ekonomové většinou vysvětlují jev strnulých či neklesajících cen právě pomocí teorie her.

Dalším zlatým standardem příkladu kooperativního chování je tzv. vězňovo dilema, kdy pro dva vězně, odděleně vyslýchané pro stejný čin, je lepší mlčet a vzájemně se tedy podporovat, než se přiznat za příslib nižšího trestu pro udavače, a naopak vyššího trestu pro toho, kdo by mlčel. Pokud jeden druhému nevěří, že bude ten druhý také mlčet, promluví raději oba a výsledkem bude, že dostane každý z nich nakonec vyšší trest než v případě kooperativního nevypovídání.

Výzkumy ukazují, že pokud se hra typu vězňovo dilema stále znovu opakuje, je rozumné, aby se lidé chovali kooperativně a často se také kooperativně chovají právě na bázi strategie „jak ty mně, tak já  tobě a v budoucnu zase naopak“. Je to tedy nejprospěšnější dominantní strategie v mnoha opakovaných hrách typu vězňovo dilema. Ostražité zlaté pravidlo může lidem dobře posloužit v mnoha situacích: „Chovej se k jiným tak, jak chceš, aby se oni chovali k tobě, ale pouze tak dlouho, dokud jednají tak, jak jednáš ty“ [3].

Společným jmenovatelem situací typu vězňovo dilema je rozpor mezi úzkým soukromým zájmem a širšími zájmy většího společenství. Volba, která je přitažlivější z hlediska jednotlivce, je méně přitažlivá z pohledu celé skupiny [1]. Pro úplnost uvádím, že v životě se častěji setkáváme s typem her, v němž hraje roli správné načasování (kuj železo, dokud je žhavé), či her s ultimátem (když ty uděláš-neuděláš, pak já udělám-neudělám), kdy lepší než výherní matice hry je stanovit strategii pomocí tzv. rozhodovacího stromu. Tento strom popisuje možné tahy soupeře v pořadí, v jakém se během hry vyskytnou a uvádí výsledné zisky pro libovolnou kombinací tahů. Mnohé negociace či vyjednávání se hrají podle pravidel moje akce – protihráčovy možné reakce (co se asi nejpravděpodobněji stane, když...).

Dennodenně se tak každý z nás větší či menší měrou účastní na první pohled neviditelné hry. Pravidla jsou jak psaná – v zákonech a vyhláškách, tak i nepsaná – daná zvyky, tradicí, kulturou.

V reálném světě se většinou vyskytují hry s tzv. nenulovým součtem (v podnikání, politice, příkladem může být tzv. vězňovo dillema), kdy některé výsledky přinášejí celkový čistý užitek větší nebo menší než nula. Neboli zisk jednoho hráče nemusí pro jiného hráče nutně znamenat ztrátu.

Obecně naše chování (a jeho motivy) osciluje mezi restrikcí a motivací – mezi legislativními limity a hrozbami trestu za jejich neplnění a individuální motivací případné odměny za určité chování.

Lékařovo dilema

Aplikujeme-li teorii her do konkrétní situace, kterou jsem nazval „lékařovo dilema“, pak hráči jsou v naší pomyslné hře tři:

1. zadavatel,
2. posudkový lékař jako plnitel zadání,
3. posuzovaný.

Hraje se modifikovaná hra víceméně s nenulovým součtem, a navíc s načasováním a ultimátem. Jakkoliv není tímto klasická výherní matice dost dobře aplikovatelná (spíše je na místě rozhodovací strom, protože se hráči v tazích střídají), pro jednoduchost jsem ji nakonec použil. Nastává tu pouze situace všechno nebo nic, tedy přiznáno-nepřiznáno. A následuje podle akce jedné strany protiakce strany druhé (nepřiznám – protistrana se odvolá – já nějak pokračuji – protistrana také atd.).

Motivace posuzovaného je jasná. Již v roce 1513 napsal Niccolo Machiavelli ve svém Vladaři: „Panovník si respekt udrží, dokud nesáhne poddaným na majetek a na jejich ženy. Lidé spíš zapomenou na smrt třeba i vlastního otce než na ztrátu majetku.“ Totéž platí o mezilidských vztazích, smír končí, pokud jsou ve hře výhody, respektive majetek. Přirozenost člověka je přece daná geneticky a je krutě sobecká. Posudkový lékař je ten, kdo rozhoduje o materiálních výhodách, chcete-li o navýšení majetku posuzovaného. Je branou i překážkou.

Druhý hráč – zadavatel – je úřad, státní, obecní. Pominu to, že ze samé podstaty je to množina lidí byrokraticky hierarchizovaná, s různými zájmy a potřebami. Zjednodušeně, jako právnická osoba má tento zadavatel jako plátce výhod zájem tyto výhody dát adresně a korektně potřebným občanům.

Tím třetím hráčem jsme my, posudkoví lékaři. V praxi se pochopitelně jedná o souboj dvou hráčů, protože zadavatel deleguje své potřeby na posudkového lékaře. Jaký výsledek – součet této hry by měl být? Laboratorně vzato – asi nulový. To by platilo za následujících podmínek: Pacient buď dostane, nebo nedostane výhodu, u něj je tedy matematicky dáno: výhra (+1) dostanu, prohra (-1) nedostanu; u posudkového lékaře naopak, dá výhodu, tedy (-1), nebo-li prohra, nedá výhodu (+1) tedy výhra. Výsledek je vždy tentýž: na jedné straně výhra (+1), na straně druhé prohra (-1). Tedy (+1) + (-1) = 0. Je však pro lékaře dát výhodu jednoznačně prohra a nedat výhodu je výhra? V praxi to přece není a nemůže být tak jednoduché. Nepodobá se spíše realitě tento výsledek:

A. Posudkový lékař přizná

Posuzovaný – výhra, výsledek = (+1)

Posudkový lékař – škála od pozitivního pocitu (snížil handicap posuzovaného, zmírnil jeho problémy) do neutrálního pocitu (není nikterak ekonomicky zainteresován na ušetřených státních prostředcích, leda virtuálně jako loajální úředník a občan) – záměrně se zde vyhýbám sportovní terminologii výhra (pozitivní pocit), respektive remíza (neutrální pocit).

Parciální výsledek = (+1) nebo (0)

Konečný výsledek hry: posudkový lékař vyhovuje = (+2) nebo (+1) tedy pozitivní.

B. Posudkový lékař nepřizná

Posuzovaný – jednoznačná prohra, využije všech legálních prostředků, aby se dovolal svého práva, vystupuje tedy jako soukromá osoba používající veškerou dominantní strategii vedoucí k jeho zisku, nemá zájem ušetřit státní prostředky. Je osobně zainteresován na výsledku. O jeho osobní výhody se hraje.

Parciální výsledek = (-1)

Posudkový lékař – škála od neutrálního pocitu (opět platí – jako lékař se neraduje prvotně z toho, že ušetřil státní prostředky, protože vždy zpytuje svědomí, zda neublížil pacientovi, tvrdě trvaje na ne vždy jednoznačných posudkových kritériích) až po vysloveně negativní pocit a následky svého rozhodnutí (útoky ze strany posuzovaného typu právní kroky až negativní medializace lékařovy osoby). Opět záměrně se vyhýbám slovům remíza (neutrální pocit), respektive prohra (negativní pocit). Na výsledku je zainteresován jen jako zaměstnanec, neosobně.

Parciální výsledek = (0) nebo (-1)

Konečný výsledek hry: posudkový lékař nevyhovuje = (-1) nebo (-2), tedy negativní.

Graficky vyjádřený výsledek – obrázek 1.

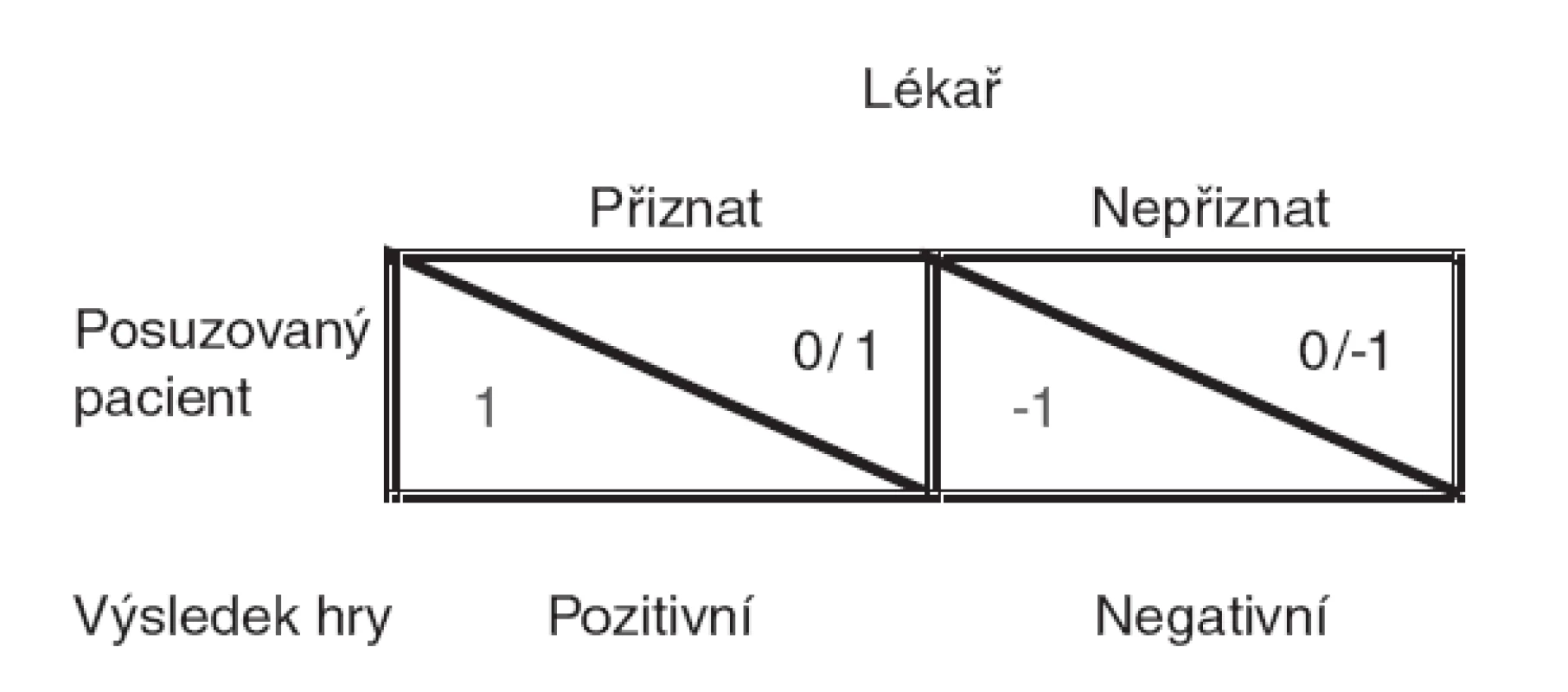
Je to příliš zjednodušeně odvážná zkratka motivace našeho chování jako posudkových lékařů? Nezmínil jsem se o faktoru, kterým bych měl v úvaze nad motivací posudkového lékaře začít, a to je faktor, proč se za současných podmínek lékař vůbec stane posudkovým, do hry by pak vstoupily i jeho základní morální a volní vlastnosti, jeho životní peripetie a zkušenosti, jeho ego i míra altruismu. To by však znamenalo celý tento článek zrelativizovat a posunout od matematiky a její teorie her do vod sociologie a filozofie.

Chtěl jsem vnést jen otázky do diskuse, nakolik jsme ještě ortodoxními lékaři a nakolik již zdravotními soudci. A jaké výsledky našich posudků jsou možné z pohledu aplikované matematiky. Nabízí se zde otázka, jak by nastíněná výsledková matice fungovala na jiném formátu – privatizací posudkové služby? Nakolik by se změnila motivace posudkového lékaře, který by vystupoval v této hře s přenesenou pravomocí státu nebo obce, ne jako zapomenutelný zaměstnanec, ale jako viditelný a vážený licencovaný odborník svým jménem a na svůj účet vykonávající svobodné povolání?

Nakolik by se bál tento lékař případné ztráty licence a živobytí, kdyby plnil více tu první roli ochránce pacientů než tu druhou roli nekompromisního soudce? Zlepšila by se prestiž tohoto oboru? Hrnuli by se noví zájemci o tuto činnost tak, že by počet těchto „zdravotních notářů“ byl regulátorem limitován podobně, jako zdravotní pojišťovny nekompromisně regulují nové smlouvy se zdravotnickými subjekty? A stali by se z kolegů najednou konkurenční dravci?

A je zde vůbec nějaká vůle tyto otázky otevřít a řešit? Skončím raději jednou zásadní myšlenkou. Liberální skotský ekonom a filozof Adam Smith ve svém stěžejním díle Pojednání o podstatě a původu bohatství národů (An Inquiry into the Nature and Causes of the Wealth of Nations ) již v roce 1776 píše slavný výrok: „ Každý jednotlivec se snaží použít svůj kapitál tak, aby jeho produkt měl co největší hodnotu. Obvykle nezamýšlí prosadit veřejný zájem, a ani neví, do jaké míry ho prosazuje. Sleduje pouze své vlastní zabezpečení, pouze svůj vlastní prospěch. Přitom ho vede jakási neviditelná ruka, aby prosazoval cíl, o který mu vůbec nešlo. Sledováním svého vlastního zájmu často prosazuje zájem společnosti účinněji, než když ho opravdu zamýšlí prosadit.”

Adresa pro korespondenci:

MUDr. Miroslav Bílek

Oblá 42

634 00 Brno