Makrodesign implantátu – typy a tvary používaných závitů a jejich hodnocení metodou konečných prvků

Souhrn

Úvod a cíl práce:
Mechanický přenos zatížení na kost ovlivňuje kromě materiálových vlastností implantátu (mikrodesign), zejména typ použitého závitu a jeho parametry (makrodesign). Rozeznáváme čtyři základní tvary závitů: a) metrický, b) plochý, c) pilovitý, d) obrácený pilovitý a dva modifikované tvary podle ISO TC 150 normy: e) ISO Shallow HA kortikální a f) ISO Deep HB spongiózní. Mechanický přenos charakterizuje míru přenosu mechanického napětí ze závitu do kosti a je menší než jedna. V ideálním případě je roven jedné, ale vlivem odlišné pevnosti a pružnosti kosti a materiálu závitu je obtížné této hodnoty dosáhnout. Byly stanoveny dva cíle studie. Prvním bylo zjistit rozložení napjatosti (tj. tlakového, tahového a smykového napětí) nejčastěji používaných typů závitů zubních implantátů na rozhraní implantát – kost. Druhým cílem byl popis mechanické kompatibility (čili mechanického přenosu zatížení z implantátu na okolní kost) u stejných typů závitů.

Metody:
Pro modelování vlivu tvaru závitu implantátu na rozložení napětí v místě rozhraní implantát – kost jsme použili metodu konečných prvků v programu MSC Marc (MSC Software s.r.o., ČR) a metodiku podle Gefena, při které jsme analýze podrobili celou délku kontaktu implantátu s kostí.

1. Definování okrajových podmínek. Velikost zatěžující síly byla F = 100 N, směr síly byl totožný s dlouhou osou implantátu a působiště síly bylo v jeho krčkové části.
2. Charakterizování materiálového modelu. K popisu materiálových vlastností kosti jsme použili izotropní model, který definují dvě konstanty: Youngův modul pružnosti (E) a Poissonovo číslo (μ).
3. Definování typu úlohy. Model byl simulován jako prostorová osově symetrická úloha.

Výsledky:
Z hlediska tahového napětí se ukazuje jako nejlepší závit ISO Shallow HA, v případě tlakového a smykového napětí se jeví nejvhodnějším plochý závit. Výsledky spočítané metodou konečných prvků u všech typů simulovaných závitů potvrzují, že v závitovém spojení je největší podíl napětí soustředěn v prvních cervikálních závitech.

Diskuse a závěr:
Z provedených simulací plyne, že profil závitu hraje významnou roli v ovlivnění velikosti a rozložení napětí v okolní kosti a mechanické kompatibility. Naše matematická studie neprokazuje, že existuje jeden ideální závit pro dentální implantát.

Klíčová slova:
dentální implantát – design – závit – napětí – mechanická kompatibilita – analýza konečných prvků

ÚVOD

Dentální implantáty jsou součástí moderní stomatologie a výrobci se snaží v jejich designu reflektovat nejnovější vědecké poznatky. Z makrodesignového hlediska jde především o zvýšení mechanické kompatibility (čili zajištění nejvhodnějšího mechanického přenosu zatížení z implantátu na okolní kost), a tím odstranění nežádoucího „stress shielding“ efektu. Poprvé byl tento efekt pozorován u kyčelních náhrad a jde o reakci okolní kosti na mechanické stimuly. Je zřejmé, že zvýšené zatížení rozhraní implantát – kost („stress shielding“) má za následek častější uvolnění implantátu, jeho kratší životnost a horší dlouhodobý výsledek. Protože tuhost implantátu je řádově vyšší než tuhost okolní tkáně, ovlivňuje tento rozdíl negativně mechanickou kompatibilitu.

K popisu napjatosti se používají tři druhy mechanického napětí na rozhraní implantát – kost. Je to napětí tahové, tlakové a smykové. Jak velké napětí ale v kosti nakonec vznikne, závisí na tom, kolik zatížení se přenese z implantátu do okolních tkání. Již v roce 1892 Wolff [15] popisuje změny, které jsou vyvolány ve struktuře kostí vnějšími silami: „Každá změna ve funkci a formě kosti vede k nevratným změnám v interní struktuře kosti samotné.“ Nejdůležitější součástí tohoto zákona je hypotéza o trajektorii a adaptačním modelování. Hypotéza o trajektorii popisuje shodu uspořádání trámčité struktury kosti s rozložením izoploch výsledného napětí, pod pojmem adaptační modelování chápeme změny tvaru a struktury kosti v důsledku působení vnějších sil.

Kromě materiálových vlastností implantátu je mechanický přenos zatížení ovlivněn také typem a parametry použitého závitu. Rozeznáváme čtyři základní tvary závitů: a) metrický, b) plochý, c) pilovitý, d) obrácený pilovitý a dva modifikované tvary podle ISO TC 150 normy [17]: e) ISO Shallow HA kortikální a f) ISO Deep HB spongiózní (obr. 1).

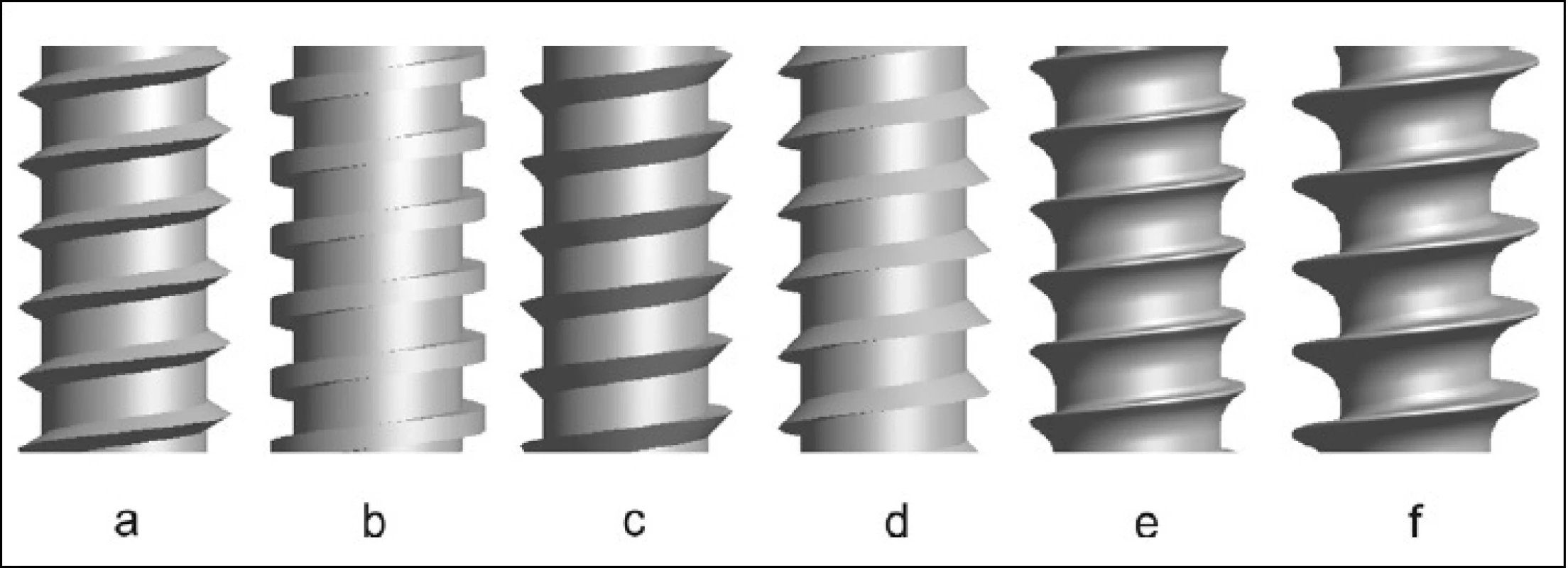
• a) Metrický závit je obecně nejčastěji používaným závitem s vrcholovým úhlem 60 stupňů. Rozeznáváme závit s hrubou a jemnou roztečí, přičemž jemný závit je odolnější vůči vibracím.
• b) Plochý závit má profil ve tvaru čtverce a nejčastěji se používá v posuvném vedení. Výhodou závitu je jeho vysoká mechanická účinnost, velkou nevýhodou je jeho výrazně dražší výrobní technologie.
• c) Pilovitý závit je používán zejména pro posuvná vedení, která musí přenášet velké síly v jednom směru.
• d) Obrácený pilovitý závit se liší od závitu pilovitého pouze orientací čela závitu.
• e) ISO Shallow HA je speciálně navržen pro kortikální kost.
• f) ISO Deep HB je designován pro spongiózní kost.

Mezi základní charakteristiky závitu řadíme: a) hloubku závitu, b) šířku závitu, c) rozteč závitu (obr. 2) a stoupání závitu.

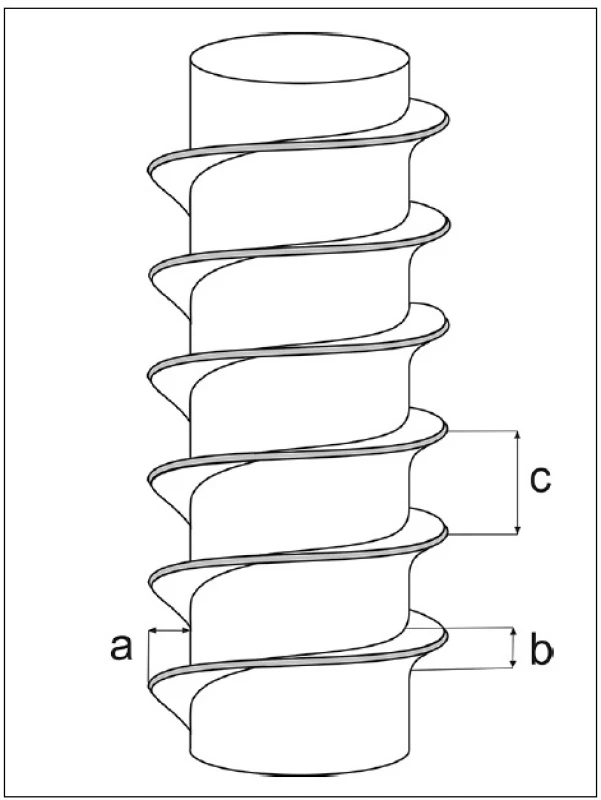
• a) Hloubka je dána rozdílem vnitřního a vnějšího průměru závitu a s její velikostí roste kontaktní plocha pro přenášení mechanického zatížení do kosti.
• b) Šířka závitu je definována jako vzdálenost měřená na protilehlých stranách závitu v osovém řezu. V případech nekonstantní šířky závitu se její rozměr měří na středním průměru závitu nebo na jiném, vhodně definovaném průměru.
• c) Rozteč závitu udává vzdálenost mezi dvěma závity měřenou na stejně orientovaných plochách závitu.

Stoupání závitu vyjadřuje vztah mezi otočením implantátu o 360 stupňů a výsledným apikálním posuvem. Existují implantáty, jež obsahují závitová vlákna tak, že otočení o 360 stupňů není rovno rozteči závitu, ale jejímu násobku. Podle toho se implantáty dělí na jednoduché, dvojzávitové a trojzávitové (obr. 3). Tento údaj nekvalifikuje implantát z hlediska počtu závitů, ale z hlediska úhlu stoupání.

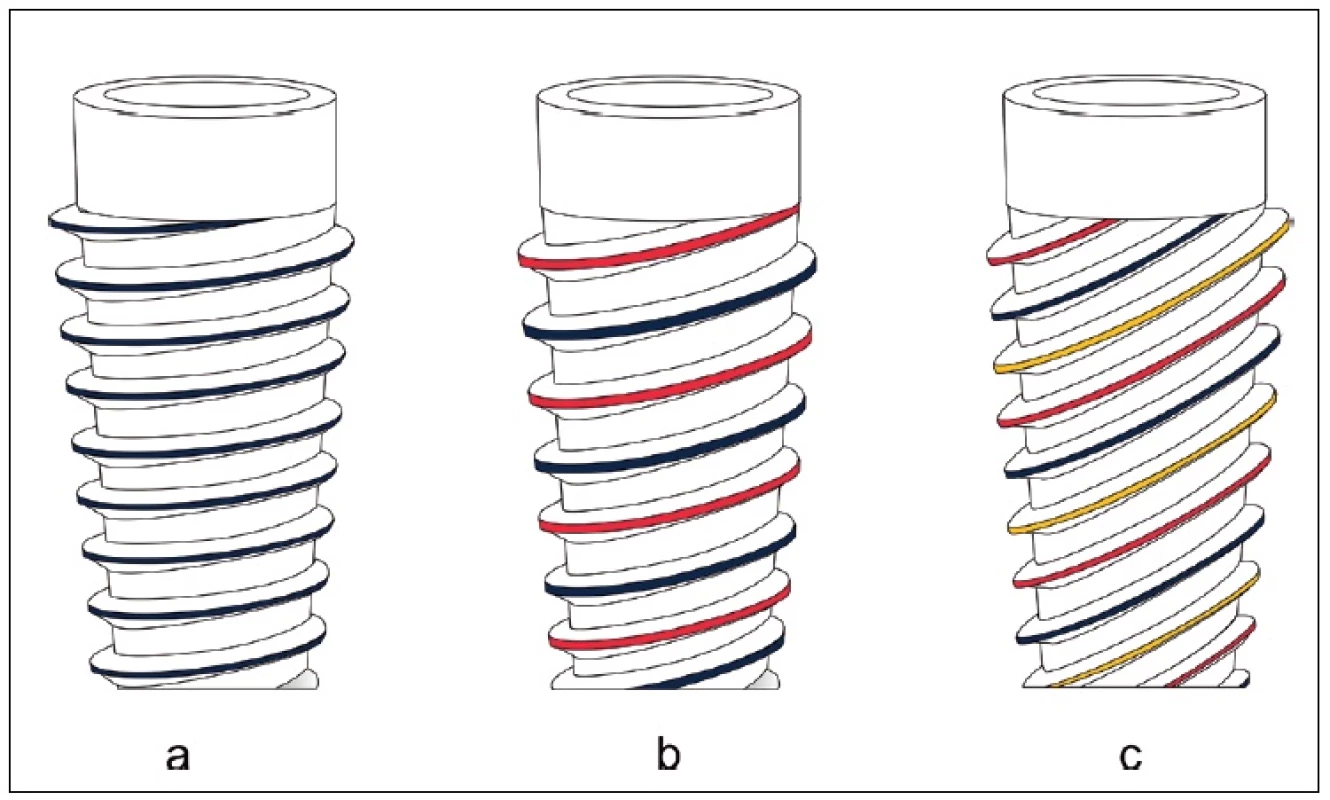
Vztahem mezi parametry závitu a rozložením intenzity napětí v kosti se dnes zabývá řada studií a ve většině případů je k posouzení tohoto vztahu použita metoda konečných prvků [1, 3–14, 16]. Obecně se doporučuje přizpůsobit hloubku závitu implantátu hustotě okolní kosti. V apikální části je proto ideálnější hlubší závit, který jde snadno zavést do spongiózní kosti, v oblasti kortikální kosti se doporučuje implantát opatřit mělkým závitem. Využitím vhodného typu závitu při návrhu dentálního implantátu lze zvýšit stabilitu implantátu a zvětšit kontaktní plochu mezi kostí a implantátem. Hansson a Werke [3] provedli analýzu tvaru závitu na rozložení napětí pomocí jeho standardizovaných rozměrů. Uvádějí, že jemné závitové spojení je efektivnější než hrubé závitové spojení. Lee a kol. [9] se zabývali rozložením kontaktní plochy a napětí pro metrický, čtvercový a pilovitý závit. Největší kontaktní plocha vzniká u čtvercového závitu, následuje pilovitý a metrický závit. Při shodných parametrech závitů (rozteč 0,8 mm) je kontaktní plocha pilovitého závitu o 3,76 % menší než u čtvercového závitu a plocha metrického závitu je o 7,52 % menší než u čtvercového závitu. S rostoucí kontaktní plochou klesá napětí na rozhraní implantátu a kosti.

Ao a kol. [1] provedli senzitivní analýzu při zatížení v dlouhé ose implantátu. Cílem bylo nalézt nejvhodnější hloubku (analyzovali její rozměry od 0,20 mm do 0,60 mm) a šířku závitu (rozmezí bylo od 0,10 mm do 0,40 mm) s konstantní roztečí 0,80 mm. Vypočítali, že při axiálním zatížení je optimální hodnota hloubky závitu implantátu podle typu kosti rozdílná. Pro kortikální kost je ≤ 0,23 mm nebo ≥ 0,42 mm. Pro spongiózní kost platí, že ideální hloubka závitu je ≥ 0,40 mm. Optimální hodnota šířky závitu pro kortikální kost je ≤ 0,23 mm nebo ≥ 0,34 mm. Pro spongiózní kost platí, že ideální hodnota šířky závitu je ≤ 0,23 mm nebo ≥ 0,37 mm. Jako jednoznačný výsledek prezentují to, že hloubka závitu ovlivňuje mechanickou kompatibilitu více než jeho šířka.

Kong a kol. [7] provedli analýzu vlivu rozteče závitu na koncentraci napětí. Zjistili, že na změnu rozteče více reaguje spongiózní kost než kost kompaktní. Ideální poměr mezi primární stabilitou a úrovní napětí v kosti je podle autorů při hodnotách rozteče 0,75 až 0,8 mm. Její vliv se ukázal zejména v oblasti spongiózní kosti, kdy je možno docílit vhodnou volbou zmenšení napětí až o 55,2 % při axiálním zatížení a až o 22,4 % v případě bukolingválního zatížení. Ma a kol. [11] porovnávali různé úhly stoupání závitů při jejich shodné rozteči 0,8 mm. Z hlediska primární stability se ukázalo, že nejvhodnější je implantát s jednoduchým závitem. Jako nejhorší se pak jevilo trojzávitové řešení. Merdji a kol. [13] ve shodě se všemi autory poukazují, že rovněž směr zatížení má významný vliv na rozložení napjatosti v implantátu a kosti.

Výsledky dostupných studií tedy potvrzují, že rozložení napětí v kosti lze do značné míry ovlivnit materiálovými vlastnostmi a parametry závitu, ale zatím se nepodařilo najít ideální metodiku pro určení míry mechanické kompatibility. Z hlediska dentální implantologie je nejbližší studie Gefena [2], který zjišťoval poměr mezi mechanickým napětím vznikajícím v kosti a v ortopedickém šroubu. Pro měření si vybral korespondující body na rozhraní implantát – kost a zjištěné hodnoty napětí dal do vzájemného poměru, který nazval mechanický přenos. Tato veličina tedy charakterizuje míru přenosu mechanického napětí ze závitu do kosti a je menší než jedna. V ideálním případě je rovna jedné, ale vlivem odlišné pevnosti a pružnosti kosti a materiálu závitu je obtížné této hodnoty dosáhnout.

Byly stanoveny dva cíle studie. Prvním bylo zjistit rozložení napjatosti (tj. tlakového, tahového a smykového napětí) nejčastěji používaných typů závitů zubních implantátů na rozhraní implantát – kost. Druhým cílem byl popis mechanické kompatibility (čili mechanického přenosu zatížení z implantátu na okolní kost) u stejných typů závitů.

METODY

K popisu interakce na rozhraní implantát – kost byla vybrána veličina mechanické napětí a k analýze této interakce bylo zvoleno napětí smykové a normálové. Normálové napětí je popisováno jednou hodnotou nezávislou na směru měření a je charakterizováno tlakovým a tahovým napětím. Výstupem těchto analýz jsou tři druhy mechanického napětí: tlakové, tahové a smykové (obr. 4).

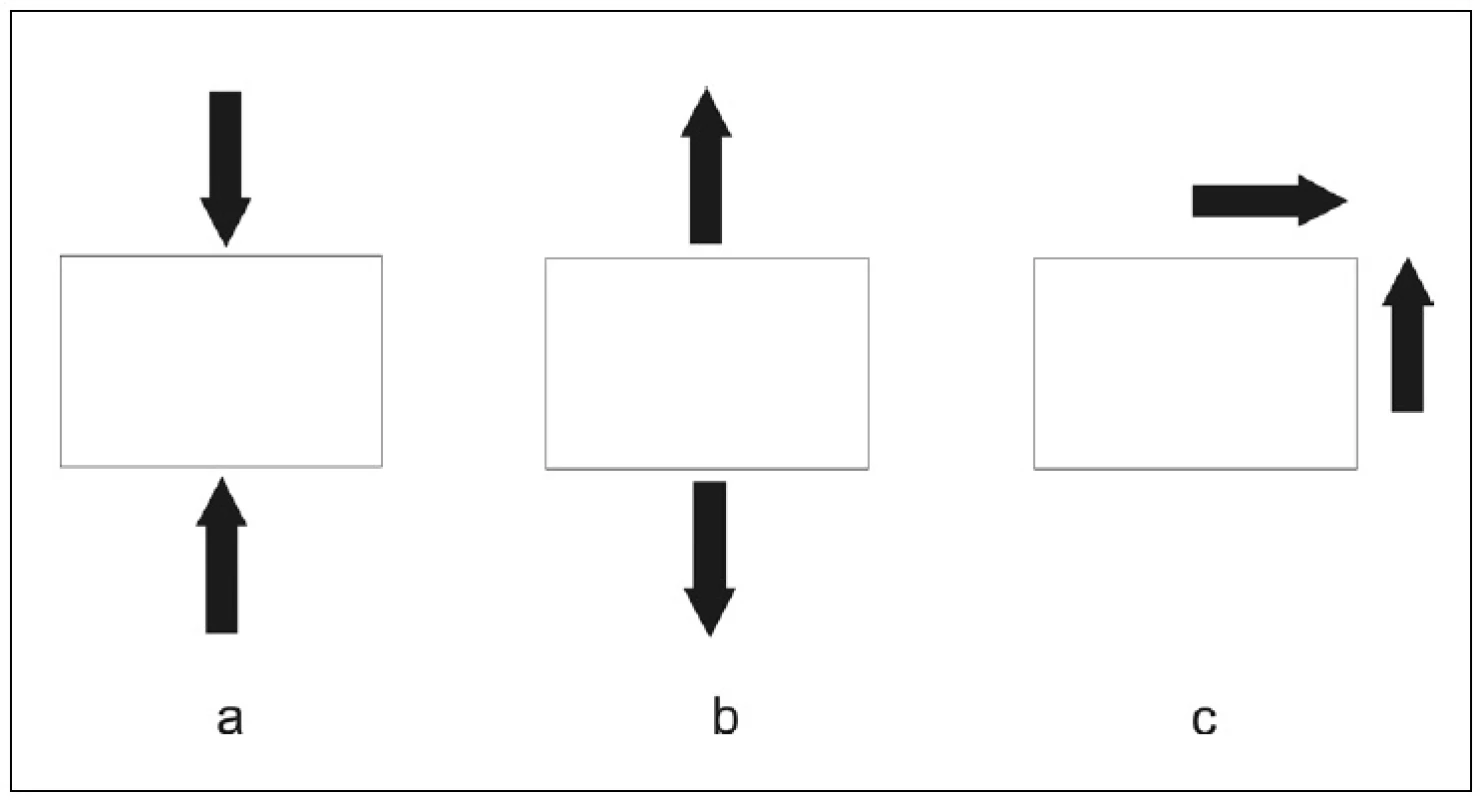
Ke zjištění mechanického přenosu z implantátu na okolní kost (míry mechanické kompatibility) jsme modifikovali metodiku použitou Gefenem [2]. Analýze jsme podrobili celou délku kontaktu implantátu s kostí (obr. 5). Celkem bylo identifikováno 270 bodů (na 1 mm délky řezu rozhraní implantát – kost připadá 10 bodů) a poměr napětí v implantátu a kosti byl následně stanoven podle vzorce:

kde α značí mechanický přenos, σ kost je normálové napětí v kosti a σ implantát je normálové napětí v implantátu.

Pro modelování vlivu tvaru závitu implantátu na rozložení napětí v místě rozhraní implantát – kost jsme použili metodu konečných prvků v programu MSC Marc (MSC Software s.r.o., ČR).

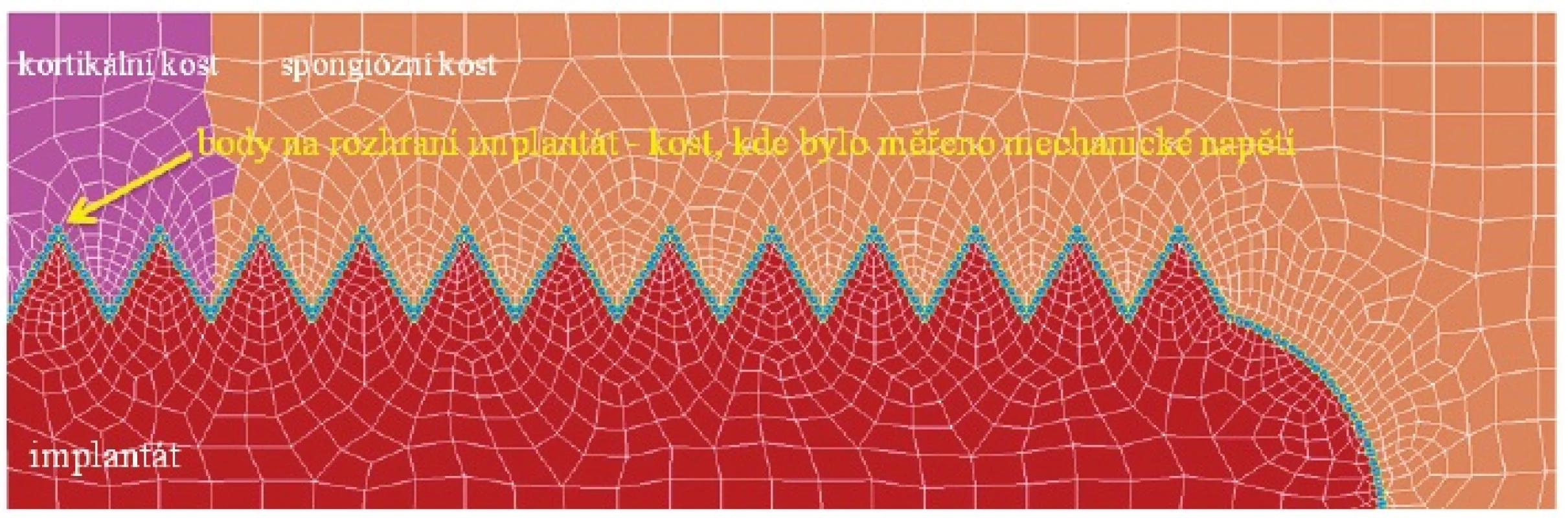
Proces vytváření modelu se skládá ze tří kroků.

1. Definování okrajových podmínek. Velikost zatěžující síly byla F = 100 N, směr síly byl totožný s dlouhou osou implantátu a působiště síly bylo v jeho krčkové části. Virtuální segment mandibuly s implantátem byl vyjmut a fixován na bočních plochách proti pohybu. Byly definovány kontaktní podmínky jednak mezi kortikální a spongiózní kostí (jde o typ nerozdělitelného spojení), dále pak mezi implantátem a kortikální a spongiózní kostí (typ spojení, při kterém se implantát vůči kosti může pohybovat).
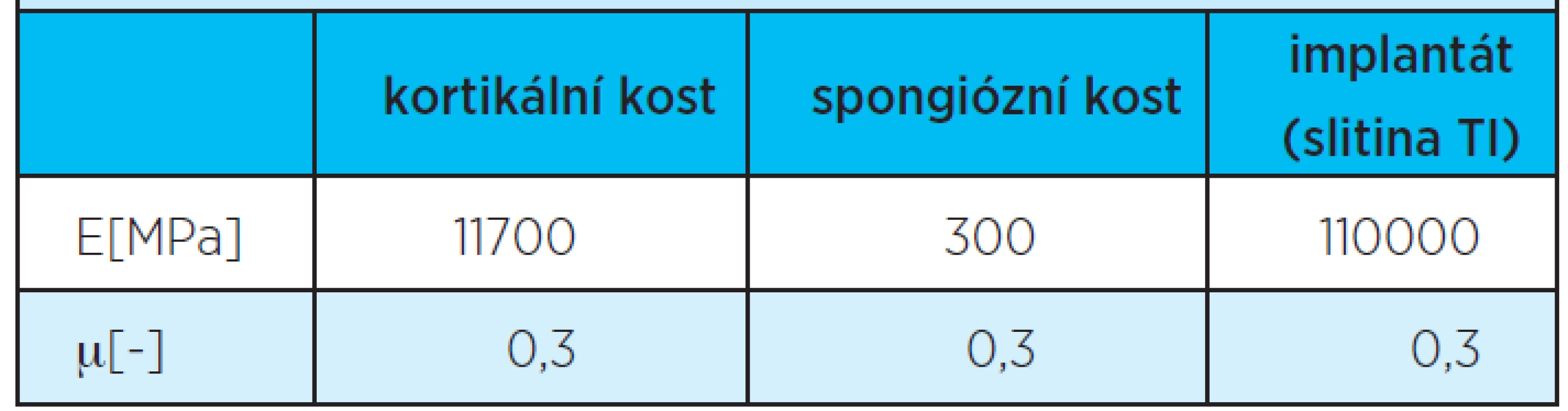
2. Charakterizování materiálového modelu. Protože kost má v každém zvoleném směru jiné materiálové vlastnosti, které jsou současnými metodami obtížně měřitelné, použili jsme k jejímu popisu izotropní model kosti, který definují dvě konstanty (tab. 1):
   • Youngův modul pružnosti (E),
   • Poissonovo číslo (µ).
3. Definování typu úlohy. Model byl simulován jako prostorová osově symetrická úloha.

VÝSLEDKY

Ideální závit je takový, který souběžně způsobuje v kosti na rozhraní implantát – kost nejmenší tahové, tlakové a smykové napětí. V tabulce 2 jsou srovnány typy závitů podle naměřených hodnot jednotlivých napětí. Z hlediska tahového napětí se ukazuje jako nejlepší závit ISO Shallow HA, v případě tlakového a smykového napětí se jeví nejvhodnějším plochý závit.

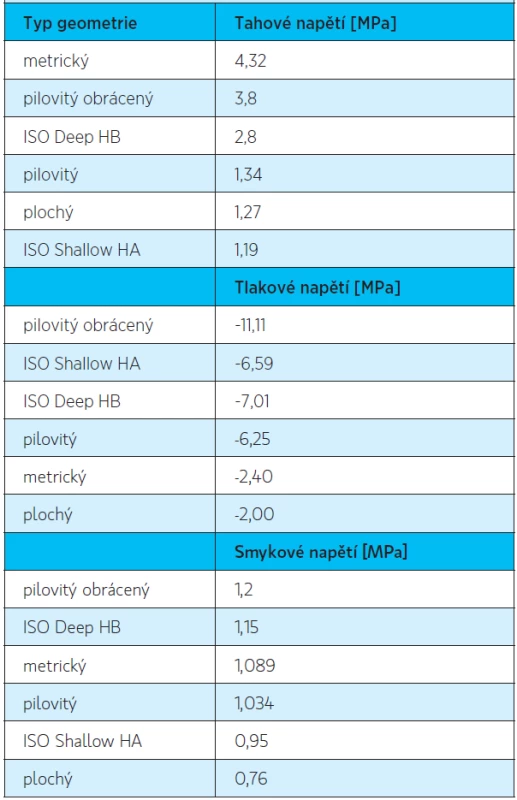
Na grafu 1 je znázorněn průběh změřeného normálového napětí kosti na jejím rozhraní s implantátem a každému typu závitu je přiřazena barevně korespondující křivka. Je obecně známo, že v závitovém spojení je největší podíl napětí soustředěn v prvních závitech, což potvrzují námi získané průběhy napětí spočítané metodou konečných prvků u všech typů simulovaných závitů.

Vliv tvaru závitu na přenos napětí na rozhraní implantát – kost byl dále zkoumán pomocí upravené metody původně navržené Gefenem [2]. Na grafu 2 jsou znázorněny průběhy mechanických přenosů jednotlivých tvarů závitů. V ideálním případě je přenos roven jedné, ale žádný závit této hodnoty nedosahuje. Z grafu je dále vidět, že v oblasti prvních závitů se vzdaluje hodnota mechanického přenosu od ideální hodnoty nejvíce. Z toho vyvozujeme, že nejhorší mechanická kompatibilita je právě v oblasti prvních závitů, kde jsou největší napěťové špičky.

DISKUSE A ZÁVĚR

Námi zkoumané profily byly seřazeny podle velikosti maximálního napětí, které přenášely do kosti při zatížení v dlouhé ose (tab. 2). Domnívali jsme se, že se nám podaří nalézt jeden ideální typ závitu. Během zatížení v dlouhé ose implantátu převažuje tahové a tlakové napětí nad napětím smykovým, které může být až o řád menší. Při porovnání z hlediska tahového se jeví jako nejlepší pilovitý kortikální profil ISO Shallow HA a jako nejméně vhodný vychází metrický závit. Z hlediska tlakového napětí je nejvhodnější profil plochý, naopak jako nejméně vhodný vychází obrácený pilovitý. Hodnoty smykového napětí na rozhraní implantát – kost u všech typů závitů byly v úzkém rozpětí od 0,76 MPa do 1,2 Mpa, a tudíž z hlediska posouzení nejvhodnějšího typu závitu nepoužitelné.

Z pohledu mechaniky závitového spojení je známo, že největší mechanická napětí vznikají v oblasti prvních cervikálních závitů. Tento fakt je v osteologii podpořen také tím, že kortikální kost má Youngův modul pružnosti E = 13 700 MPa a může být až o řád vyšší než u spongiózní kosti, jejíž Youngův modul pružnosti v průměru činí asi 300 MPa. Z toho vyplývá, že při stejném zatížení dochází k většímu napětí na rozhraní implantát – kost v kortikální části než v části spongiózní, kde je jeho průběh bez výraznějších napěťových špiček (graf 1).

Z našich výsledků je zřejmé, že pro případ zatížení implantátu v dlouhé ose není možno stanovit jednoznačně nejvhodnější profil závitu. Z naměřených hodnot jako relativně nejvhodnější vychází implantát s plochým profilem závitu, ale jeho výroba je výrazně nákladnější než u ostatních typů závitů. Tuto nevýhodu nevyváží získaná redukce napětí, která není extrémně výraznější ve srovnání s ostatními typy.

Dalším kritériem hodnocení závitů implantátů byla modifikovaná metoda navržená Gefenem [2]. Její pomocí jsme získali představu o vývoji mechanické kompatibility na rozhraní implantát – kost. Ideálním výsledkem je mít vysokou mechanickou kompatibilitu a současně dostatečně velké mechanické napětí v kosti. V kritické části rozhraní implantát – kost (první dva až tři závity) je mechanická kompatibilita nízká, ale mechanické napětí vysoké. Je zřejmé, že vysoké napěťové špičky negativně ovlivňují mechanickou kompatibilitu.

Ideálním stavem je tedy existence takového poměru mechanického napětí a kompatibility na rozhraní implantát – kost, který zajistí dostatečnou primární stabilitu. Ta charakterizuje, jak pevně je implantát zaveden do kostního lože. Pokud je implantát nestabilní, nepůsobí na rozhraní implantát – kost téměř žádná síla, která by pohybu bránila. To znamená, že na rozhraní není přítomno mechanické napětí, které je podmínkou pro existenci primární stability.

Z provedených simulací plyne, že profil závitu hraje významnou roli v ovlivnění velikosti a rozložení napětí v okolní kosti a mechanické kompatibility, ale matematická studie neprokazuje, že existuje jeden ideální závit pro dentální implantát. Bylo by nutné provést řadu podobných studií in vivo, ale takové experimenty jsou finančně a technicky velice náročné a závěry by se nejspíše významně nelišily od výsledků získaných pomocí matematických modelů.

Domníváme se, že posuzování kvality mechanického přenosu může být cenným pomocníkem při návrhu nebo optimalizaci celkového profilu implantátu.

Prim. MUDr. Ladislav Dzan

Oddělení ústní, čelistní a obličejové chirurgie

KN Liberec, a.s.

Husova 10

460 63 Liberec 1

e-mail: ladislav.dzan@seznam.cz