Analýza dat v neurologii.
XXVII. Hodnocení diagnostických testů – vliv prevalence nemoci

V tomto díle seriálu se budeme dále věnovat diagnostickým testům, které mohou nabývat pouze dvou hodnot (pozitivní, negativní výsledek). Navážeme na předchozí díly, kdy jsme čtenářům přiblížili hodnocení senzitivity a specificity testu, prediktivní hodnoty pozitivního a negativního testu, analýzy pomocí věrohodnostního poměru a diagnostického poměru šancí. Všechny tyto ukazatele lze spočítat na základě tabulky četností 2 × 2, kde proti sobě stojí výsledek testu a objektivní skutečnost. V závěrečné diskuzi v předchozím díle seriálu jsme tuto poněkud rozmanitou sadu analýz obhajovali jako smysluplnou, neboť různé ukazatele mají rozdílnou interpretaci a vyjadřují diagnostickou věrohodnost testu z různých pohledů.

Avšak ani sebelepší škála využitelných ukazatelů nás neochrání před rizikem zkreslení, které vyplývá z dat samotných. Mezi možnými zdroji zkreslení musíme samo­zřejmě na prvním místě jmenovat velikost vzorku. Je samozřejmé, že malé vzorky neumožní zobecnitelné hodnocení a nadto u nich výrazně roste riziko nereprezentativnosti. Dalšími faktory ovlivňujícími výsledek jsou výběr hodnocené populace a prevalence sledované choroby v populaci. Výkladu jejich vlivu se budeme věnovat v tomto díle.

Je pochopitelné, že ideální základ pro analýzu diagnostické věrohodnosti testu je soubor dat, kde by všichni jedinci (zdraví i nemocní) byli vybráni zcela náhodným způsobem z cílové populace. Bohužel je v praxi mnohem častější, že máme k dispozici již předem danou skupinu nemocných a zdravých jedinců a u nich provedeme daný test. V této situaci jsou využitelné výpočty senzitivity a specificity, ale odhad prediktivní hodnoty testu může být zkreslený (tab. 1). Takto sestavený soubor dat totiž nemusí věrohodně odrážet skutečný výskyt choroby v populaci, a test je tak hodnocen v podmínkách, které neodpovídají praxi. V dalších úvahách musíme zohlednit prevalenci choroby v populaci.

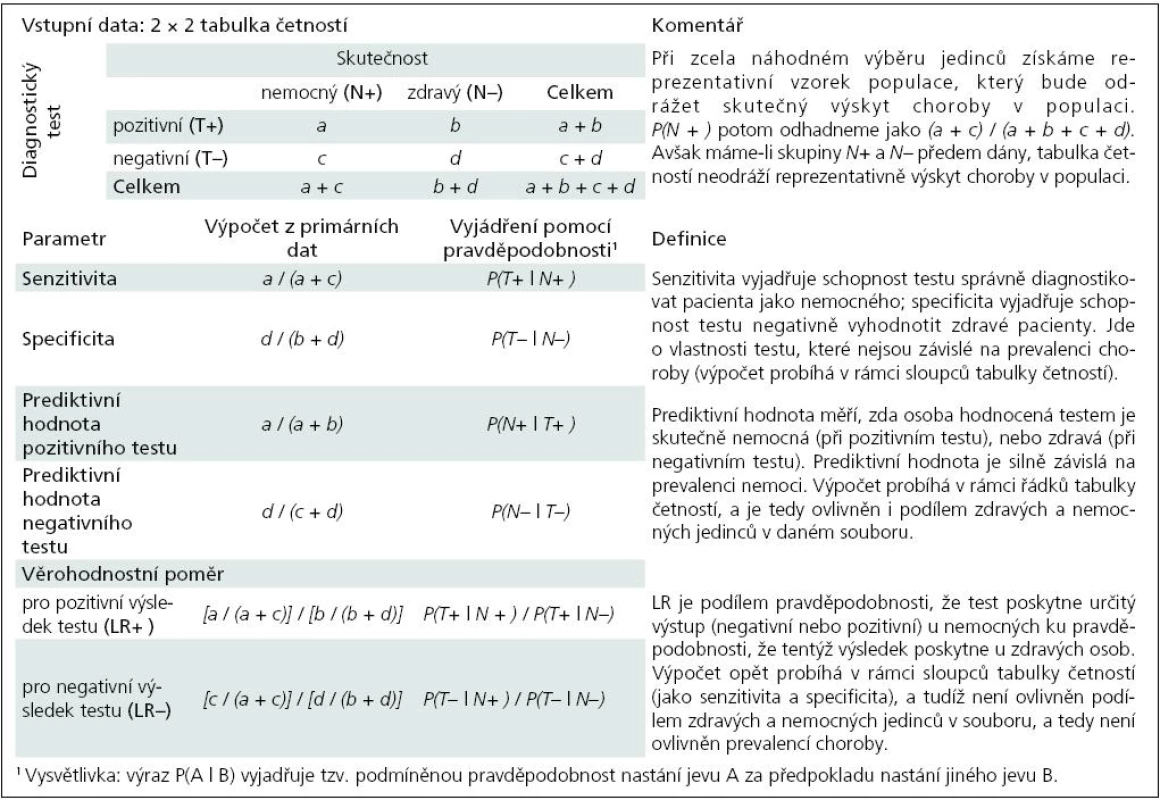
Označíme-li přítomnost nemoci N+, pak její prevalenci v populaci můžeme jednoduše definovat jako pravděpodobnost výskytu, tedy P(N+). Někdy také hovoříme o apriorní pravděpodobnosti (pre-testová pravděpodobnost, prior probability) výskytu choroby, neboť s touto pravděpodobností se choroba vyskytuje bez ohledu na aplikované diagnostické testy. Prediktivní hodnota pozitivního testu (tab. 1) naopak odhaduje pravděpodobnost záchytu choroby u osob, které prošly daným diagnostickým testem (tzv. post-testová neboli aposteriorní pravděpodobnost, posterior probability).

Prevalence nemoci ovlivňuje prediktivní hodnotu testu, tedy pravděpodobnost, že je pacient skutečně nemocný (zdravý), pokud test vyjde pozitivní (negativní). U onemocnění běžných v populaci, to je u chorob s vysokou prevalencí, můžeme logicky očekávat vyšší prediktivní hodnotu testu než u onemocnění vzácných (Harrell et al, 1982). Známe-li prevalenci choroby, můžeme vypočítat šanci pro výskyt choroby, označenou jako O(N+), a naopak ze znalosti šance vypočítat hodnotu prevalence (viz též XXVI. díl seriálu):

                 P(N+)            P(N+)
O(N+) =  ------------   =   ---------
                1–P(N+)         P(N–)

Logicky čím více prevalentní choroba je, tím větší je šance pro její výskyt. Šance výskytu choroby v populaci 1 ku 9, tedy O(N+) = 0,11 odpovídá hodnotě P(N+) = 1/10 = 0,1. Vyšší šance u jiné choroby, například 1 ku 4, zase odpovídá hodnotě prevalence P(N+) = 1/5 = 0,2.

Zatímco tedy pre-testová šance výskytu choroby souvisí pouze s její prevalencí v populaci, post-testová šance zjištění choroby musí nutně záviset i na diagnostické síle, resp. věrohodnosti testu. Díky tomuto logickému vztahu možná lépe vysvětlíme význam poměru věrohodností, neboť platí:

Post-testová šance = pre-testová šance × věrohodnostní poměr LR+

Samozřejmě usilujeme o to, aby aplikované testy zvyšovaly šanci záchytu choroby proti zcela náhodnému výběru z populace. Ve statistické terminologii tudíž preferujeme testy s co nejvyšší hodnotou věrohodnostního poměru.

Výše uvedený vztah lze komentovat následovně:

• šancí vždy myslíme „šanci pro záchyt choroby“
• je patrné, že LR+ je vlastně poměrem post-testové ku pre-testové šanci záchytu choroby, a vyjadřuje tak, kolikanásobně zvyšujeme testováním šanci, že chorobu s danou prevalencí zachytíme (poměr šancí najdeme v mezinárodní literatuře jako „odds ratio“, OR)
• je-li LR+ = 1, test nijak neovlivňuje pravděpodobnost záchytu choroby danou její prevalencí
• je-li LR+ > 1, je pozitivita testu asociována s přítomností nemoci a při LR+ < 1 je pozitivita asociována s nepřítomností nemoci.

Tab. 1 dokládá, že senzitivita a specificita jsou vlastnosti daného testu a jako takové nejsou u dichotomických výstupů testu ovlivněny prevalencí choroby. Obdobně je na prevalenci nezávislý věrohodnostní poměr, což rovněž vyplývá z výše uvedeného vztahu mezi post- a pre-testovou šancí pro záchyt nemoci. Avšak prediktivní hodnota testu na prevalenci nemoci závisí, jak dokumentuje příklad 1. Příklad pracuje s různými soubory dat, u nichž vždy vyjde stejná senzitivita a specificita diagnostického testu. Jelikož ale soubory pocházejí z populací s různou prevalencí choroby, významně se mezi nimi liší prediktivní hodnota testu. S rostoucí prevalencí onemocnění roste pozitivní prediktivní hodnota a naopak klesá negativní prediktivní hodnota testu.

Výpočet prediktivní hodnoty (PH) u testů v příkladu 1 zahrnuje prevalenci choroby pouze nepřímo, neboť si ji sám odhaduje z dat (jako celkový počet nemocných děleno celkovým počtem sledovaných osob). Jeho výpovědní hodnota se tak vztahuje vždy pouze na daný soubor dat, bez možnosti zobecnění na celou populaci v případě, že nemáme zajištěnu reprezentativnost souboru pacientů. Pokud je soubor sestaven z nereprezentativních jedinců, tedy nereprezentativních skupin nemocných a zdravých (např. jako záznamy z konkrétní kliniky), je nutné použít pro výpočet prediktivní hodnoty vztah, který zahrnuje přímo hodnotu prevalence onemocnění. Jen tak lze odhad prediktivní hodnoty testu zobecnit na cílovou populaci. Tyto vztahy jsou následující:

              senzitivita × prevalence
PH+ = ------------------------------------------------------------------------
             senzitivita × prevalence + (1–specificita) × (1–prevalence)

            specificita × (1–prevalence)
PH–  = ----------------------------------------------------------------------
           (1–senzitivita) × prevalence + specificita × (1–prevalence)

Výhodou výpočtu je jistě jeho jednoduchost. Známe-li pro daný test senzitivitu a specificitu, můžeme snadno spočítat prediktivní hodnotu pro jakoukoli prevalenci onemocnění (kterou lze dosazovat i simulačně). Další výhodou je možnost odhadovat prediktivní hodnotu testu pro různé populační skupiny, kde se prevalence onemocnění liší (např. při dělení dle věku nebo pohlaví). Takové výpočty mají v praxi velký význam např. pro nastavování cílových skupin pro různá preventivní vyšetření či plošné programy skríningu nemoci. Dokumentace výpočtu je uvedena v příkladu 2.

Tab. 2 shrnuje výše uvedené výpočty a vztahy v dalších číselných příkladech. Je patrné, jak významně prevalence nemoci ovlivňuje prediktivní hodnotu testu při různých hodnotách specificity a senzitivity. Například test s 95% senzitivitou a 95% specificitou, který použijeme pro nemoc s prevalencí 1 %, vykáže 16% prediktivní hodnotu pozitivního testu (tedy pouze 16 % lidí s pozitivním testem má skutečně uvažovanou nemoc), zatímco prediktivní hodnota negativního testu je 99,9 %. Komplexní hodnocení doplňují hodnoty věrohodnostního poměru testů s různou senzitivitou a specificitou. Vysoce specifický test nebude pravděpodobně produkovat falešně pozitivní výsledky, jeho pozitivní výstup je věrohodný jako pravdivá pozitivita. Naopak vysoce senzitivní test má sníženou pravděpodobnost falešně negativních výsledků a jeho negativní výsledek je věrohodný.

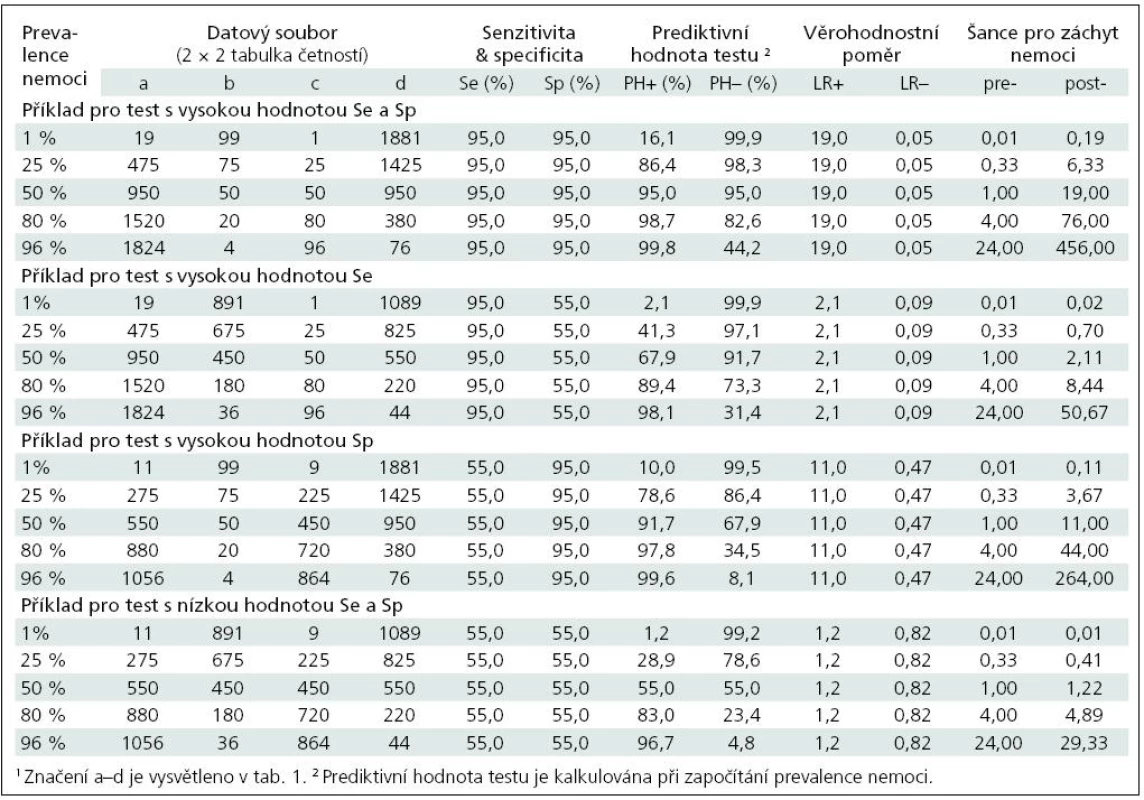
Tímto dílem seriálu končíme výklad o hodnocení diagnostických testů vedoucích k binárnímu výsledku (pozitivní, negativní). Doufáme, že jsme čtenářům vysvětlili význam různých ukazatelů kvality testů a seznámili jsme je s jejich výpočty, včetně intervalů spolehlivosti. Závěrem znovu zdůrazněme, že o praktickém nasazení žádného, byť sebelepšího, testu nelze rozhodovat pouze z jeho senzitivity a specificity. V úvahu musíme vždy brát účel nasazení daného testu (např. zda je pro zadaný úkol lepší vysoká senzitivita nebo specificita) a především prevalenci daného onemocnění v populaci. Jen tak lze optimalizovat věrohodnost a prediktivní sílu dosažitelných výstupů.

Na konec se pokusíme danou problematiku zobecnit. Popsaná metodika hodnocení není využitelná pouze pro validaci diagnostických testů, tedy pro situace, kdy proti sobě stojí výstup testu (T+/T–) a přítomnost/nepřítomnost nemoci (N+/N–). Některé ukazatele lze využít i pro hodnocení rizikových nebo prognostických faktorů pro vznik a vývoj nemoci. Rizikový faktor (znak) stojí v takovém případě na pozici diagnostického testu a nabývá opět dvou hodnot (přítomen/nepřítomen; +/–). V analýze potom například sledujeme, jak přítomnost faktoru souvisí s výskytem nemoci nebo s negativním vývojem nemoci. Ačkoli je samozřejmě interpretace jiná než u klasického diagnostického testu, datová základna je stejná (2 × 2 tabulka četností) a její analýza může využívat ukazatele, jako jsou specificita, senzitivita, prediktivní hodnota i věrohodnostní poměr. V podstatě zde analyzujeme informační (důkazní) hodnotu znalosti o přítomnosti nějakého znaku (např. v anamnéze pacienta). Číselnou ukázku takového hodnocení nabízí příklad 3.

Úlohu hodnotící význam rizikových (prognostických) faktorů lze zobecnit ještě dále. V podstatě každý výsledek testu nebo zjištění přítomnosti rizikového faktoru můžeme považovat za jistý důkaz směřující k prokázání nějaké skutečnosti. U diagnostických testů jde o prokázání přítomnosti nemoci. Logicky očekáváme, že se znalostí výsledku testu naše schopnost prokázat přítomnost nebo nepřítomnost choroby poroste a poroste také jistota a věrohodnost našich závěrů. Tímto jsme popsali obecný model práce s důkazy nejen v medicíně, ale např. i v soudnictví anebo v ekonometrii. Před zjišťováním důkazů máme pre-testovou šanci záchytu daného jevu. Při znalosti důkazů (výstupů testů), které mají určitý věrohodnostní poměr, očekáváme, že tato šance poroste. Obecně tedy platí již zmíněný vztah post-testová šance = pre-testová šance * věrohodnostní poměr. S využitím obecnější terminologie potom platí aposteriorní šance = apriorní šance * věrohodnostní poměr.

Věrohodnostní poměr (LR) tudíž obecně vyjadřuje „sílu“ důkazu. Důkazem nemusí nutně být diagnostický test. Ve stejné pozici může stát jakýkoli údaj, který dáváme do souvislosti s posuzovaným cílovým stavem (přítomnost nemoci, kritický vývoj nemoci, propad hodnoty bodu na burze, zločin spáchaný danou osobou). Vztah pro výpočet LR používaný u diagnostických testů (tab. 1) můžeme obecně přepsat do vztahu:

LR = P(sledovaný jev nastane | hypotéza platí) / P(sledovaný jev nastane | hypotéza neplatí),

kde sledujeme podíl dvou podmíněných pravděpodobností, nastání jevu při platnosti hypotézy k nastání téhož jevu při neplatnosti hypotézy. LR > 1 znamená, že daný jev svědčí spíše pro platnost hypotézy, LR < 1 naopak znamená, že daný jev je asociován spíše s neplatností hypotézy. Podle hodnoty LR můžeme potom jevy (důkazy, faktory, výsledky testů) posuzovat a srovnávat. Například hodnoty LR 2, 10 a 1 000 označují tři faktory, jejichž přítomnost je s rostoucí věrohodností asociována s platností nějaké hypotézy nebo s přítomností nějaké sledované vlastnosti. Hodnota LR obecně určuje kontext dokazování, samozřejmě společně s prevalencí hledaného nebo zkoumaného jevu (výskyt choroby u pacienta, zločin spáchaný danou osobou...).

doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz