-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Analýza dat v neurologii
VIII. Binomické rozdělení
Autoři: L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů: Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2008; 71/104(2): 229-232
Kategorie: Okénko statistika
Tento díl statistického seriálu věnujeme pragmatickému vysvětlení binomického rozdělení, které je využíváno pro modelování diskrétních znaků. Jen pro připomenutí uveďme, že rozdělení pravděpodobnosti vzniká tím, že jsme schopni výsledky opakovaného náhodného experimentu uspořádat na číselné ose a elementárním jevům přiřadíme pravděpodobnost jejich výskytu. Z předchozích dílů by mohl vzniknout nesprávný dojem, že rozdělení pravděpodobnosti se používají převážně pro spojité náhodné veličiny, tedy takové, které mohou nabývat všech reálných hodnot. Avšak naprosto stejný význam mají modelová rozdělení pravděpodobnosti pro diskrétní náhodné veličiny. Pouze formální vyjádření jejich distribuční funkce je odlišné, neboť tyto znaky mohou nabývat pouze diskrétních (od sebe oddělených) hodnot. Jejich distribuční funkce je tedy typicky schodovitá.
Význam pravděpodobnostních rozdělení je u diskrétních znaků stejný jako u znaků spojitých. Známe-li rozdělení, a tím i distribuční funkci, známe tak pravděpodobnost, s jakou může znak nabývat konkrétních hodnot. S využitím příslušného rozdělení můžeme tuto pravděpodobnost dokonce predikovat nebo můžeme simulovat různé situace. Popisem binomického rozdělení neprovádíme žádný virtuální výlet do světa matematiky, toto rozdělení reálně existuje kolem nás a není problém pro něj najít ilustrativní příklady „ze života“.
Začněme poměrně strohou definicí. Binomické rozdělení popisuje četnost výskytu náhodného jevu v n nezávislých pokusech, v nichž má tento jev stále stejnou pravděpodobnost, že nastane. Smysl binomického rozdělení není těžké pochopit. Již jsme probrali, že u rozdělení normálního je hodnocena pravděpodobnost různých hodnot, např. výšky postavy. Výška postavy v cm je tedy na ose X. Binomické rozdělení podobně sleduje výskyt nějakého jevu a na ose X, bude tedy vyneseno tolikrát, kolikrát tento jev v opakovaných pokusech nastal. Učebnicovým příkladem je hod mincí, kde sledujeme, zda a kolikrát padne líc. Hodíme-li celkem 5krát (n = 5), pak líc nemusí nutně padnout ani jednou a nejvíce může padnout právě pětkrát. Na ose X budou tedy diskrétní hodnoty 0, 1, 2, 3, 4, 5 a pravděpodobnost, že nastane konkrétní hodnota můžeme zjistit pomocí binomického rozdělení, pokud jsou splněny jeho předpoklady. Jednotlivé hody mincí musí být vzájemně zcela nezávislé a pravděpodobnost nastání sledovaného jevu se v opakovaných pokusech nesmí měnit. U běžné mince v běžných podmínkách je tato pravděpodobnost 0,5 a obecně ji označujeme p, při popisu cílové populace jako π. Hodnota p je parametrem binomického rozdělení a určuje pravděpodobnost nastání jevu v jednotlivých experimentech. Tyto musí být nastaveny tak, aby byla možná již jen jedna další možnost, tedy jev opačný nastávající s pravděpodobností 1 – p (někdy je označováno jako 1 – p = q).
Střední hodnota znaku s binomickým rozdělením je E(X) = n × p, rozptyl je D(X) = n × p × (1 – p). Jelikož p může nabývat hodnot pouze od 0 do 1, snadno zjistíme, že D(X) je největší při p = 0,5. Paralelou E(X) u normálního rozdělení by byl aritmetický průměr jako střed rozdělení a paralelou D(X) rozptyl hodnot.
S pravděpodobností p nastání jevu někdy v běžných interpretacích ne zcela správně pracujeme. Hodíme-li mincí 10krát, potom střední hodnota binomického rozdělení jednoduše udává nejpravděpodobnější četnost sledovaného jevu (líc), což je při p = 0,5 celkem n × p = 5. Ale pozor, to rozhodně neznamená, že nemůže padnou líc mince i 10krát a naopak třeba ani jednou. Každá hodnota znaku X může nastat, i když s jinou pravděpodobností. I kdyby měl sledovaný jev pravděpodobnost nastání v jednotlivém experimentu například 0,95, je s určitou, byť velmi malou, pravděpodobností možné, že se v 10krát opakovaném experimentu neobjeví ani jednou. Konkrétně tato pravděpodobnost je při n = 10 a p = 0,95 rovna P(X = 0) = 9,8 × 10–14.
A naopak relativně málo pravděpodobný jev může nastat i opakovaně za sebou. Abychom tyto pravděpodobnosti byli schopni spočítat, musíme použít vztah uvedený na obr. 1. Doufejme, že poněkud složitější vzorec čtenáře neodradí, jeho výpočet je jednoduchý a vyžaduje pouze aplikaci faktoriálů hodnot zahrnutých v kombinačním čísle. Výpočet je rozepsán pro příklad 5krát opakovaného experimentu v tab. 1. Obr. 1 dále dokládá tyto skutečnosti:
- binomický znak X vyjadřuje četnost sledovaného jevu v n opakováních a nabývá hodnot od 0 do n
- čím vícekrát opakujeme experiment, tím menší relativní podíl připadá na jednotlivé hodnoty X, neboť všechny dohromady musí nastat s pravděpodobností 1, nebo kumulativně 100 %
- rozdělení s p = 0,5 je symetrické kolem středu osy X, menší nebo větší p posouvá střed rozdělení směrem k limitním hodnotám, tedy směrem k hodnotě 0 nebo N
- hodnota p = 0,1 neznamená automaticky 10% výskyt daného jevu, všechny hodnoty od 0 do n mohou nastat, i když s různou pravděpodobností.
Obr. 1. Binomické rozložení jako model. 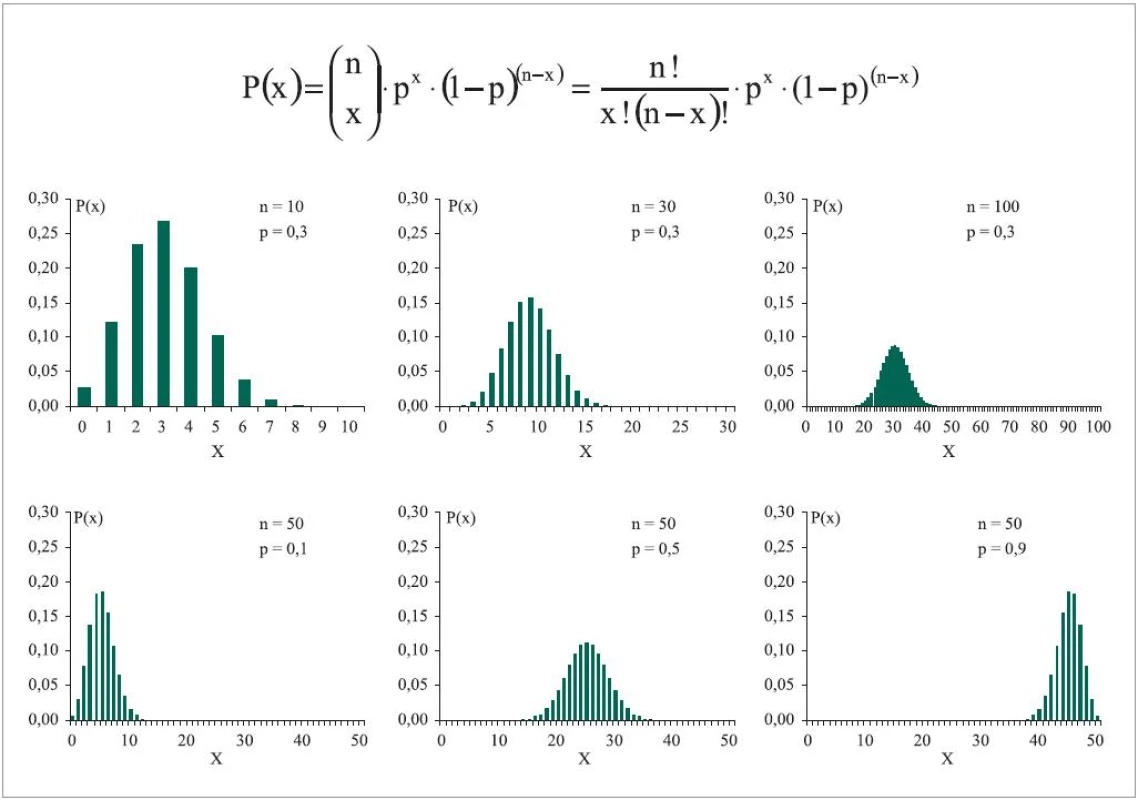
Tab. 1. Pravděpodobnost četnosti jevu dle binomického rozdělení. 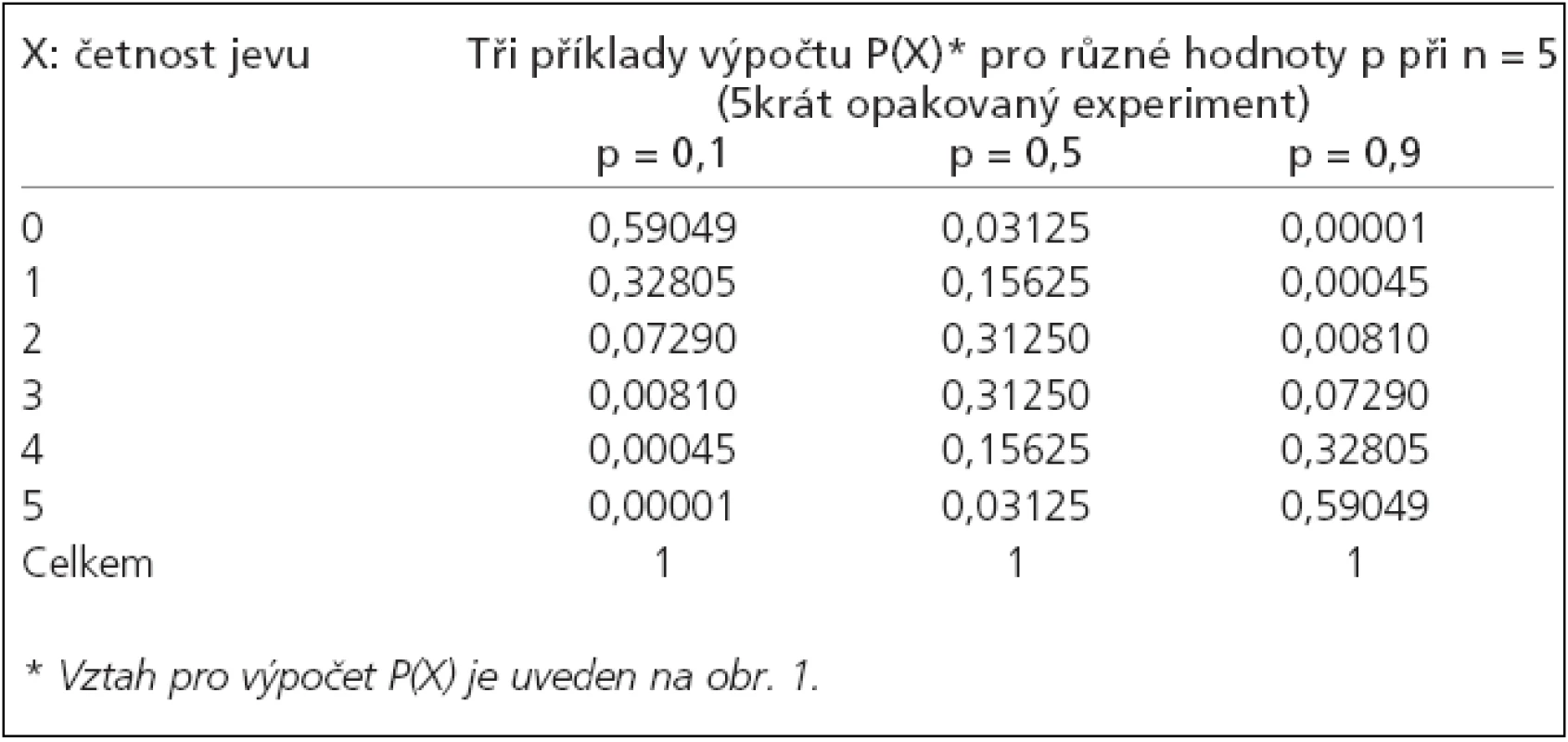
Příklad na obr. 1 usnadní i pochopení dvou extrémních případů. První je v praxi klinického výzkumu málo využitelný a jde o situaci, kdy experiment opakujeme pouze jednou. Pokud je speciálně n = 1, jde o tzv. alternativní rozdělení a daný jev buď nenastane, nebo nastane jednou. Druhým extrémem je, že náhodný experiment opakujeme mnohokrát. Tedy máme velmi velký počet jedinců, objektů nebo situací, u kterých hodnotíme (vždy u jednoho po druhém), zda jev nastal nebo ne. Na obr. 1 vidíme, že rozložení za této situace začne vytvářet téměř spojitý obrázek. V takovém případě práce s výsledky vyžaduje aproximaci na vhodný typ spojitého rozdělení, např. při p = 0,5 aproximaci na normální rozdělení. Při n = 1 000 jistě nemá smysl ptát se na pravděpodobnost, že se jev objeví přesně například u 897 jedinců. Osa X bude přirozeně tříděna do intervalů a interpretace i grafické vyjádření bude připomínat práci s rozdělením hodnot spojité veličiny.
Binomické rozdělení je užitečným nástrojem, popisujícím velké množství reálných situací. Známe-li hodnotu p a n, můžeme rovnici na obr. 1 pohodlně používat k velmi cenným výpočtům. Jako příklad uveďme tyto:
- výpočet pravděpodobnosti nastání libovolného počtu jevů, od 0 až do maxima n
- simulační výpočet, jak se změní pravděpodobnost při snížení nebo zvýšení n
- simulační výpočet, jak se mění tvar rozdělení při změně p.
V experimentální praxi je p často neznámé a sledování provádíme právě proto, abychom ho odhadli. I v případě binomického rozdělení odhadujeme hodnotu v cílové populaci π, a to jednak bodovým odhadem, anebo pomocí intervalu spolehlivosti. Příklad výpočtu 95% intervalu spolehlivosti uvádí obr. 2. Interval má stejnou interpretaci jako např. u odhadu aritmetického průměru normálního rozdělení. Udává pravděpodobnostní hranice výskytu opakovaně odhadovaných hodnot π. Pokud bychom odhad opakovali 100krát při stejném n, pak by se získané odhady p1, p2 až p100 celkem 5krát mohly dostat mimo hranice 95% intervalu spolehlivosti. Interval spolehlivosti informuje čtenáře o stupni nejistoty při odhadu pravděpodobnosti nastání jevu. Pro další výpočty pak můžeme podle okolností použít i hranice intervalu místo vlastní hodnoty p. Například při odhadu pravděpodobnosti škodlivého jevu lze při analýze rizik pracovat s horní hranicí intervalu spolehlivosti jako s bezpečnějším údajem. Snižujeme tak pravděpodobnost podhodnocení rizika.
Obr. 2. Výpočet intervalu spolehlivosti pro parametr π binomického rozložení. 
Z výpočtu na obr. 2 vidíme všechny obecně platné vlastnosti intervalů spolehlivosti, z těch hlavních uveďme následující:
- je použit 97,5% kvantil standardizovaného normálního rozložení (Z), počítáme tedy oboustranný 95% interval. Pokud bychom použili kvantil s nižší pravděpodobnostní hodnotou, byl by číselně menší než Z0,975 = 1,96 (např. Z0,95 = 1,645 by vedl k 90% intervalu) a interval by se numericky zužoval. A naopak dosazením Z0,995 = 2,576 bychom hranice rozšířili a získali bychom 99% interval
- šířka intervalu závisí na hodnotě p, přičemž nejširší bude pro p = 0,5
- šířka intervalu logicky závisí na hodnotě n, čím větší n, tím přesnější je odhad π, a tím je interval užší.
Výpočet intervalu spolehlivosti na obr. 2 je založen na předpokladu, že odhad p se chová podle modelu normálního rozložení. Proto je ve vztahu používán kvantil standardizovaného normálního rozložení,
a proto je interval symetrický. Avšak tento předpoklad samozřejmě nebude platit u velmi nízkých a vysokých hodnot p, neboť ty jsou ohraničeny hodnotou 0 nebo 1. Například, naměříme-li při malém n = 10 hodnotu p = 0,2 nebo nižší, budeme mít problémy se spodní hranicí intervalu spolehlivosti. Z tohoto důvodu uvádíme na obr. 3 a 4 vztahy pro asymetrický interval spolehlivosti, kde je používáno tzv. Fisher-Snedecorovo rozdělení. Toto rozdělení má kvantily mezinárodně označované jako F a má dva druhy stupňů volnosti, které jsou označovány jako ν1 a ν2. Hodnoty kvantilů F pro danou dvojici hodnot ν1 a ν2 lze nalézt v tabulkách, statistickém software nebo i v MS Excel. Výpočet na obr. 3 a 4 umožní ošetřit intervalem spolehlivosti odhady parametru π blízké limitním hodnotám 0 nebo 1.Obr. 3. Výpočet intervalu spolehlivosti pro parametr binomického rozdělení bez aproximace na normální rozdělení – vztahy. 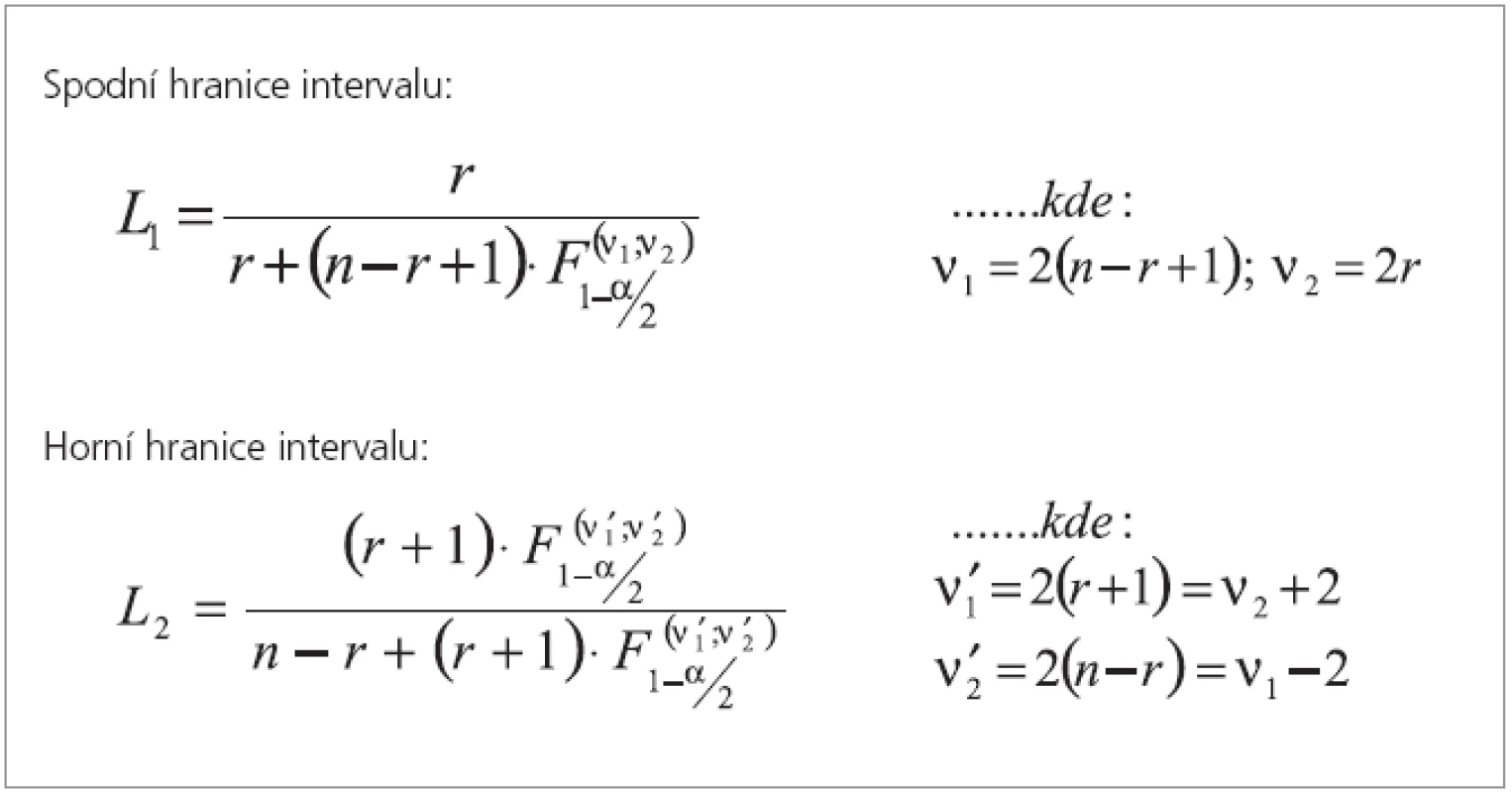
Obr. 4. Výpočet intervalu spolehlivosti pro parametr binomického rozdělení bez aproximace na normální rozdělení – příklad. 
Další možností, jak pracovat s binomickým rozdělením při velmi nízkých hodnotách p, je aproximace na tzv. Poissonovo rozdělení. Tato aproximace je efektivní při n > 30 a p < 0,1. Poissonovo rozdělení umožňuje modelování výskytu vzácných a velmi vzácných jevů. Tomuto tématu bude věnován další díl našeho seriálu.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Štítky
Dětská neurologie Neurochirurgie Neurologie
Článek Roztroušená sklerózaČlánek Žena a iktusČlánek Soutěž o nejlepší publikaceČlánek Webové okénko
Článek vyšel v časopiseČeská a slovenská neurologie a neurochirurgie
Nejčtenější tento týden
2008 Číslo 2- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Moje zkušenosti s Magnosolvem podávaným pacientům jako profylaxe migrény a u pacientů s diagnostikovanou spazmofilní tetanií i při normomagnezémii - MUDr. Dana Pecharová, neurolog
- Magnosolv a jeho využití v neurologii
- Nejčastější nežádoucí účinky venlafaxinu během terapie odeznívají
-
Všechny články tohoto čísla
- Roztroušená skleróza
- Zlyhanie farmakologickej antiepileptickej liečby
- Patofyziologie bloku vedení u neuromuskulárních chorob
- Žena a iktus
- Soutěž o nejlepší publikace
- Diagnostika hyponatremií v neurointenzivní péči: úloha renálních funkčních parametrů
- Úskalí diagnostiky a léčby flekčně-distrakčních poranění hrudní a bederní páteře: prospektivní studie
- Efekt endoskopické a klasické operace pro syndrom karpálního tunelu
- Mírná řízená hypotermie jako neuroprotektivní metoda při pozdních ischemických komplikacích v resuscitační péči u pacientů s těžkým spontánním subarachnoidálním krvácením při ruptuře aneuryzmatu
- Komentář ke článku Charvát F, Mašková J, Lacman J, Beneš V. Intrakraniální angioplastika a implantace stentu u aterosklerotických lézí.
- Intrakraniální angioplastika a implantace stentu u aterosklerotických lézí
- Familiárna agregácia Parkinsonovej choroby: genealogická štúdia
- PCR diagnostika herpetických virů u pacientů s akutní „idiopatickou“ parézou lícního nervu
- Výsledky léčby gliomů nízkého stupně malignity u dětí (retrospektivní analýza dat)
- Komentář k článku Valchář J et al. Hemangioblastom a jeho léčba pomocí Leksellova gama nože
- Hemangioblastom a jeho léčba pomocí Leksellova gama nože
- Syndrom Smithové-Magenisové: kazuistika
- Webové okénko
-
Analýza dat v neurologii
VIII. Binomické rozdělení -
Zpráva z Prvního kongresu Mezinárodní společnosti intraoperační neurofyziologie
Luzern, Švýcarsko 15.–18. 11. 2007 - Závěry „Winter GLIO TRACK Meeting“ 2008
- Zpráva z Neurovaskulárního kongresu, Ostrava 2008
- K životu a práci prof. MUDr. P. Varsika, DrSc. (18. 9. 1941–29. 12. 2005)
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Roztroušená skleróza
- Hemangioblastom a jeho léčba pomocí Leksellova gama nože
- Syndrom Smithové-Magenisové: kazuistika
- Výsledky léčby gliomů nízkého stupně malignity u dětí (retrospektivní analýza dat)
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



