Analýza dat v neurologii III.
Nebojme se mediánu a robustních statistik

Předchozí kapitoly tohoto statistického „minitutoriálu“ otevřely otázku volby statistik středové tendence, neboli ukazatelů střední hodnoty souboru měření. A ve vazbě na ně také ukazatelů variability daného souboru měření. Otázka jednoduchá, zároveň ale velmi závažná, protože nesprávnou volbou můžeme hned na počátku analýzy velmi snížit šanci na kvalitní výsledek. V této kapitole se chceme k tomuto problému pragmaticky vrátit a popsat pravidla výběru těchto ukazatelů. Při ještě únosné míře zjednodušení nám bude stačit několik málo následujících odstavců a pokryjeme naprostou většinu praktických situací. Na této jednoduché problematice lze také dobře doložit pozici analýzy dat jako pouhého nástroje, který nesmí být používán dogmaticky podle zkostnatělých návodů neumožňujících samostatné uvažování. I v kvalitních odborných časopisech se totiž dnes můžeme setkat s viditelně nesprávně použitými statistikami, které byly aplikovány podle zlatého pravidla „udělám to jako všichni ostatní, ať nejsou problémy s oponenturou“. A tak datům dominuje výpočet aritmetického průměru, někdy počítaný i na ordinálních stupnicích anebo asymetricky rozložených datech. Ale o tom bude následující text.

Na počátku ovšem vždy stojí soubor dat, pro příklad nyní uvažujme hodnoty spojité, například koncentrace látek A-C, jak je ukazuje tab. 1. Chceme-li tyto hodnoty prezentovat sumárními statistikami středu, pak v učebnicovém zjednodušení vybíráme z následujících možností: modus, medián a aritmetický průměr:

• Modus je nejčastější hodnota v souboru, využitelný pouze s touto interpretací; rozhodně není úplně ideální pro malé soubory spojitých čísel, jak je vidno i z tab. 1. Síla této statistiky vyniká především při sumarizaci velkých souborů nominálních a ordinálních dat.
• Medián je frekvenční střed a platí, že polovina hodnot souboru je menších než medián a polovina větších. Medián tedy nabízí sympatickou interpretaci: jde o ukazatel typické hodnoty souboru.
• Aritmetický průměr je kvantitativní charakteristika, která je těžištěm číselné osy – ukazuje průměrnou hodnotu (velikost) znaku na jedno měření v souboru (jedinec, měřený objekt ....).

Prvním pragmatickým krokem při výběru statistiky středu je prohlídka frekvenčního rozložení hodnot a kontrola jeho tvaru, případně identifikace odlehlých hodnot. Tuto tzv. analýzu frekvenčních tabulek jsme probírali v minulé kapitole. Prohlídka může probíhat i graficky a pokud si výběrové rozložení zidealizujeme jakoby bylo naměřeno na velkém až nekonečném souboru, získáme 3 základní modelové tvary, které ukazuje obr. 1. Statistiky středu potom volíme podle potřeb a podle tvaru daného rozložení.

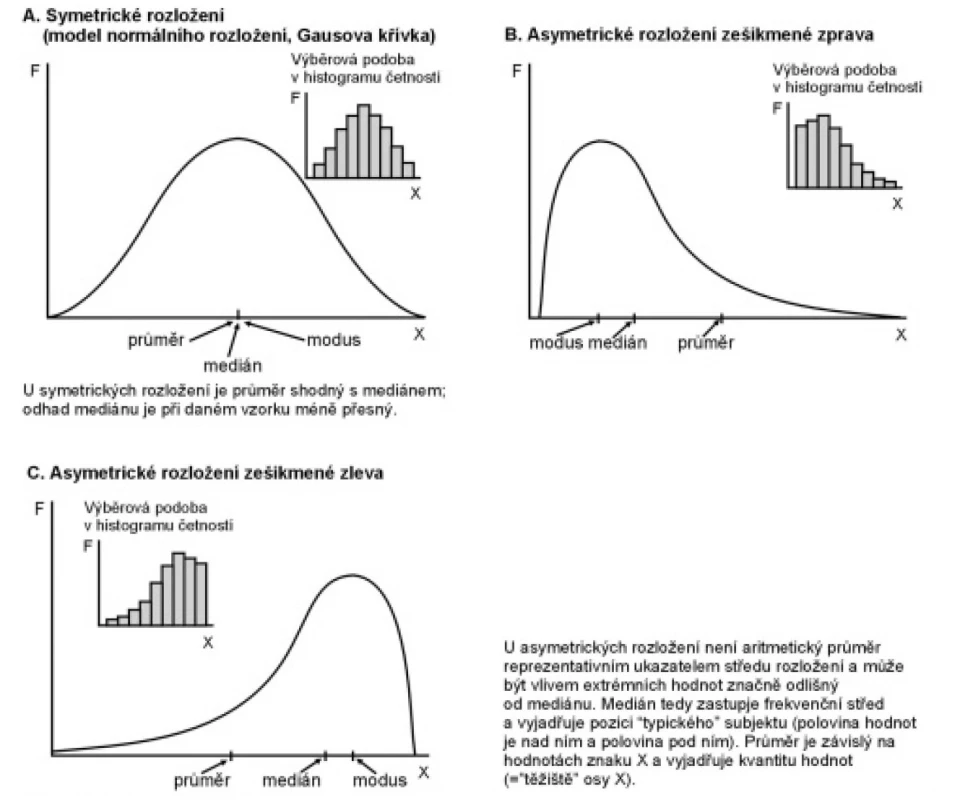
Všimněme si, že u spojitých dat lze všechny 3 nabídnuté statistiky středu spočítat současně. Zvláště v dnešní době PC je to otázka několika sekund. Modus, medián i průměr také „číselně“ leží na téže číselné ose (na obr. 1 označena jako X) a mají jednotky této osy. S vlastním výpočtem tedy problémy nebývají, daleko složitější je vybrat metriku se správnou interpretací. Zde je několik pragmatických pravidel:

• Modus a medián se interpretačně liší od průměru, neboť jejich význam zasahuje nejen čísla na ose X, ale také frekvenční údaje na ose Y – tedy „kolikrát co bylo naměřeno“ a „kde jaká hodnota leží ve vztahu k dalším“. Medián při svém výpočtu přímo vyžaduje seřadit hodnoty podle velikosti a následně je vybrán frekvenční střed.
• Naopak průměr je kvantitativní míra a jeho výpočet žádné řazení hodnot podle velikosti nevyžaduje. Průměr se v podstatě frekvenčního výskytu hodnot netýká a z hlediska tvaru rozložení je doslova „slepý“.
• Objeví-li se mezi naměřenými hodnotami odlehlé číslo, nebo číslo chybné až řádově odlišné, pak jeho přítomnost změní hodnotu mediánu jen minimálně (zvláště u větších souborů se na mediánu neprojeví vůbec). Avšak aritmetický průměr jako „frekvenčně slepá“ kvantitativní metrika může zareagovat i velkým posunem. A je-li toto nové měření zcela chybné, pak i průměr přestává být reprezentativním ukazatelem středu hodnot. Jako příklad uveďme soubor C v tab. 1, v němž k naměřeným hodnotám v souboru B přibylo odlehlé číslo 720 a zcela změnilo hodnotu průměru bez viditelného vlivu na medián. Proto medián a podobné pořadové ukazatele označujeme za robustní statistiky, neboť nejsou citlivé na tyto extrémní situace.
• Medián, průměr i modus lze vzájemně srovnávat, neboť leží na téže číselné ose a u daného souboru hodnot mají stejné jednotky. Velký rozdíl v hodnotě mediánu a průměru je indikátorem asymetrie rozložení dat nebo přítomnosti odlehlých hodnot.
• U asymetrických rozložení nebo při podezření na odlehlé hodnoty je medián vždy reprezentativnějším ukazatelem středu rozložení než průměr

Pokud máte z výše uvedeného dojem, že medián je „chytřejší“ statistika než průměr, je to jistě pravda. Stíhá totiž sledovat nejen kvantitu hodnot, ale i tvar rozložení. Nadto je to statistika univerzálnější, neboť vyžaduje pouze srovnání hodnot podle velikosti, což splňují i ordinální znaky a nejrůznější skóre. Pro ně je medián jednoznačnou volbou, a naopak aritmetický průměr zde není definován a neměl by se používat. Zcela jednoduše řečeno, nechcete-li mít žádné starosti s rozložením hodnot, pak používejte medián jako robustní a univerzální statistiku středu. Vyžadují-li okolnosti výpočet aritmetického průměru, pozorně kontrolujte symetrii rozložení a hlavně případné odlehlé hodnoty.

Ostatně tvar rozložení se vyplatí prohlédnout vždy, ať již frekvenční tabulkou, nebo histogramem, které mohou odhalit řadu vážných skutečností. Typickým příkladem může být tzv. bimodální rozložení hodnot dokumentované na obr. 2. Zde díky symetrii rozložení nabývá medián i průměr stejných hodnot, ale již sám obrázek indikuje neobvyklý tvar s následujícími možnými interpretacemi:

• Znak X přispívá k rozlišení dvou subpopulací subjektů a měli bychom dále zkoumat jaké subjekty patří do vyšších, a naopak do nižších hodnot. Bimodalita rozložení je typická pro diagnosticky hodnotné znaky odlišující zdravé jedince od nemocných, nebo různá stadia choroby apod.
• Bimodální tvar může ale také indikovat vážné problémy ve sběru dat, když nebyl z nějakého důvodu adekvátně zachycen střed rozložení. Tato situace může nastat především u menších vzorků, u nichž bimodalitu v rozložení potlačí následné zvětšení souboru.

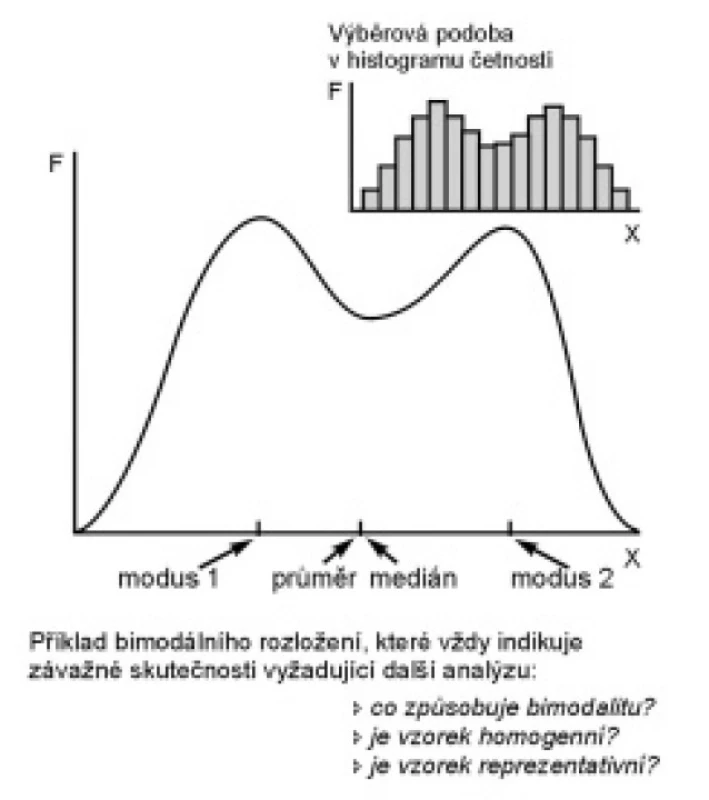
Jistě jste zaznamenali, že ve výše uvedeném textu zazněl jasný zákaz pouze pro výpočet aritmetického průměru u ordinálních dat. U spojitých dat lze spočítat průměr i medián pro jakékoli tvary rozložení, s i bez odlehlých hodnot. To ostatně ukazuje i příklad v tab. 1. Znamená to tudíž, že průměr i medián existují i u těchto problematických rozložení, každá statistika ale říká něco zcela jiného. Budeme-li například měřit obsah nějakého prvku v mg na litr v heterogenní matrici, můžeme dostat následující sadu měření: 0, 0, 0, 5, 0, 0, 0, 400. Medián, a tedy typická sonda je 0 mg/l, ale průměrná sonda (tedy něco jako výtěžnost) je 50,6 mg/l. Medián i průměr lze použít současně, a při správné interpretaci tak získáme více informací. Na rozdíl od ordinálních a nominálních dat nejsou tedy striktní zákazy u spojitých dat na místě.

U dat ordinálních se naopak aritmetickému průměru vyhýbejme, jakkoli život vyžaduje jednoduchá řešení a medián stále zní mnoha lidem jako cizí slovo. Příkladem může být známkování ve škole, je-li vyjadřováno číselně škálou 1 až 5. Mějme studenta A se známkami 2, 2, 2, 2, 1 a vedle něj studenta B se známkami 1, 1, 1, 1, 5. Oba mají aritmetický průměr 1,8, a přitom student A je typický „dvojkař“ (medián = 2) a student B je typický jedničkář, který měl zřejmě jednu slabou chvilku a dostal známku 5. Použít zde aritmetický průměr a hlavně pouze aritmetický průměr není správné, ani spravedlivé. Při přednáškách tyto příklady vyvolají vždy poměrně bouřlivé diskuse se studenty, a vyučující pak musí medián obhajovat:

• Známkování na škále 1 až 5 tvoří ordinální stupnici. Jejím středem je definičně medián, nikoli průměr. Víme pouze že 2 je horší než 1, nevíme ale „o kolik“ horší. Stupnice není kvantitativní.
• V běžném systému není definována rovnoměrná vzdálenost mezi 1 a 2, 2 a 3 anebo 4 a 5. Naopak lze předpokládat, že tyto vzdálenosti jsou rozdílné u lepších a horších známek, a liší se i podle předmětu, formy zkoušení, učitele anebo školy. Kvantitativní sumarizace průměrem pak nutně vede ke srovnávání nesrovnatelného.

Samozřejmě i pro příklad školních známek a ordinálních dat existuje jisté výjimečné řešení, které spočívá v kvantitativním vyjádření vzdálenosti mezi jednotkami stupnice. Například bodováním od 0 do 100 % a následně rovnoměrným dělením do škály 1-5, pak je ale možné přímo kalkulovat průměr na získaných bodech. Výše uvedený komentář se samozřejmě v plné míře vztahuje i na nejrůznější skóre a ordinální stupnice používané v neurologii a v medicíně obecně. I zde je medián jasnou volbou, zvláště je-li stupnice tvořena jen několika málo body.

Čtenář, který od této kapitoly čekal vojensky jasná doporučení, je jistě zklamán. Výběr statistik středu sice svá pravidla má (ordinální stupnice a medián, symetrická vs. asymetrická rozložení, odlehlé hodnoty, apod), nicméně nejde o pravidla striktní a konečný výstup vyžaduje cit a odborný vstup analytika. To ale vnímejme spíše pozitivně než negativně. A jak už to tak bývá i v jiných situacích, lze si vybrat mezi jednoduchým a univerzálním řešením, anebo zvolit řešení informačně obsažnější a specifičtější, ovšem při splnění jistých vstupních podmínek. Hlavně pozor na zneužití, ať již vědomé nebo nevědomé. Jistě si budete po přečtení tohoto článku dávat větší pozor například na údaje o průměrném platu českého občana. Nespokojíte se s pozitivně vypadající hodnotou x tisíc Kč, budete jistě uvažovat o tvaru rozložení hodnot, o vlivu možných odlehlých hodnot a jistě se zeptáte i na mediánový, tedy „typický“ plat. A najednou může celá interpretace vypadat úplně jinak. V tom je složitost, ale i krása analýzy dat.

doc. RNDr. Ladislav Dušek, Dr.

Institut biostatistiky a analýz, Masarykova univerzita, Brno

e-mail: dusek@cba.muni.cz