-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaEffect of Correlated tRNA Abundances on Translation Errors and Evolution of Codon Usage Bias
Despite the fact that tRNA abundances are thought to play a major role in determining translation error rates, their distribution across the genetic code and the resulting implications have received little attention. In general, studies of codon usage bias (CUB) assume that codons with higher tRNA abundance have lower missense error rates. Using a model of protein translation based on tRNA competition and intra-ribosomal kinetics, we show that this assumption can be violated when tRNA abundances are positively correlated across the genetic code. Examining the distribution of tRNA abundances across 73 bacterial genomes from 20 different genera, we find a consistent positive correlation between tRNA abundances across the genetic code. This work challenges one of the fundamental assumptions made in over 30 years of research on CUB that codons with higher tRNA abundances have lower missense error rates and that missense errors are the primary selective force responsible for CUB.
Published in the journal: . PLoS Genet 6(9): e32767. doi:10.1371/journal.pgen.1001128
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1001128Summary
Despite the fact that tRNA abundances are thought to play a major role in determining translation error rates, their distribution across the genetic code and the resulting implications have received little attention. In general, studies of codon usage bias (CUB) assume that codons with higher tRNA abundance have lower missense error rates. Using a model of protein translation based on tRNA competition and intra-ribosomal kinetics, we show that this assumption can be violated when tRNA abundances are positively correlated across the genetic code. Examining the distribution of tRNA abundances across 73 bacterial genomes from 20 different genera, we find a consistent positive correlation between tRNA abundances across the genetic code. This work challenges one of the fundamental assumptions made in over 30 years of research on CUB that codons with higher tRNA abundances have lower missense error rates and that missense errors are the primary selective force responsible for CUB.
Introduction
Protein production is the most energetically expensive metabolic process within a cell [1]–[4]. However, like all biological processes, protein translation is prone to errors. The biological importance of these translation errors and their impact on coding sequence evolution, especially the evolution of codon usage bias (CUB), depends on both their effects on protein function and their frequencies. Translation errors fall into two categories: nonsense errors and missense errors. Nonsense errors, also referred to as processivity errors, occur when a ribosome prematurely terminates translating a coding sequence. Missense errors occur when the wrong amino acid is incorporated into a growing peptide chain. Although many possible factors such as mRNA stability and recombination likely contribute to the evolution of CUB, selection against translation errors and biased mutation are thought to be the primary forces [5]–[11].
Most researchers believe that CUB results primarily from selection against missense errors or, equivalently, for translational accuracy (see [10], [12]–[15]). In addition to limited empirical observations, the main evidence cited as supporting this belief includes the fact that preferred synonymous codons (i.e. the codons over-represented in high expression genes) have higher cognate tRNA abundances and that these codons are also favored at evolutionarily conserved sites [12], [13]. While the preferred codons may indeed be ‘optimal’ in some limited sense, as we demonstrate below, the idea that they minimize missense error rates is based on an overly simplistic understanding of the relationship between tRNA abundances and missense error rates.
The effect of missense errors on protein function is equivalent to a non-synonymous point mutation. Because amino acids with similar properties are clustered within the genetic code [16]–[19], the genetic code is generally considered to be adapted to minimize the phenotypic effects of point mutations and missense errors. However, despite its importance, the adaptedness of tRNA abundances across the genetic code to reduce the rate of translation errors has received almost no attention. For instance, in E. coli the average nonsense and missense error rates are estimated to be on the order of to per codon, respectively [10], [20]–[25]. This implies that for an average length gene of amino acids, about 3–26% of its protein products will contain at least one translation error. However, since the only available estimates of missense error rates are for specific amino acid misincorporations [20]–[22], these rates are likely gross underestimates as they do not take into account all possible amino acid misincorporations at that codon.
Currently, missense errors are thought to be the result of competition between tRNAs with the right amino acid (cognates) and the ones with the wrong amino acids (near-cognates) for the codon at the ribosomal A-site [25]–[27]. A near-cognate tRNA is characterized by a single codon-anticodon nucleotide mismatch and codes for an amino acid different from that of the A-site codon [28]–[30]. As a result of this competition, the rate of missense errors at a codon should be strongly affected by the abundances of both cognate and near-cognate tRNAs [25]. For example, an increase in cognate tRNA abundances is predicted to lead to a decrease in a codon's missense error rate. In contrast, an increase in near-cognate tRNA abundances is predicted to lead to an increase in a codon's missense error rate [25].
Previous studies of CUB have generally assumed that amongst a set of synonymous codons, the one with the correspondingly highest tRNA abundance is the one with the lowest missense error rate. However, because missense error rates are thought to be a function of both cognate and near-cognate tRNA abundances, if tRNA abundances are positively correlated across the genetic code this assumption may not hold. In this study we ask a fundamental question, “Are tRNA abundances correlated across the genetic code?” Finding that tRNA abundances are indeed generally positively correlated across a wide range of prokaryotes, we then ask, “How does the distribution of tRNA abundances affect the relationship between codon translation and error rates?” This question is of critical importance because the currently favored explanation of CUB, what we will refer to as the standard model, implicitly assumes that codons with the highest translation rates are also the ones with the lowest missense error rates. Our results indicate that this basic assumption only holds for a limited subset of amino acids. As a result, our work strongly suggests that missense errors play a smaller role in the evolution of CUB than currently believed and that the observed patterns of codon conservation observed by Akashi and others are likely due to other selective forces such as selection for translational efficiency or against nonsense errors.
Results
We began our analysis by first assuming that the abundance of a tRNA species within a cell is proportional to its gene copy number (GCN). This relationship between tRNA abundance and GCN is often made in studies of CUB and has been observed in both prokaryotes and eukaryotes [8], [31], [32]. We obtained GCNs of each tRNA type within an organism from the Genomic tRNA Database GtRNAdb [33] for 73 bacterial genomes representing 50 species from 20 genera (see Table S1 for list of genomes analyzed). We classified each amino acid based on its level of degeneracy , where represents the number of synonymous codons of that amino acid. As a result, each amino acid is placed in one of five different degenerate categories ). For instance, alanine belongs to the class, while lysine belongs to the class as these amino acids are coded by 4 and 2 codons, respectively. Serine represents a special case as it is encoded by two disjoint degenerate subsets. As a result we treated each of these subsets as a separate amino acid. We calculated the correlation between GCN of a focal tRNA and the sum of GCNs of neighboring tRNAs that coded for a different amino acid and differed from the focal tRNA's anticodon by a single base-pair, (Table 1). Figure 1 shows the distribution of correlation coefficients between and for three degenerate classes of amino acids within each of the genomes we examined.
Fig. 1. Correlation between a focal tRNA's abundance and the abundance of its neighbors , across 73 prokaryotic genomes. 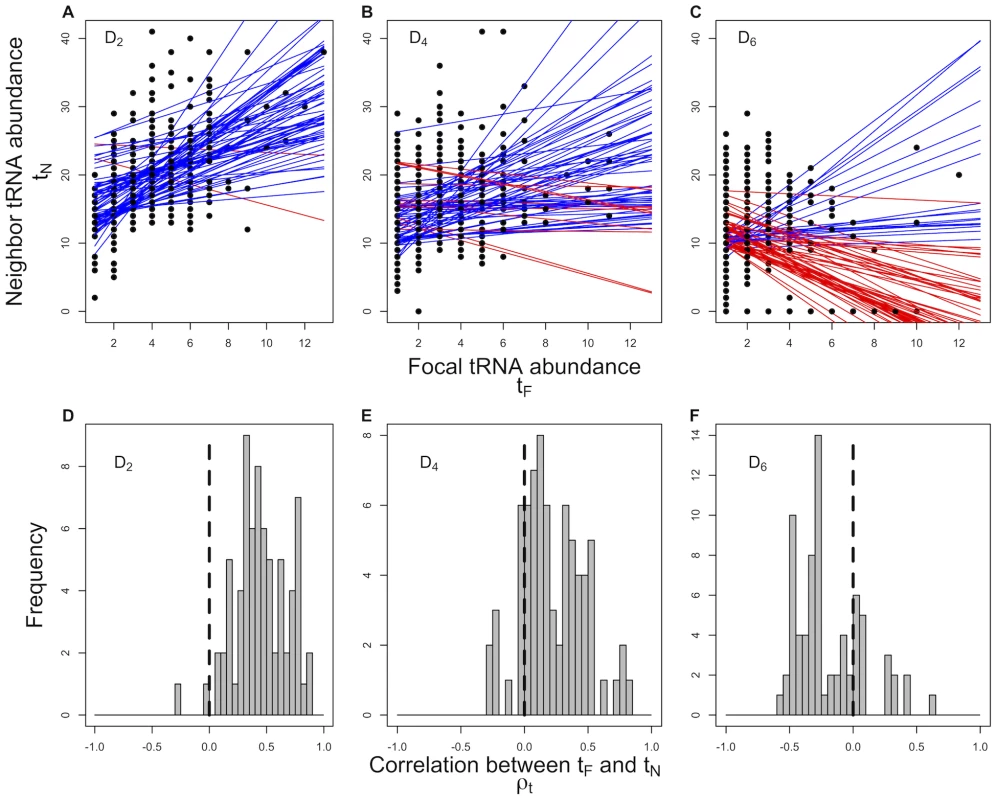
Each point in panels (A–C) represents a tRNA species that encodes an amino acid with degeneracy . The solid lines represent the regression lines between and for each genome. Genomes with a negative are coded in red, while genomes with a positive are represented by blue lines. Panels (D–F) present the distribution of correlation coefficients between and across all the genomes. The mean of the distribution of values for all the three degenerate classes differ significantly from 0 (Wilcox test, ). We find that the vast majority of genomes (69 out of 73 or ) show a positive relationship between the abundance of a focal tRNA species and its one-step non-synonymous neighbors , (Binomial test, , Figure S1). This indicates that tRNAs with similar abundances are closer to each other in the genetic code than expected under the implicit assumptions of the standard model. In other words, according to the standard model the tRNA abundances within the genetic code are predicted to be uncorrelated and the distributions of correlation coefficients in Figures 1 (d)–(f) are expected to be centered around . However, we find that under each of the degenerate classes of amino acids, , and , the distribution of is significantly different from (Wilcox test, ). Interestingly, we also find that the distribution of differs considerably between degenerate classes of amino acids. tRNAs corresponding to amino acids in both and degenerate classes show a significant bias towards a positive correlation between and , whereas tRNAs in degenerate class are biased towards a negative correlation.
Since the frequency of amino acid usage within a genome is highly correlated with tRNA gene copy number (e.g. in E. coli , ), the observed correlations may be the indirect result of amino acid usage bias. In addition to amino acid usage biases, the stereochemistry of codon-anticodon interactions forbids the existence of certain tRNA types [34], potentially contributing to the observed positive correlation among tRNA abundances. In order to address these inherent constraints on the distribution of tRNAs within the genetic code, we randomly distributed tRNA gene copies taking into account the stereochemical constraints, both with and without biased amino acid usage (see Figures S3 and S4). We find that the observed distribution of is significantly different from this more complex null distribution for all of the degenerate classes (Kolmogorov-Smirnov test for all cases).
The distribution of tRNAs within the genetic code have important consequences with respect to translation errors and bias in codon usage. Codons with higher tRNA abundances than their coding synonyms are often referred to as ‘optimal’ codons [10] assuming they lead to fewer translation errors [12], [25], [35]. In light of the above results, we now ask the question, “Given that tRNA abundances are positively correlated in the genetic code, do higher cognate tRNA abundances always lead to fewer translation errors?”
Modeling translation errors
Following [29], our model of translation errors takes into account competition between cognate and near-cognate tRNAs for the ribosomal A-site during translation. We also consider the kinetics of tRNA selection within a ribosome [27] and the effect of codon-anticodon wobble on these kinetics [36]. During protein translation, when a ribosome waits at a given codon, one of three outcomes is likely to occur: (a) elongation by cognate tRNA, (b) elongation by a near-cognate tRNA leading to a missense error or (c) spontaneous ribosomal drop-off, frameshift or recognition by release factors, any of which will lead to a nonsense error (Figure 2). The relative frequency of each of these outcomes determines the rates of missense and nonsense errors at a particular codon.
Fig. 2. Model of translation errors. 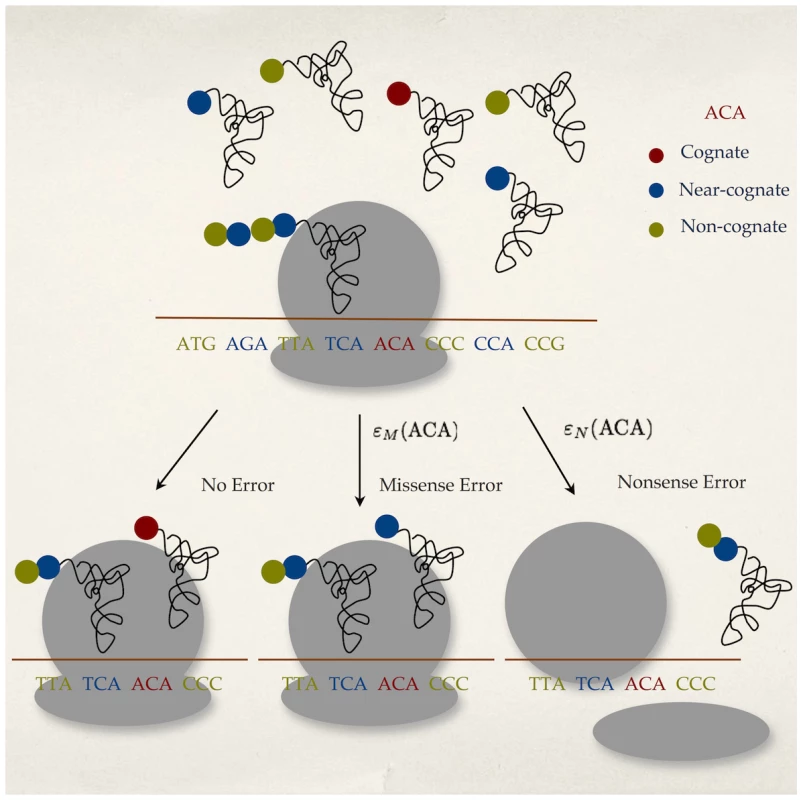
During translation, a ribosome pauses at a codon (ACA in this case) waiting for a cognate tRNA. During this pause, one of the three processes can take place: elongation by cognate tRNAs leading to no translation error, elongation by a near-cognate tRNA leading to a missense error with rate or premature termination of translation due to recognition by release factors, spontaneous ribosome drop-off or frameshifting leading to a nonsense error with a rate . Assuming an exponential waiting process for a tRNA at codon , the codon specific missense and nonsense error rates, and respectively, can be calculated as follows,(1)(2)where is the codon specific cognate elongation rate, is the codon specific near-cognate elongation rate, and represents the background nonsense error rate (see Methods for details).
Using Equations (1) and (2), we calculated codon-specific missense and nonsense error rates for each bacterial genome. In order to understand the effect of codon degeneracy on the relationship between error rates and codon elongation rates, we categorized amino acids based on the number of their synonymous codons as before. Given our model was parametrized from data on E. coli, we also checked for the sensitivity of our analysis to changes in these parameters when extending it to other prokaryotes (Text S1 B).
Error rates vs. elongation rates
Using E. coli strain K12/DH10B (K12) as an example, our estimates of codon-specific missense error rates ranged from with a median of . Six of the 61 sense codons have a predicted missense error rate of as these codons have no near-cognate tRNA species (Table S2). These rates are higher than recent empirical estimates of missense error rates in E. coli, which vary from with a median value of [25]. This is likely due to the fact that the missense error estimates in [25] were for specific amino acid misincorporations, whereas, the values predicted here indicate the rate of all possible missense errors at a given codon. Our predicted rates of codon-specific nonsense errors in E. coli ranged from with a median of (Table S2).
We find that on average both missense and nonsense error rates decrease with an increase in cognate elongation rates (Figure 3). These results seem, on first glance, largely consistent with the standard model for inferring translation errors from tRNA abundances, which assumes that decreases with . However, because varies between synonymous codons, for about half of the amino acids (10 out of 21) is actually greater for the codon with the highest value. This holds even when empirical estimates of tRNA abundances in E. coli [31] are used instead of tRNA gene copy numbers (see Figure S5). This result is inconsistent with expectations under the standard model that implicitly assumes a codon-independent rate of elongation by near-cognate tRNAs, . If the abundance of a focal tRNA and its neighbors are uncorrelated, then the only factor that affects is . However, as shown earlier, and are positively correlated (Figure 1). Thus, the estimates of of synonymous codons of an amino acid depend not only on their individual but also on the slope of the relationship between and . If the rate of increase of with is higher than the relative increase in , then codons with higher cognate elongation rates are expected to have higher missense error rates (Figure S2). Interestingly, 8 out of the 10 amino acids in E. coli K12 showed a positive relationship between and . Specifically, we would expect to increase with whenever the condition is satisfied. Thus, among the synonymous codons of an amino acid in E. coli, the codon with the lowest is often not the codon with the highest . This points to a fundamental change in our understanding of the relationship between tRNA abundances and missense errors and which codons minimize their occurrence.
Fig. 3. Correlation of translation error rates with cognate elongation rate in E. coli. 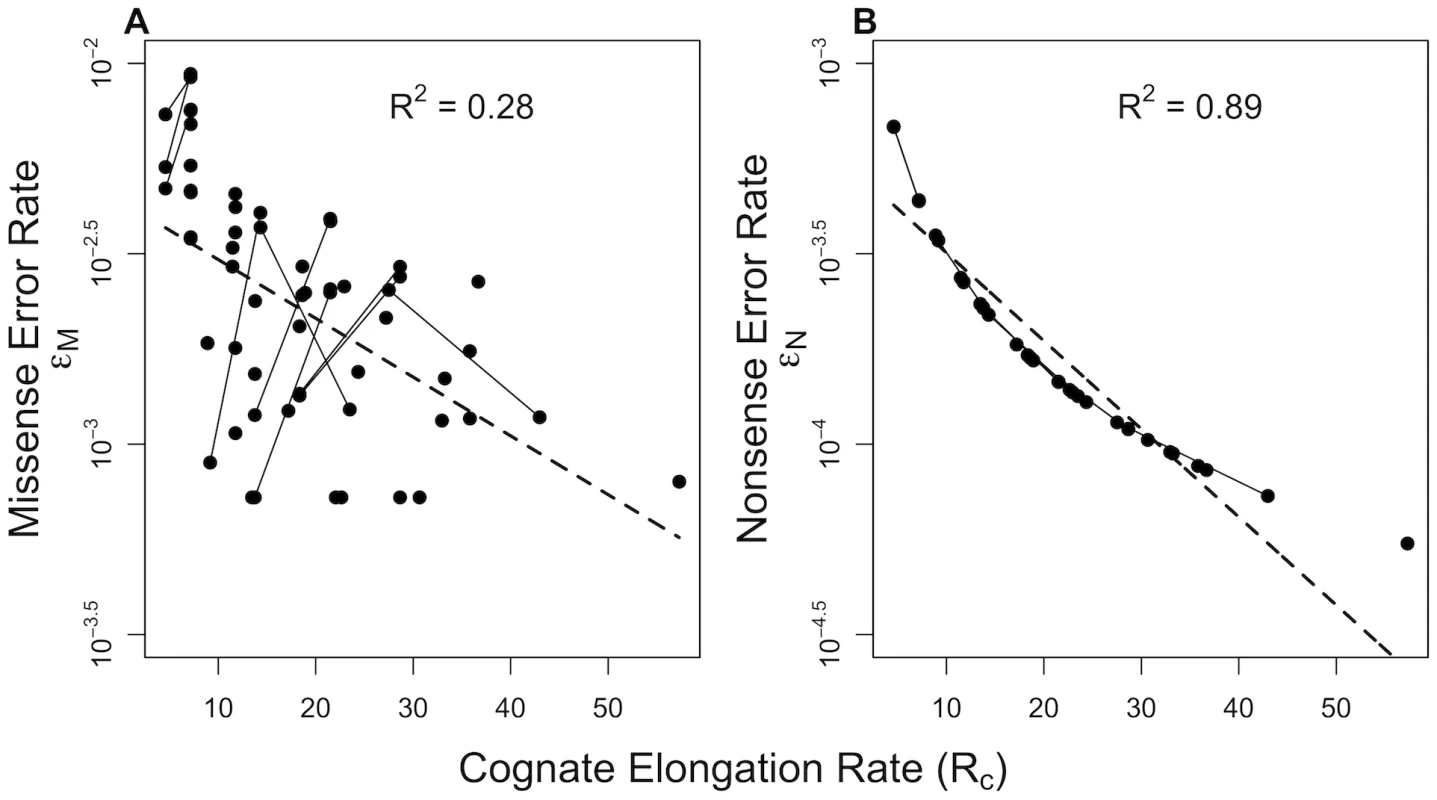
We find that rates of both (A) missense and (B) nonsense errors are negatively correlated with the rate of elongation by cognate tRNAs at that codon. The dashed line indicates the regression line between and . This is consistent with expectations under the standard model. However, in the case of twofold degenerate amino acids (), whose two codons are joined together by solid lines, we see that increases with for 8 out of 10 amino acids. In the case of every amino acid showed a decrease in with . Interestingly, these results are also consistent with the limited empirical estimates of codon-specific missense error rates. For instance, [22] used E. coli to estimate rates at which the asparagine codons AAC and AAU were mistranslated by . As expected, the authors found that the AAC codon, with a higher had a lower rate of mistranslation by than AAU, with a lower . Our model makes the same prediction when considering this specific subset of missense errors. However, when considering the overall missense error rates at AAC and AAU codons due to , , , , , and (all one-step neighbors), we come to a very different prediction. Specifically we find that even though AAC has a higher than AAU, it also has a much higher rate. As a result, the overall missense error rate for AAC is actually predicted to be higher than AAU. This result illustrates how focusing on only a subset of possible missense errors at a codon, as all previous experiments have done, provides an incomplete and potentially misleading picture.
In contrast to missense error rates, our model predicts will consistently decline with an increase in , suggesting that nonsense errors may be playing a larger role in driving CUB than commonly accepted [14].
Intra - and inter-specific variation in the relationship between elongation and error rates
In order to evaluate the relationship between cognate elongation rate, , and error rates, we looked across 73 bacterial genomes for inter-specific variation and 11 strains of E. coli for intra-specific variation. As before, we categorized amino acids based on the degeneracy of their synonymous codons for each genome. We calculated the fraction of amino acids within each category that showed a negative relationship between and error rates, and (Figure 4) as expected under the standard model where the abundances of tRNAs are assumed to be uncorrelated.
Fig. 4. Frequencies of negative relationships between cognate elongation rate and translation errors . 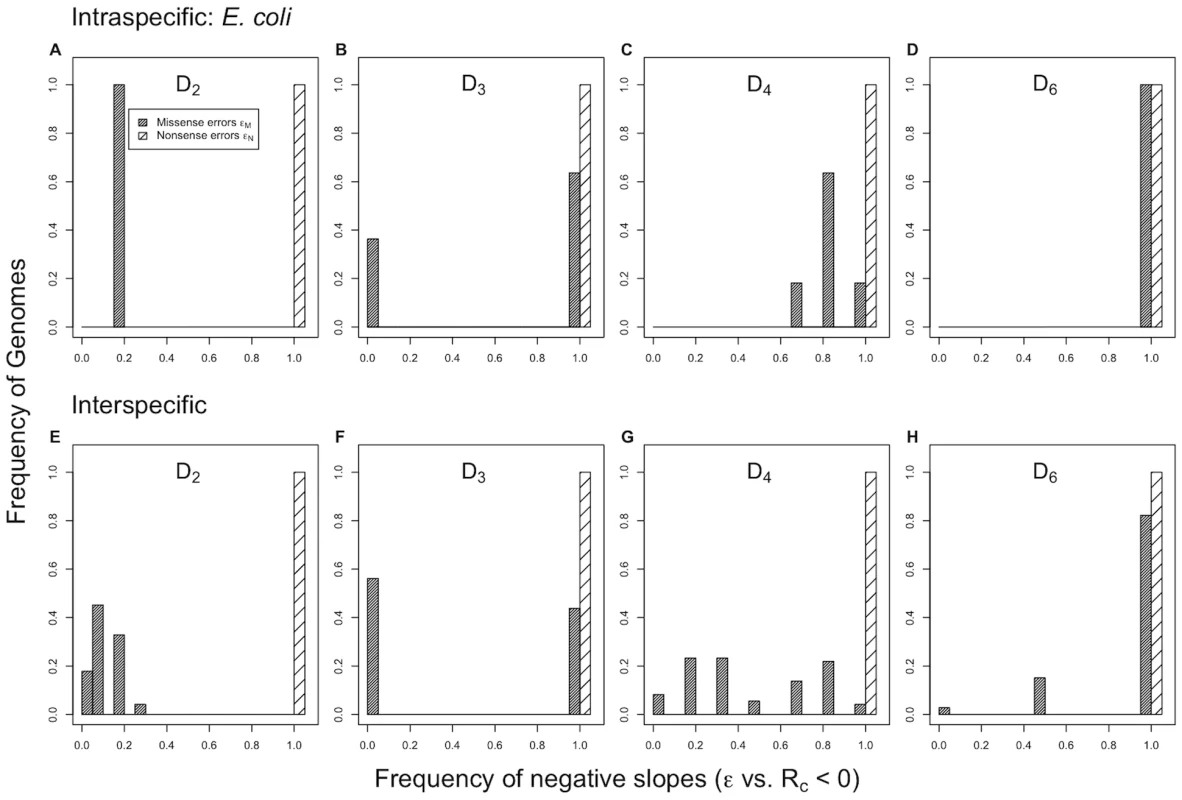
Panels (A–D) represent the distribution of E. coli strains that show amino acid specific negative relationship between and , while panels (E–H) represent the distribution of 73 genomes for the same. Amino acids in every degenerate class () show a negative relationship between cognate elongation rate and nonsense error rates () both intra-specifically as well as inter-specifically. A majority of amino acids in the 2-fold degenerate class () show an increase in missense error rate with across genomes. As the degeneracy of amino acids increases, we see an increase in the frequency of the expected negative relationship between and across E. coli strains as well as other bacterial species. For both intra - and inter-specific datasets we find that synonymous codons with a higher have a lower nonsense error rate for all amino acids, irrespective of the degenerate class they belong to. However, in the case of missense errors, the relationship between and depends on the amino acid degeneracy as previously observed in E. coli K12 (Figure 3). Amino acids with two synonymous codons () show a strong bias towards a positive relationship between and , both intra - and inter-specifically (Binomial test, and , respectively). In the case of isoleucine, the only amino acid in , there exists no bias towards a positive or a negative relationship between cognate elongation and missense error rates (Binomial test, intra-specific and interspecific ). Interestingly 4-fold degenerate amino acids show a bimodal distribution of the fraction of genomes with a negative relationship, and the two 6-fold degenerate amino acids (arginine and leucine) show a strong bias towards negative correlation between and (Binomial test, intra-specific and interspecific ). The differences in the relationship between and across degenerate classes are similar to the differences in the correlation between and across these classes (Figure 1).
Although the patterns we observe are complex and vary with amino acid degenerate classes, the assumption underlying the standard model that higher cognate tRNA abundance codons will have the lowest translation error rates is predicted to be clearly violated in the case of missense errors – a finding consistent both across bacterial genomes and across various E. coli strains. We also find that the positive relationship between missense error rates and observed within certain amino acids is insensitive to moderate changes in parameter estimates of background nonsense error rates, and wobble parameters (Text S1 B).
Discussion
For over 30 years, the standard model of translation errors has implicitly assumed that for any given amino acid, the translation error rates are lowest for the codons with the highest tRNA abundances [25], [26], [37]. With respect to missense errors , this prediction was based on the implicit and unstated assumption that the distribution of tRNA abundances across the genetic code are uncorrelated. Here we show a consistent positive correlation between the abundance of a tRNA and its one-step mutational neighbors across a wide array of prokaryotes. In order to understand the effects of this relationship on translation errors, we developed a simple model for estimating codon-specific error rates based on the distribution of tRNA gene copy number of a species. Our model takes into account tRNA competition, wobble effects, and intra-ribosomal kinetics of elongation to predict rates of missense and nonsense errors. To our knowledge, ours is the first model to integrate all these factors for estimating translation errors. Using our model, we find that on average, both missense and nonsense error rates of a codon decrease with an increase in its cognate tRNA elongation rate. This average behavior is consistent with expectations under the standard model of how codon specific error rates scale with cognate tRNA abundance [12], [15], [25], [38]. However, the expected relationship between error rates and cognate tRNA abundances does not hold at finer scales of individual amino acids, the relevant scale for the evolution of CUB.
For about half of the amino acids (10 out of 21) in E. coli K12, synonymous codons that have higher cognate elongation rates also have higher missense error rates . This counterintuitive behavior is due to the fact that tRNA abundances within the genetic code are positively correlated, which leads to an increase in with , an important pattern that has been overlooked by previous researchers. We find a positive correlation between the abundance of a focal tRNA and that of its neighbors in 69 out of 73 genomes examined here. In addition, the 4 genomes that show a negative (E. coli O157H7, E. coli O157H7-EDL933, Photobacterium profundum SS9, Vibrio parahaemolyticus) also show evidence of a high degree of horizontal gene transfer. Interestingly we also find that the differences in the relationship between and across amino acid degenerate classes is mirrored in the correlation between and . In contrast to , the nonsense error rates of synonymous codons decrease with an increase in for every amino acid across every genome we analyzed. This is due to the fact that increasing either or leads to a decrease in ribosomal wait time at that codon which, in turn, leads to a lower . Thus with respect to , a positive correlation between tRNA abundances actually accentuates the advantage of using codons with higher tRNA abundances. These results lend further support to the hypothesis that nonsense errors play an important but under-appreciated role in the evolution of CUB [11], [39].
The role of tRNA competition has been recognized as an important factor in affecting translation error rates [25], [26], [29]. However, previous studies on the relationship between error rates and tRNA abundances have focused primarily on the effects of modifying cognate tRNA abundances and ignored the effects of near-cognate tRNA abundances. Consistent with our model behavior, [25] showed that when was over-expressed, it led to a decrease in the missense error rate at codons for which the tRNA was a cognate: AGA and AGG. However, if a higher expression level of reduces the frequency of at codons AGA and AGG, why is it not fixed in the population? We argue that increasing the abundance of a given tRNA may not always be adaptive. For instance, over-expressing will also lead to an increase in at nearby non-synonymous codons - AAA, ACA, AUA, etc., a testable prediction not considered by [25]. The trade-offs between reducing at one codon at the expense of increasing at nearby codons has not been explored. However, these trade-offs likely play an important role in shaping the evolution of tRNA gene copy number and force us to reconsider the evolutionary causes of CUB.
Currently, many researchers believe that selection for translational accuracy, i.e., against missense errors, is a primary force driving the evolution of CUB (see [12], [14], [15], [40]). This belief largely rests on the interpretation of two facts. Firstly, preferred codons are generally those with the highest corresponding tRNA abundances and secondly, sites that are highly conserved and thought to have large effects on protein structure and function, use preferred codons more often than their coding synonyms [12]. Selection for translational accuracy is usually tested using Akashi's test by identifying evolutionarily conserved sites in protein sequences and checking whether they are coded by preferred codons [10], [12], [15], [41]. In light of the above results, we need to revisit the underlying assumptions of Akashi's test [12]. Although, our analysis predicts that a considerable number of amino acids have a positive relationship between missense error rates, and cognate elongation rates , many amino acids in are still predicted to conform to the standard model of lower with higher . Indeed, in the case of Drosophila species used in the original Akashi's paper [12], only 4 out of 21 amino acids are predicted to have a positive relationship between and . Thus, we argue that the relationship between and are highly species and amino acid specific and that selection for translation accuracy cannot explain all of the observed CUB at conserved sites. In addition to selection for translational accuracy, selection against nonsense errors [11], [39], [42], mRNA stability [6] and protein misfolding due to ribosome stalling [43], [44] have been shown to affect CUB. In fact, recent evidence suggests that the speed of translating a codon also affects protein folding [43]–[45]. The presence of a codon with a low , increases the ribosomal waiting time at a codon potentially leading to alternate protein folds. This directly affects the functionality and stability of the protein. Thus, a codon with a higher at a conserved site, as observed by Akashi and others, could be under selection to prevent protein misfolding due to an entirely different mechanism unrelated to missense errors. Thus, we would like to stress that the definition of preferred codons used in the Akashis test is based on the genome-wide frequency of codon usage and not on any fundamental biological process. Although, we do not dispute the fact that certain codons are preferred over others at conserved sites, we simply point that the presence of these preferred codons at conserved sites cannot be explained entirely by selection against missense errors and that other selective forces must be responsible for the maintenance of these codons.
CUB often increases with gene expression, such that highly expressed genes tend to use codons with a higher cognate elongation rate [11], [35], [46]. Thus, these genes would have lower nonsense error rates and wait times, but not necessarily lower missense error rates. This might appear paradoxical, as the failure to minimize missense error rate would presumably increase the probability that a translated protein would be rendered nonfunctional and be selected against. However, the deleterious effects of a high missense error rate can be mitigated by an increased robustness of highly expressed genes. According to [40], [47], [48], highly expressed genes are expected to evolve at a slower rate and also be extremely functionally robust to missense errors. If this is the case, then missense errors in highly expressed genes may not have much of an effect on protein function. These genes maybe perfectly poised for trading off an elevated missense error rate for faster elongation and fewer nonsense error rates.
When it comes to mitigating the effects of non-synonymous mutations and missense errors, the genetic code has been described as “one in a million” [17]. This is due to the fact that amino acids with similar chemical properties are in a genetic ‘neighborhood’, thus reducing the phenotypic effect of any point mutation or missense error. However, unlike point mutations, the frequency of missense errors depends on the distribution of tRNA within the genetic code. The distribution of tRNA abundances is usually attributed to the coevolution between codon usage and tRNA abundances [49]–[51]. However, these studies have not taken into account how changes in tRNA abundances affect the rate of translation errors at neighboring codons. The degree to which the distribution of tRNA abundances within the genetic code is adapted to minimize translation errors remains largely unexplored. Our work suggests that understanding the trade-offs between missense and nonsense errors would provide significant insights into the evolution of tRNA abundances within the genetic code. We believe building mechanistic models of translation errors, as shown here, will help further our understanding of the evolution of tRNA abundances across the genetic code.
Methods
tRNA competition
Assuming an exponential waiting process and simple diffusion, the rates at which cognate and near-cognate tRNAs enter the ribosomal A-site will be proportional to their abundances. As a result, translation error rates of a codon will depend, in part, on the relative abundances of its cognate and near-cognate tRNAs [25]. Following [8], [31], [32], we use the GCN of a tRNA as a proxy for its abundance.
Intra-ribosomal dynamics
Discrimination between cognate, near-cognate and non-cognate tRNAs takes place in the peptidyl transfer step of elongation. Since the underlying process is stochastic, there is a non-zero probability that when a cognate tRNA enters the A-site it will be rejected or a near-cognate tRNA will be accepted [27]. These probabilities are a function of the kinetic rate constants of various steps involved within the peptidyl transfer and translocation processes during tRNA elongation for both cognate and near-cognate tRNAs [27], [52], [53] (Text S1 A). Based on the rate constants for cognate and near-cognate tRNAs from [27] and equations from [29], we estimated the probability of elongation of a codon by a cognate and near-cognate tRNA per tRNA entry into the ribosomal A-site to be and , respectively (Text S1 A).
Wobble effects
One of the factors affecting the rate constants in the intra-ribosome kinetic model described above, is the effect of codon-anticodon wobble. [27] proposed that a wobble mismatch between a codon and its cognate tRNA anticodon, will affect its kinetic rate constants (Text S1 A) and consequently reduce the probability of elongation by that tRNA. Based on [34], [36], we assume that a purine-purine or pyrimidine-pyrimidine wobble reduces the probability of a cognate tRNA being accepted , by 40%. This reduction in is consistent with estimates based on the kinetic rate constants estimated by [54] for codon that is recognized by through a pyrimidine-pyrimidine wobble. Similarly, based on [36] ,we assume that a non-canonical purine-pyrimidine wobble (GU/AC) would reduce by 36%.
In addition, some codons can be recognized by cognate tRNAs through a non-standard wobble as described by [55], [56]. For instance, C-U and C-A anticodon-codon interactions are considered nonstandard owing to their stereochemistry and thermodynamic constraints. Hence, even though anticodon does not lead to a missense error when translating the codon , it is considered nonstandard translation due to its C-U wobble. We call these tRNAs ‘pseudo-cognates’. We assume that the probability of elongation of a codon by pseudo-cognates is the same as that of near-cognate tRNAs, i.e., .
Estimation of cognate and near-cognate elongation rates
In order to predict per codon missense and nonsense error rates, we calculated the rates of elongation by cognate and pseudo-cognate tRNAs vs. near-cognate tRNAs at each codon. The cognate elongation rate for codon is given by(3)where is the set of cognate tRNAs for codon , represents the set of pseudo-cognate tRNAs, represents the gene copy number of tRNA species, and is the reduction in elongation probability due to wobble mismatch.
Similarly, the rate at which near-cognate tRNAs elongate codon is given by(4)where is the set of near-cognate tRNAs with respect to codon . The parameter a represents a scaling constant between tRNA gene copy number GCN and elongation rate. For E. coli, we used a value of , so that the harmonic mean of elongation rates of all codons was [20], [26], [57].
We assume that nonsense errors occur primarily due to spontaneous drop-off of ribosomes at a given codon when it is waiting for a tRNA. As a result, the nonsense error rate due to spontaneous ribosomal drop-off, , is codon independent and occurs at a constant rate. [24] measured a nonsense error rate of per codons. If we assume , then the background rate of nonsense errors is .
Supporting Information
Zdroje
1. LobleyGE
MilneV
LovieJM
ReedsPJ
PennieK
1980 Whole body and tissue protein synthesis in cattle. Br J Nutr 43 491 502
2. PannevisMC
HoulihanDF
1992 The energetic cost of protein synthesis in isolated hepatocytes of rainbow trout (oncorhynchus mykiss). J Comp Physiol B, Biochem Syst Environ Physiol 162 393 400
3. WarnerJR
1999 The economics of ribosome biosynthesis in yeast. Trends Biochem Sci 24 437 40
4. AkashiH
GojoboriT
2002 Metabolic efficiency and amino acid composition in the proteomes of Escherichia coli and Bacillus subtilis. Proceedings of the National Academy of Sciences of the United States of America 99 3695 700
5. SharpPM
LiWH
1986 An evolutionary perspective on synonymous codon usage in unicellular organisms. J Mol Evol 24 28 38
6. BulmerM
1991 The selection-mutation-drift theory of synonymous codon usage. Genetics 129 897 907
7. BergOG
KurlandCG
1997 Growth rate-optimised tRNA abundance and codon usage. Journal of Molecular Biology 270 544 50
8. KanayaS
YamadaY
KudoY
IkemuraT
1999 Studies of codon usage and tRNA genes of 18 unicellular organisms and quantification of Bacillus subtilis tRNAs: gene expression level and species-specific diversity of codon usage based on multivariate analysis. Gene 238 143 55
9. RochaEPC
2004 Codon usage bias from tRNA's point of view: redundancy, specialization, and efficient decoding for translation optimization. Genome Research 14 2279 86
10. DrummondDA
WilkeCO
2009 The evolutionary consequences of erroneous protein synthesis. Nat Rev Genet 10 715 24
11. GilchristMA
ShahP
ZaretzkiR
2009 Measuring and detecting molecular adaptation in codon usage against nonsense errors during protein translation. Genetics 183 1493 505
12. AkashiH
1994 Synonymous codon usage in Drosophila melanogaster: natural selection and translational accuracy. Genetics 136 927 35
13. AkashiH
2001 Gene expression and molecular evolution. Current Opinion in Genetics & Development 11 660 6
14. AravaY
BoasFE
BrownPO
HerschlagD
2005 Dissecting eukaryotic translation and its control by ribosome density mapping. Nucleic Acids Research 33 2421 32
15. StoletzkiN
Eyre-WalkerA
2007 Synonymous codon usage in Escherichia coli: selection for translational accuracy. Molecular Biology and Evolution 24 374 81
16. GranthamR
1974 Amino acid difference formula to help explain protein evolution. Science 185 862 4
17. FreelandSJ
HurstLD
1998 The genetic code is one in a million. J Mol Evol 47 238 48
18. FreelandSJ
KnightRD
LandweberLF
HurstLD
2000 Early fixation of an optimal genetic code. Molecular Biology and Evolution 17 511 8
19. HiggsP
2009 A four-column theory for the origin of the genetic code: tracing the evolutionary pathways that gave rise to an optimized code. Biol Direct 4 16
20. AnderssonDI
BohmanK
IsakssonLA
KurlandCG
1982 Translation rates and misreading characteristics of rpsd mutants in Escherichia coli. Mol Gen Genet 187 467 72
21. BouadlounF
DonnerD
KurlandCG
1983 Codon-specific missense errors in vivo. EMBO J 2 1351 6
22. PrecupJ
ParkerJ
1987 Missense misreading of asparagine codons as a function of codon identity and context. J Biol Chem 262 11351 5
23. KurlandCG
EhrenbergM
1987 Growth-optimizing accuracy of gene expression. Annual review of biophysics and biophysical chemistry 16 291 317
24. JørgensenF
KurlandCG
1990 Processivity errors of gene expression in Escherichia coli. Journal of Molecular Biology 215 511 21
25. KramerEB
FarabaughPJ
2007 The frequency of translational misreading errors in e.coli is largely determined by tRNA competition. RNA 13 87 96
26. VarenneS
BucJ
LloubesR
LazdunskiC
1984 Translation is a non-uniform process. effect of trna availability on the rate of elongation of nascent polypeptide chains. Journal of Molecular Biology 180 549 76
27. GromadskiKB
RodninaMV
2004 Kinetic determinants of high-fidelity tRNA discrimination on the ribosome. Mol Cell 13 191 200
28. OgleJM
BrodersenDE
ClemonsWM
TarryMJ
CarterAP
2001 Recognition of cognate transfer RNA by the 30S ribosomal subunit. Science 292 897 902
29. FluittA
PienaarE
ViljoenH
2007 Ribosome kinetics and aa-tRNA competition determine rate and fidelity of peptide synthesis. Computational Biology and Chemistry 31 335 46
30. ZaherHS
GreenR
2009 Fidelity at the molecular level: lessons from protein synthesis. Cell 136 746 62
31. DongH
NilssonL
KurlandCG
1996 Co-variation of tRNA abundance and codon usage in Escherichia coli at different growth rates. Journal of Molecular Biology 260 649 63
32. CognatV
DeragonJM
VinogradovaE
SalinasT
RemacleC
2008 On the evolution and expression of Chlamydomonas reinhardtii nucleus-encoded transfer RNA genes. Genetics 179 113 23
33. ChanPP
LoweTM
2009 GtRNAdb: a database of transfer RNA genes detected in genomic sequence. Nucleic Acids Research 37 D93 7
34. LimVI
CurranJF
2001 Analysis of codon:anticodon interactions within the ribosome provides new insights into codon reading and the genetic code structure. RNA 7 942 57
35. IkemuraT
1985 Codon usage and tRNA content in unicellular and multicellular organisms. Molecular Biology and Evolution 2 13 34
36. CurranJF
YarusM
1989 Rates of aminoacyl-tRNA selection at 29 sense codons in vivo. Journal of Molecular Biology 209 65 77
37. IkemuraT
1981 Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: a proposal for a synonymous codon choice that is optimal for the e.coli translational system. Journal of Molecular Biology 151 389 409
38. DrummondDA
WilkeCO
2008 Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell 134 341 52
39. GilchristMA
2007 Combining models of protein translation and population genetics to predict protein production rates from codon usage patterns. Molecular Biology and Evolution 24 2362 72
40. DrummondDA
BloomJD
AdamiC
WilkeCO
ArnoldFH
2005 Why highly expressed proteins evolve slowly. Proc Natl Acad Sci USA 102 14338 43
41. DrummondDA
RavalA
WilkeCO
2006 A single determinant dominates the rate of yeast protein evolution. Molecular Biology and Evolution 23 327 37
42. GilchristMA
WagnerA
2006 A model of protein translation including codon bias, nonsense errors, and ribosome recycling. Journal of Theoretical Biology 239 417 34
43. Kimchi-SarfatyC
OhJM
KimIW
SaunaZE
CalcagnoAM
2007 A “silent” polymorphism in the mdr1 gene changes substrate specificity. Science 315 525 8
44. TsaiCJ
SaunaZE
Kimchi-SarfatyC
AmbudkarSV
GottesmanMM
2008 Synonymous mutations and ribosome stalling can lead to altered folding pathways and distinct minima. J Mol Biol 383 281 91
45. MarinM
2008 Folding at the rhythm of the rare codon beat. Biotechnol J 3 1047 57
46. GreenbaumD
ColangeloC
WilliamsK
GersteinM
2003 Comparing protein abundance and mRNA expression levels on a genomic scale. Genome Biol 4 117
47. KelloggE
JulianoN
1997 The structure and function of rubisco and their implications for systematic studies. American journal of botany
48. WilkeCO
DrummondDA
2006 Population genetics of translational robustness. Genetics 173 473 81
49. WongJT
1975 A co-evolution theory of the genetic code. Proc Natl Acad Sci USA 72 1909 12
50. ArdellDH
SellaG
2001 On the evolution of redundancy in genetic codes. J Mol Evol 53 269 81
51. VetsigianK
GoldenfeldN
2009 Genome rhetoric and the emergence of compositional bias. Proc Natl Acad Sci USA 106 215 20
52. BlanchardSC
KimHD
GonzalezRL
PuglisiJD
ChuS
2004 tRNA dynamics on the ribosome during translation. Proc Natl Acad Sci USA 101 12893 8
53. BlanchardSC
GonzalezRL
KimHD
ChuS
PuglisiJD
2004 tRNA selection and kinetic proofreading in translation. Nat Struct Mol Biol 11 1008 14
54. KotheU
RodninaMV
2007 Codon reading by tRNA-ala with modified uridine in the wobble position. Mol Cell 25 167 74
55. AgrisPF
1991 Wobble position modified nucleosides evolved to select transfer RNA codon recognition: a modified-wobble hypothesis. Biochimie 73 1345 9
56. AgrisPF
VendeixFAP
GrahamWD
2007 tRNA's wobble decoding of the genome: 40 years of modification. J Mol Biol 366 1 13
57. SørensenMA
KurlandCG
PedersenS
1989 Codon usage determines translation rate in Escherichia coli. Journal of Molecular Biology 207 365 77
Štítky
Genetika Reprodukční medicína
Článek Allelic Variation at the 8q23.3 Colorectal Cancer Risk Locus Functions as a Cis-Acting Regulator ofČlánek Allelic Selection of Amplicons in Glioblastoma Revealed by Combining Somatic and Germline AnalysisČlánek Lactic Acidosis Triggers Starvation Response with Paradoxical Induction of TXNIP through MondoAČlánek Rice a Cinnamoyl-CoA Reductase-Like Gene Family Member, Is Required for NH1-Mediated Immunity to pv.Článek Differentiation of Zebrafish Melanophores Depends on Transcription Factors AP2 Alpha and AP2 Epsilon
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2010 Číslo 9- Akutní intermitentní porfyrie
- Farmakogenetické testování pomáhá předcházet nežádoucím efektům léčiv
- Růst a vývoj dětí narozených pomocí IVF
- IVF a rakovina prsu – zvyšují hormony riziko vzniku rakoviny?
- Pilotní studie: stres a úzkost v průběhu IVF cyklu
-
Všechny články tohoto čísla
- Optimal Strategy for Competence Differentiation in Bacteria
- Mutational Patterns Cannot Explain Genome Composition: Are There Any Neutral Sites in the Genomes of Bacteria?
- Frail Hypotheses in Evolutionary Biology
- Genetic Architecture of Complex Traits and Accuracy of Genomic Prediction: Coat Colour, Milk-Fat Percentage, and Type in Holstein Cattle as Contrasting Model Traits
- Allelic Variation at the 8q23.3 Colorectal Cancer Risk Locus Functions as a Cis-Acting Regulator of
- Allelic Selection of Amplicons in Glioblastoma Revealed by Combining Somatic and Germline Analysis
- Germline Variation Controls the Architecture of Somatic Alterations in Tumors
- Mice Doubly-Deficient in Lysosomal Hexosaminidase A and Neuraminidase 4 Show Epileptic Crises and Rapid Neuronal Loss
- Analysis of Population Structure: A Unifying Framework and Novel Methods Based on Sparse Factor Analysis
- FliO Regulation of FliP in the Formation of the Flagellum
- Cdc20 Is Critical for Meiosis I and Fertility of Female Mice
- dMyc Functions Downstream of Yorkie to Promote the Supercompetitive Behavior of Hippo Pathway Mutant Cells
- DCAF26, an Adaptor Protein of Cul4-Based E3, Is Essential for DNA Methylation in
- Genome-Wide Double-Stranded RNA Sequencing Reveals the Functional Significance of Base-Paired RNAs in
- An Immune Response Network Associated with Blood Lipid Levels
- Genetic Variants and Their Interactions in the Prediction of Increased Pre-Clinical Carotid Atherosclerosis: The Cardiovascular Risk in Young Finns Study
- The Histone H3K36 Methyltransferase MES-4 Acts Epigenetically to Transmit the Memory of Germline Gene Expression to Progeny
- Long- and Short-Term Selective Forces on Malaria Parasite Genomes
- Lactic Acidosis Triggers Starvation Response with Paradoxical Induction of TXNIP through MondoA
- Identification of Early Requirements for Preplacodal Ectoderm and Sensory Organ Development
- Orphan CpG Islands Identify Numerous Conserved Promoters in the Mammalian Genome
- Analysis of the Basidiomycete Reveals Conservation of the Core Meiotic Expression Program over Half a Billion Years of Evolution
- ETS-4 Is a Transcriptional Regulator of Life Span in
- The SR Protein B52/SRp55 Is Required for DNA Topoisomerase I Recruitment to Chromatin, mRNA Release and Transcription Shutdown
- The Baker's Yeast Diploid Genome Is Remarkably Stable in Vegetative Growth and Meiosis
- Chromatin Landscape Dictates HSF Binding to Target DNA Elements
- The APETALA-2-Like Transcription Factor OsAP2-39 Controls Key Interactions between Abscisic Acid and Gibberellin in Rice
- Accurately Assessing the Risk of Schizophrenia Conferred by Rare Copy-Number Variation Affecting Genes with Brain Function
- Widespread Over-Expression of the X Chromosome in Sterile F Hybrid Mice
- The Characterization of Twenty Sequenced Human Genomes
- The Genome of a Pathogenic : Cooptive Virulence Underpinned by Key Gene Acquisitions
- A Single Element Maintains Repression of the Key Developmental Regulator
- Identification of New Genetic Risk Variants for Type 2 Diabetes
- Effect of Correlated tRNA Abundances on Translation Errors and Evolution of Codon Usage Bias
- Evidence of Selection upon Genomic GC-Content in Bacteria
- Proteomic Changes Resulting from Gene Copy Number Variations in Cancer Cells
- Rice a Cinnamoyl-CoA Reductase-Like Gene Family Member, Is Required for NH1-Mediated Immunity to pv.
- Longitudinal Genome-Wide Association of Cardiovascular Disease Risk Factors in the Bogalusa Heart Study
- Response to Mechanical Stress Is Mediated by the TRPA Channel Painless in the Heart
- DNMT3L Modulates Significant and Distinct Flanking Sequence Preference for DNA Methylation by DNMT3A and DNMT3B
- Identifying Signatures of Natural Selection in Tibetan and Andean Populations Using Dense Genome Scan Data
- Incremental Genetic Perturbations to MCM2-7 Expression and Subcellular Distribution Reveal Exquisite Sensitivity of Mice to DNA Replication Stress
- Loss of Maternal ATRX Results in Centromere Instability and Aneuploidy in the Mammalian Oocyte and Pre-Implantation Embryo
- Comparative Genomic Hybridization (CGH) Reveals a Neo-X Chromosome and Biased Gene Movement in Stalk-Eyed Flies (Genus )
- Differentiation of Zebrafish Melanophores Depends on Transcription Factors AP2 Alpha and AP2 Epsilon
- Gene–Environment Interactions at Nucleotide Resolution
- Dementia Revealed: Novel Chromosome 6 Locus for Late-Onset Alzheimer Disease Provides Genetic Evidence for Folate-Pathway Abnormalities
- Critical Functions of Rpa3/Ssb3 in S-Phase DNA Damage Responses in Fission Yeast
- Preferential Re-Replication of Heterochromatin in the Absence of Geminin
- The Potential for Enhancing the Power of Genetic Association Studies in African Americans through the Reuse of Existing Genotype Data
- Evidence That Mutation Is Universally Biased towards AT in Bacteria
- Perturbation Analysis of Heterochromatin-Mediated Gene Silencing and Somatic Inheritance
- Diversity of Eukaryotic DNA Replication Origins Revealed by Genome-Wide Analysis of Chromatin Structure
- Genetic Deletion of the Desmosomal Component Promotes Tumor Microinvasion in a Mouse Model of Pancreatic Neuroendocrine Carcinogenesis
- The Metabolic Enzyme ManA Reveals a Link between Cell Wall Integrity and Chromosome Morphology
- SNPs Associated with Cerebrospinal Fluid Phospho-Tau Levels Influence Rate of Decline in Alzheimer's Disease
- Synthesizing and Salvaging NAD: Lessons Learned from
- A Central Regulatory System Largely Controls Transcriptional Activation and Repression Responses to Phosphate Starvation in Arabidopsis
- An Insect Herbivore Microbiome with High Plant Biomass-Degrading Capacity
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Synthesizing and Salvaging NAD: Lessons Learned from
- Optimal Strategy for Competence Differentiation in Bacteria
- Long- and Short-Term Selective Forces on Malaria Parasite Genomes
- Identifying Signatures of Natural Selection in Tibetan and Andean Populations Using Dense Genome Scan Data
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání