Problém přípustných limitů preciznosti v regulačních diagramech

Souhrn

Cíl:
Korektní odvození přípustných limitů preciznosti pro správné nastavení regulačních diagramů a efektivní řízení interní kontroly kvality (IKK) v laboratorní praxi.

Metodika:
Aplikace 3-signální tabulky dle návrhu Haeckela a Wosnioka [1] pro výpočet přípustných limitů preciznosti z empirické biologické variability (CV_E) založené na referenčních intervalech a jejich následné použití pCV_A v regulačních diagramech.

Diskuse:
Možnosti použití 3-signální tabulky [1].

Závěr:
Varování před nesprávným použitím regulačních diagramů; správné odvození přípustných limitů mezilehlé preciznosti jako klíč pro efektivní použití regulačních diagramů a pro objektivní třídění jednotlivých laboratorních metod podle jejich kvality.

Klíčová slova:
přípustné meze preciznosti, třídy kvality, referenční meze, regulační diagramy.

Úvod

Mnoho autorů se zabývá vztahem mezi přípustnou hodnotou analytické preciznosti pCV_A a biologickou variabilitou CV_B. Volba, zda jako základ pCV_A použít CV_W, CV_G nebo CV_C, závisí na účelu vyšetření pacienta (diagnostika vs. monitorování) a požadovaná hodnota pCV_A by dle Cotlova pravidla neměla přesáhnout 0,5 CV_B, který požadovanou SD_A odvozoval z kombinované SD_C [2]. Nejznámější v českém odborném povědomí je Fraser [3], který za požadovanou CV_A uvádí 0,5 CV_W.

Alternativní koncept určení přípustných limitů preciznosti, které prezentoval Klee [4], bere v úvahu ztrátu diagnostické specifičnosti, která je způsobena analytickou variabilitou, a vyjadřuje se jako nárůst počtu falešně pozitivních výsledků (∆ FPR). Požadavek na preciznost vztaženou k podílu klinických chyb v podmínkách referenčních mezí navrhli již dříve Acland a Lipton [5]. Haeckel a Wosniok [1] z těchto návrhů vycházejí a předkládají kompromisní řešení zaměřené na stanovení pCV_A tak, aby bylo v dobrém souladu se stávající technickou proveditelností.

Terminologie a zkratky zde uvedené jsou v souladu se současnou terminologií VIM [6]. Preciznost měření je vyjádřena číselně mírami preciznosti (CV, SD), v textu je možné volně termíny zaměnit. Termín „přípustný” limit byl rovněž převzat z [6].

Metodika

K vnitřní kontrole kvality (dále jen IKK) se používají kontrolní materiály, které obvykle mají cílové hodnoty a SD jednotlivých měřených veličin vyšetřovaných analytů deklarované výrobcem. Tyto hodnoty je nutno před zařazením do interního kontrolního programu (IKK) ověřit stanovením v podmínkách konkrétní laboratoře.

Doporučený postup ověření mezilehlé preciznosti vychází z definice VIM [6] a je takový, že před použitím materiálu se všechny analyty měří po dobu 20 po sobě následujících dnů (n = 20). Z takto naměřených hodnot se po vyloučení odlehlých hodnot vhodným testem vypočte aritmetický průměr, směrodatná odchylka (SD) resp. příslušný variační koeficient v  % (CV) pro každou měřenou veličinu (parametr).

Reálné variační koeficienty mezilehlé preciznosti měřených veličin v klinické biochemii určené jako kovariance variačních koeficientů preciznosti z IKK na dvou nebo třech koncentračních hladinách analytů uvedl pod označením CV_A Jabor [7] v přehledných tabulkách, v nichž lze uvedené hodnoty CV_A zároveň porovnat s požadovanou precizností odvozenou z intraindividuální variability dle Frasera (viz výše). Údaje CV_A převedené do absolutních hodnot měřené veličiny čili hodnot SD, lze přímo použít v regulačních diagramech určených pro IKK příslušného analytického systému. Velikost CV_A je však dána pouze aktuálním stavem technické způsobilosti konkrétního analytického systému, a proto je nutné klinickou přijatelnost CV_A vždy také posuzovat i s ohledem na maximální povolenou chybu resp. aktuální maximální odchylku D_max odvozenou z cyklů externí kontroly kvality, např. SEKK [8]. Nevýhodou takové koncepce je, že takto získané hodnoty D_max [8,14] nemají žádný vědecký základ, nejsou orientované na lékařské potřeby a mnohdy nejsou transparentní, protože v nich obvykle chybí odkaz na data, z nichž vycházejí. Především však nezahrnují hledisko diagnostické efektivity s ohledem na požadovanou specifičnost dané metody.

Heackel a Wosniokova interpretace problému

Přípustné limity mezilehlé preciznosti pCV_A, které navrhli a v praktickém použití předvedli Haeckel a Wosniok [1], diagnostickou specifičnost dané vyšetřovací metody zohledňují, a navíc je lze použít i k odvození přípustných limitů EHK [8].

Hrubý odhad velikosti biologických variabilit odvozených z referenčních intervalů (dále jen RI), vyznačených mezemi RL_2,5 (2,5 % dolní limit) a RL_97,5 (97,5 % horní limit) tj. pro 95 % RI odvodil Tonks [10] v následujících krocích [2]:

Krok 1: RR₉₅ = referenční rozmezí = RL_97,5 - RL_2,5 (1)

Krok 2: MV = průměrná hodnota (RL_2,5 + RL_97,5)/2

s_E = RR₉₅/3,92 (2)

Krok 3: CV_E = (s_E x 100)/MV nebo (3)

CV_E = 25,51 x RR₉₅/MV (4)

kde CV_E je empirický (biologický) variační koeficient

a RI používané v rovnicích (1) – (4) lze získat buď z vnějších zdrojů po kontrole jejich přenositelnosti [11] nebo stanovit podle interních postupů buď přímo či nepřímo [12,13]

CV_E zahrnuje empirickou analytickou preciznost (CV_A) a z CV_E lze odhadnout CV_C:

CV_E = [(CV_C)² + (CV_A)²]^0,5 (5)

odtud také

CV_C = [(CV_E)² - (CV_A)²]^0,5 (6)

Při nulové hodnotě preciznosti činí dle definice počet falešně pozitivních výsledků FRP 2,5 % (RL_97,5); za přítomnosti preciznosti se hodnota FRP zvyšuje. Volba pěti tříd kvality měřených veličin se odvozuje z velikosti přírůstku počtu falešně pozitivních výsledků ∆FPR. Haeckel a Wosniok [1] ji implicitně stanovili následovně: ∆FPR = 0,2, 0,5, 1,0, 3,0, a 5,0  %. Horní limity tříd byly vypočteny jako podíly CV_A/CV_E odpovídající výše uvedeným apriori daným ∆FPR. Podíly CV_A/CV_E lze zhruba odhadnout pomocí rovnice (7) nebo za předpokladu Gaussova (normálního) rozložení referenčních hodnot přesně spočítat dle rovnic (9) a (10). Pro alternativní log-normální rozdělení referenčních hodnot, které je ale v praxi velmi časté, jsou výpočty jiné, které Hackel & Wosniok [1] uvádějí v dodatku.

Bylo zjištěno [1], že regresní funkce CV_A/CV_E má směrnici rovnou 0,413, odtud

CV_A/CV_E = 0,413 (∆FPR)^0,5 (7)

kde přibližný přírůstek FRP resp. ∆FRP odpovídá

∆FPR ≈ 5,86 (CV_A/ CV_E)² (8)

Za předpokladu normálního rozdělení referenčních dat a konstantní analytické směrodatné odchylky, se ∆FPR vypočítá podle rovnice (9) pro horní RL a (10) pro dolní RL:

∆FPR (RL_97,5) = 100-100xφ(RL_97,5, MV+bias, SE)-2,5 (9)

∆FPR (RL_2,5) = 100xφ(RL_2,5, MV+bias, SE)-2,5 (10)

kde φ označuje normální distribuční funkci.

Důkaz toho, že idea jediného požadovaného fixního podílu CV_A/CV_B dle Cotlova rovnajícímu se 0,5 CV_B, není reálná, poskytli právě Haeckel a Wosniok [1] pomocí bodového grafu, v němž na osu y vynesli podíly CV_A/CV_E a na osu x pozorované CV_A různých měřených veličin stanovených ve vybrané klinické laboratoři. Vynesené body vytvořily v grafu velký rozptýlený mrak kolem cílové přímky rovnoběžné s osou x kolmé k ose y ve vzdálenosti 0,5 od nuly. Za příčinu rozptýlenosti bodů označili autoři grafu velké rozdíly mezi stávajícími reálnými hodnotami podílů CV_A/CV_B a jedinou, předem pevně danou teoretickou 0,5 frakcí, čímž současně prokázali, že předpoklad univerzálního požadavku na přípustný limit pCV_A = 0,5 CV_B neodpovídá stupni současné technické způsobilosti měření většiny klinicko-biochemických veličin. Nově proto pro stávající měřené veličiny navrhli namísto jediné, fixní frakce 0,5 CV_B pět různých pCV_A, předem určených jako podíly empirické variability CV_E, a tím definovali pět různých tříd kvality viz Tabulka 1.

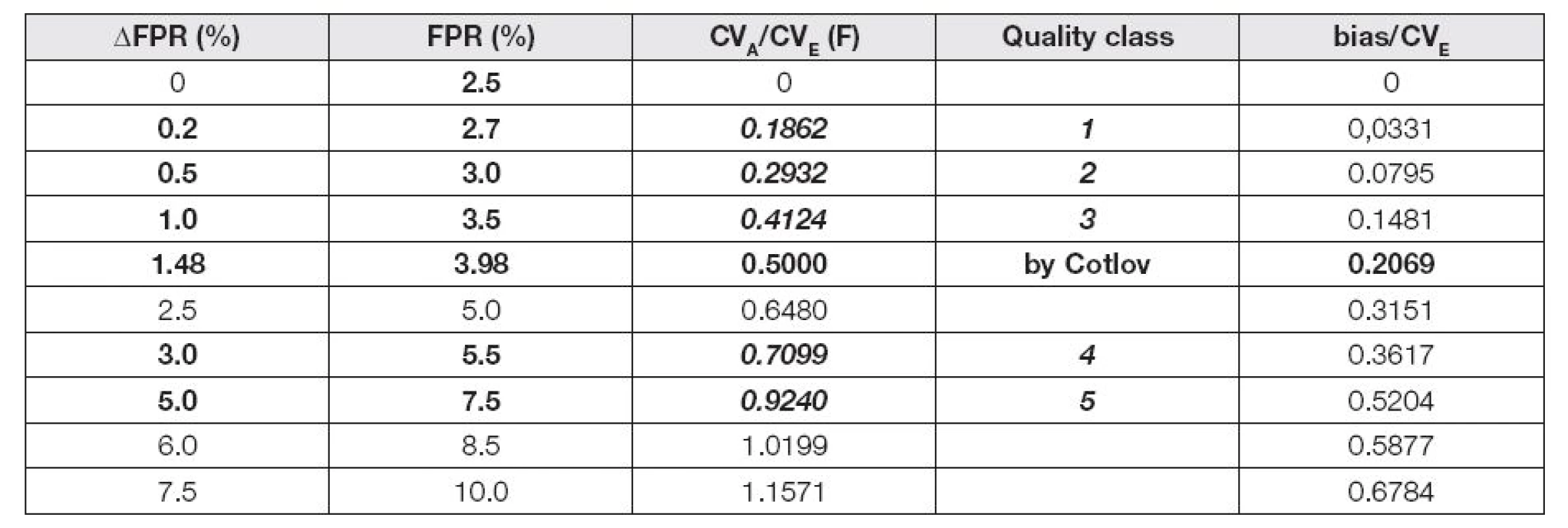
Diagnostická specifičnost metody klesá s rostoucím číslem třídy, z čehož vyplývá, že úsilí o zlepšení preciznosti analýzy by se mělo zaměřit především na metody umístěné ve třídách 4-5. V nepřítomnosti náhodných chyb se u měřených veličin umístěných ve třídách 1-3 zvýší FPR maximálně o 1,0  % (vztaženo k RL_97,5) a taková měření jsou považována za dostatečně přesná pro diagnostické účely.

Klasifikace měřených veličin do pěti kategorií poskytuje snadný přehled o laboratorních postupech, tedy o tom, zda mají vyšší či nižší teoretickou diagnostickou specifičnost (vyšší ∆FPR). Jako orientační pravidlo platí, že třída 1 obsahuje především měřené veličiny s poměrně vysokou hodnotou CV_B, a třída 5 analyty s velmi malou hodnotou CV_B. Pokud laboratoře neznají dolní RL_2,5 a je RI dán vztahem ≤ RL_97,5 a maximální hodnota CV_E = 51 (51,02) podle rovnice (4).

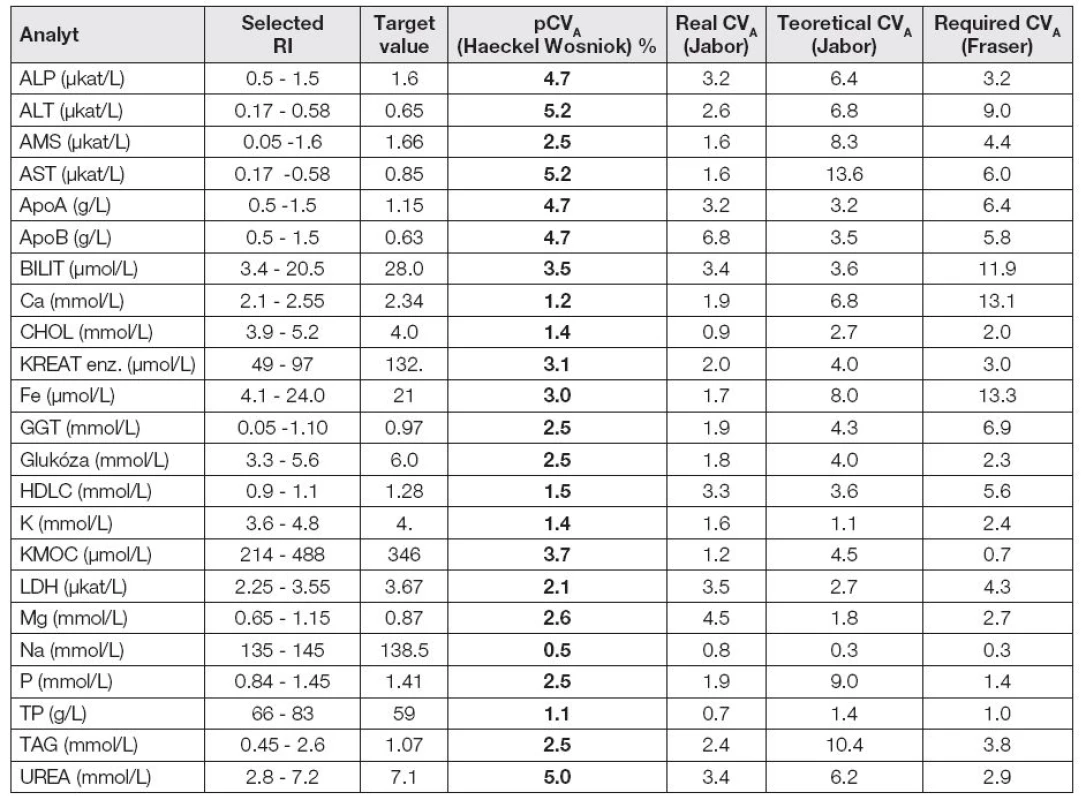
Postup vyplnění 3-signální tabulky

Haeckel a Wosniok [1] vytvořili na platformě programu v Excelu tzv. 3-signální tabulku (viz Tabulka 3) určenou k výpočtu přípustných limitů CV_A (pCV_A) a bias (pbias – zde jen pro účely EHK) v konkrétní laboratoři a k automatickému výběru třídy kvality dané měřené veličiny. Jako „3-signální“ je tabulka označována proto, že zvažuje hned několik důležitých aspektů: předem definované podíly biologické variability (jak navrhuje Fraser), počet falešně pozitivních výsledků (jak navrhoval Klee), a konečně, že zjištěnou provozní charakteristiku metody, hodnotu pCV_A, konvertuje na třídu kvality metody, zohledňující její stávající technickou proveditelnost. Tabulka tím svému uživateli poskytne nástroj pro rychlý přehled o diagnostické validitě všech zahrnutých kvantitativních postupů dané laboratoře.

Autoři konceptu [1] předvádějí práci s tabulkou na čtyřech listech Excelu, jež po sobě označují jako pracovní, ve druhém listu uvádějí příklady, třetí list obsahuje popis s legendou vysvětlující zkratky a funkčnost buněk tabulky a na čtvrtém listu je umístěna bezpečnostní záloha určená pro případ narušení či ztráty vložených výpočtů.

Druhý list obsahuje dva autorské příklady využití 3-signální tabulky „a)“ a „b)“. V části „a)“ prezentují autoři její využití pro hodnocení účasti v cyklech EHK a v části „b)“ k řízení IKK. Klíčový rozdíl obou těchto možností spočívá pouze v hodnotách pCV_A přisouzeným jednotlivým vyšetřovacím metodám ve sloupci F, kam se buď vyplňují fixní hodnoty stanovené příslušnou národní autoritou (např. Rilibäk, SEKK) nebo se do něj automaticky zkopírují aktuální výsledky pCV_A, vypočtené z hodnot CV_A zadaných uživatelem, zjištěných v rámci IKK. V případě využití tabulky jako nástroje řízení EHK vycházejí autoři z přístupu Německé národní příručky – Rilibäk [14], a to verze z r. 2003, která uváděla přípustné limity zvlášť pro maximální preciznost a zvlášť pro maximální vychýlení (bias).

3-signální tabulka umožňuje po řadě od sloupce A ke sloupci K zadat následující položky:

Název měřené veličiny - Dolní RL - Horní RL – Poznámka – Jednotky - pCV_A - CV_A - Třída - Cílová hodnota - Průměrná hodnota - Kód kontrolního materiálu. Sloupce mají v originální tabulce barevné podbarvení.

Laboratoř musí pouze vyplnit žlutá a hnědá pole (sloupce A-J). Žlutá pole povětšinou obsahují informace, které jsou obvykle vyžadovány pouze jednou (sloupce A-E), z nichž některé (např. referenční meze, sloupce B a C) nutné je aktualizovat jen, zavádí-li laboratoř nový měřící systém nebo jej modifikuje. Hnědá políčka (sloupec G, případně sloupce I, J pro EHK) je nutné pravidelně kontrolovat a aktualizovat, dojde-li ke změně analytické preciznosti nebo pravdivosti (např. po skončení kontrolního cyklu).

Hodnocení preciznosti (sloupce od O do Z) je naprogramováno tak, že uživatel jej následně může použít bez jakýchkoliv úprav. Od sloupce Z napravo jsou v buňkách obsaženy různé pomocné výpočty průměrné hodnoty, CV_E, podílů CV_A/CV_E, pCV_A/CV_E nebo výpočet pCV_A.

Aktuální, v laboratoři dosažený CV_A, příslušný dané měřené veličině, se zadává do sloupce G v předem určeném intervalu probíhajícího kontrolního cyklu IKK (např. každý měsíc), čímž se současně zobrazí jako zeleně podbarvená buňka některého ze sloupců L, N, P, R nebo T a program automaticky veličinu zařadí do jedné z výše zmíněných pěti tříd kvality (sloupce L až W). Jednotlivé třídy navzájem oddělují mezní hodnoty podílů CV_A/CV_E, které odpovídají předem zvoleným maximálním ∆FPR (viz výše). Algoritmus výpočtu volby přípustné třídy kvality (sloupec H) je spuštěn výpočtem poměru CV_A/CV_E a následující volbou: třída 1 je zvolena, pokud pCV_A/CV_E≤ 0,186, třída 2, je vybrána, pokud 0,186<CV_A/CV_E≤ 0,293 atd. Vybraná třída kvality měřené veličiny je pak zvýrazněna žlutým podbarvením příslušné buňky v některém ze sloupců M, O, Q, S nebo U. O umístění, kam hodnota padne, rozhoduje podíl pCV_A/CV_E čili v případě EHK fixní, národní autoritou stanovený pCV_A zatímco u IKK aktuální, vypočtená hodnota pCV_A kopírující se po výpočtu také vždy do žlutých buněk sloupce F.

Bias (rozdíl mezi cílovou a průměrnou hodnotou sloupce I a J) se vyjadřuje v % cílové hodnoty a případné jasně červené podbarvení sloupce W hlásí, že hodnota přesáhla přípustnou hodnotu (hodnoty pbias jsou v tomto konceptu číselně shodné s pCV_A).

Vyplní-li uživatel 3-signální tabulku podle přiloženého návodu, získá automaticky průběžný přehled o aktuálním stavu řízení EHK či IKK měřených veličin – viz níže Tabulku 3. zobrazující na malém příkladu dvou metod funkci obou částí 3-signální tabulky.

Diskuse ke správnému použití 3-signální tabulky

Hodnoty CV_A získané na základě doporučené 20denní analýzy vzorků kontrolních materiálů jsou mírou jejich průběžné celkové mezilehlé preciznosti (dále jen MP) a liší se od celkové MP stanovené při verifikaci laboratorní metody na vzorcích sér nebo plazmy tj. biologických materiálech humánního původu neurčených pro IKK. Rozdílnost celkových MP je mj. dána i volbou délky provádění testu MP, jež by měla být vždy volena i s ohledem na stabilitu a dostupnost daného testovaného materiálu v laboratorním provozu (celková MP zjišťovaná při verifikaci metody za období delší než činí doba, po kterou jsou humánní vzorky biologických materiálů běžně v dané laboratoři uchovávány, se jeví nejen z ryze praktického úhlu pohledu přinejmenším jako poněkud nepatřičná a často zbytečně navyšuje hodnotu nejistoty měření vzorků).

Cílové hodnoty uváděné výrobcem kontrolního materiálu lze použít pouze na počátku jeho použití k řízení IKK. Při prvním použití nového kontrolního materiálu nebo změně jeho šarže by vždy měl být proveden předběžný test cílený na zjištění hodnot celkové MP a ověření pravdivosti cílových hodnot uvedených výrobcem. Po provedení potřebného počtu startovních měření (např. 20denní měření paralelně s měřením kontrolního materiálu, jehož užívání končí) jsou vypočítány střední hodnoty a CV_A. Hodnocení pravdivosti, jejíž mírou je bias, je v 3-signální tabulce požadováno pouze za účelem mezilaboratorního porovnávání (EHK) a pokud jsou referenční meze cílových hodnot převzaty z externích zdrojů s definovaným bias (návazností).

Referenční meze byly v autorské verzi převzaty ze dvou zdrojů [15, 16]. Existuje-li pro danou měřenou veličinu více než jeden RI, pak autoři [1] doporučují pro získání co nejpřísnějšího pCV_A vybrat ten RI, který je nejužší a zajistí nejnižší hodnotu CV_E. Obecně platí, že by mělo být odvozeno tolik různých přípustných mezí odvozených od tolika různých RI, kolik je jich klinicky zapotřebí (pediatrické RI vs. RI pro dospělé), tedy s ohledem na cílové zaměření laboratoře. Každá laboratoř má mít své údaje o RI k dispozici, neboť je povinna je ověřovat a pravidelně přezkoumávat [17]. Autorka tohoto sdělení použila RI buď RI z [19] nebo uvedené výrobcem na základě analýzy dle [11]. Pokud laboratoře neznají dolní RL_2,5 a je RI dán ≤ RL_97,5, pak maximální hodnota CV_E = 51 (51,02) podle rovnice (4). Z důvodu docílení nižší CV_E se zde doporučuje dodatečně dolní RL_2,5 určit či pro daný účel převzít z literatury.

Standardizované CV_A (CV_A/CV_E) definují odpovídající třídu kvality. Po několika kontrolních cyklech je nutno rozhodnout, zda je pro laboratoř vhodná vyšší nebo nižší třída kvality, zvláště pokud je poměr CV_A/CV_E blízko k hranici třídy. Veličiny s CV_E ≥ 12 by neměly být ve třídě vyšší než 3, a veličiny s CV_E<12 by měly být alespoň ve třídě 4 nebo 5. Laboratoř má vždy usilovat o dosažení nižší třídy kvality, a tím zlepšení své diagnostické výkonnosti (lze zařadit mezi indikátory kvality).

Zásadní pravidlo nastavení regulačních diagramů vnitřní kontroly kvality

První vydání Westgardových „Basic QC Practices“ [18] je datováno 90. léty minulého století a odborníci předpokládají, že zásady v něm uvedené bezpečně zakotvily v povědomí několika generací klinických biochemiků, přesto však nekorektní praxe nastavování kontrolních limitů regulačních diagramů překvapivě nezřídka i v Čechách přetrvává dodnes. Zdá se, že absurdní příčinou může být prostá neznalost jednoho z klíčových doporučení [18, str. 67], a to následujícího:

Nepoužívat hodnot uvedených v příbalových letácích kontrolních materiálů pro IKK, protože základním principem statistické kontroly kvality (QC) je odhad stávající výkonnosti ve vztahu k výkonnosti předchozí a klíčovými mírami předchozí výkonnosti jsou průměr a SD výsledků měření kontrolního materiálu analyzovaného vaší metodou ve vaší laboratoři. Hodnoty SD přisouzené výrobci kontrolním materiálům odrážejí celkovou výkonnost zahrnuté skupiny laboratoří a mohou být pouze více či méně užitečným odhadem pravdivosti metody, nikoliv celkové preciznosti, neboť násobky SD výrobců obvykle poskytují kontrolní meze širší, než je žádoucí k efektivní kontrole kvality, a odtud nízký záchyt chyb.

V laboratorní praxi se zákazník prostřednictvím příbalových letáků obvykle setká s praxí, že výrobci kontrolních materiálů uvádějí cílové hodnoty měřených veličin, získané jako průměry sérií opakovaných měření a odpovídající SD (směrodatné odchylky výběru) těchto souborů dat (Westgardem zapovězené „lahvičkové“ SD). Poměrně často jsou také hodnoty SD nahrazovány limity možných hodnot, v lepším případě vztaženými ke konkrétnímu principu měření či definovanému analytickému systému. Někteří zástupci výrobců kontrolních materiálů v takovém případě běžně poskytují uživatelům zcela nevhodný návod, jak si hodnoty SD bez potřebného ověření v dané laboratoři zajistit: rozsah možných hodnot (horní RL- dolní RL) doporučují dělit čtyřmi, případně šesti s tím, že celé rozmezí představuje čtyř resp. šestinásobek SD originálního souboru dat za předpokladu rovnoměrného resp. triangulárního rozložení dat. Před použitím SD výrobců Westgard v rámci IKK důrazně varuje a po jejich přepočtu na %CV lze snadno zjistit proč.

S ohledem na klíčovou úlohu v řízení IKK by v regulačních diagramech měly figurovat pouze vlastní, verifikací ověřené specifikace měřené veličiny, a to jak cílové hodnota, tak především vlastní SD, které následně zajistí, že tyto grafické nástroje měřicí postupy skutečně hlídají. Má-li být metoda hlídána, nemůže v regulačním diagramu hodnota 1 SD činit více, než smysluplnou část např. národních D_max [8,14] resp. celkové povolené chyby. Jakou procentní část D_max může 1 SD určené k zadání do regulačních diagramů činit, je cílem předběžného testu verifikace celkové MP a jejímu správnému stanovení může velmi napomoci rutinní použití 3-signální tabulky prezentované zde jako nová součást řízení IKK.

Tabulka č. 2 uvádí příklad přípustných hodnot pCV_A dle Haeckela a Wosnioka odvozených z empirických variabilit CV_E daných měřených veličin získané v rámci 30denního záznamu IKK. Poskytuje zároveň srovnání s hodnotami reálných a teoretických CV_A dle Jabora a hodnotami CV_A vypočtenými z biologické variability dle Frasera [7]. Hodnoty pCV_A představují vhodný kompromis daný vhodnou volbou referenčních rozmezí (vybrané RI), jež jsou základem výpočtů CV_E.

Malé shrnutí na závěr

3-signální tabulku dle [1] lze s výhodami výše uvedenými použít:

1. ke korektnímu nastavení regulačních diagramů pro IKK
2. v managementu rizik [17, čl. 4.14.6 normy ISO 15189]
3. jako nezávislý indikátor kvality analytické fáze laboratorních procesů měření [17, čl. 4.14.7 normy ISO 15189]
4. k nezávislé analýze vzorků mezilaboratorního porovnání [17, čl. 5.6.3.3 normy ISO 15189]

Seznam zkratek

CV_A analytická variabilita vyjádřená v  % jako variační koeficient

pCV_A přípustný limit CV_A

CV_B biologická variabilita

CV_W intra-individuální variabilita

CV_G inter-individuální variabilita

CV_C kombinovaná variabilita (CV_C= [(CV_W)² + (CV_G)²]^0.5)

CV_E empirická (pozorovaná) variabilita (kombinující CV_C a CV_A)

SD směrodatná odchylka

FPR počet falešně pozitivních chyb (míra specifičnosti)

RL_2,5 dolní, 2,5 %-referenční limit

RL_97,5 horní, 97,5 %-referenční limit

RI referenční interval

EHK externí hodnocení kvality

IKK interní kontrola kvality

Do redakce došlo 15. 1. 2015

Adresa pro korespondenci

MUDr. Jaroslava Ambrožová

Oddělení klinické biochemie Nemocnice Prachatice, a.s.

Nebahovská 1015, 383 01 Prachatice

e-mail: ambrozova@nempt.cz