-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Analýza dat v neurologii XI.
Úvod do statistického usuzování – velikost účinku
Vyšlo v časopise: Cesk Slov Neurol N 2008; 71/104(5): 603-606
Kategorie: Okénko statistika
Ve všech dosavadních dílech seriálu jsme se zabývali tzv. explorační analýzou dat a nabízeli jsme řešení pro popis různých typů výběrových rozdělení náhodných veličin. Vždy šlo o situace, kdy někdo nashromáždil konkrétní data a popisná analýza měla za úkol je popsat, zviditelnit, zpřehlednit. Nyní otevíráme další velkou kapitolu týkající se statistického usuzování, tzv. statistické inference. Zde již nepůjde o prostý popis dat, spíše naopak. Na základě provedeného výběru a předpokladů o rozdělení hodnot se budeme snažit výsledky měření zobecnit na širší skupinu subjektů, případně na celou populaci.
Jistou část této problematiky jsme již probrali, neboť statistické usuzování zahrnuje jednak metodiku odhadování charakteristik výběrového rozdělení a jednak metody tzv. statistického testování. Již dříve vysvětlený bodový a intervalový odhad (např. aritmetického průměru) slouží také k zobecnění hodnot výběrové populace na populaci celkovou, neboť uvádíme interval, v němž se populační hodnota nachází s určitou spolehlivostí. Při statistickém testování pak již přímo provádíme rozhodnutí o platnosti předem dané hypotézy, o rozdělení náhodné proměnné nebo o hodnotě určitého parametru v jedné nebo více populacích.
Je zřejmé, že statistické usuzování je výrazně ambicióznější než sumarizace naměřených dat v konkrétním výběru. Při usuzování bojujeme s variabilitou opakovaných výběrů a samozřejmě se snažíme, aby naše závěry co nejvíce odpovídaly realitě v cílové populaci. Všechny kroky procesu (způsob provedení výběru, velikost vzorku, správnost uplatněných předpokladů o výběrovém rozdělení, použitá statistická metodika) mají na konečný výsledek výrazný vliv. Vždy, když vyslovíme nějaký „statistický soud“ (např. že daná hypotéza pravděpodobně neplatí), musíme ověřit, zda jsme v celém procesu postupovali skutečně správně a zda výsledek usuzování má i reálnou interpretační hodnotu.
Předpokládáme, že čtenáři tohoto seriálu se již s běžnými postupy statistického testování setkali (máme danou hypotézu k ověření -> provedli jsme výběr z populace -> aplikujeme statistický test -> hypotézu prohlásíme za statisticky platnou nebo neplatnou). V závěru hovoříme o „statistické významnosti“ vlivu pokusného zásahu, o významnosti rozdílu dvou a více populací apod. Zcela záměrně ale náš výklad nezačínáme popisem techniky testování a zařazujeme zamyšlení nad smyslem a interpretační hodnotou statistického usuzování. Velmi často se totiž stává, že vlastní provedení výpočtů statistických testů převáží nad úvahami o dosaženém a dosažitelném výsledku. A jelikož statistické usuzování vždy znamená jisté zobecnění z náhodného výběru na celou populaci, je ověření interpretační hodnoty výsledku minimálně stejně významné jako vlastní výpočet. Řeč tedy bude o věcné (klinické) významnosti výsledku, která nemusí vždy odpovídat jeho statistické významnosti.
Vezměme si jako příklad srovnání průměrné výšky lidské postavy mezi dvěma populacemi, například Čechy a Slováky. Srovnáním bodových odhadů průměru na dvou výběrech můžeme dostat numerický rozdíl např. 0,5 cm, který při znalosti rozsahu hodnot jistě nikdo neoznačí za biologicky podstatný nebo významný. Přesto lze i tak malý rozdíl při velkém vzorku vyhodnotit jako statisticky významný a naopak při malém vzorku neprokážeme statistickou významnost ani pro velké rozdíly. Tyto rozpory věcné a statistické významnosti lze v praxi minimalizovat, musíme ale k statistickému testování přistupovat s rozmyslem a plánovitě:
- Kdykoli chystáme měření nebo experimentování za účelem statistického usuzování, měli bychom vědět, proč tak činíme, co chceme prokázat a jaké hodnoty měřených parametrů nebo jejich rozdíly jsou pro nás věcně podstatné. Měření bez této rozvahy nemá žádné opodstatnění a nezachrání ho ani sebedokonalejší statistická analýza. Této části postupu říkáme plánování výběru nebo plánování experimentu („sampling design, experimental design“) a rozhodujeme zde především o způsobu a velikosti výběru nebo o typu uspořádání experimentálních variant. Experimentálními plány pro různé typy hypotéz se budeme zabývat v některém z dalších dílů seriálu.
- Nad naměřenými daty v provedeném výběru vždy zkontrolujeme výběrová rozdělení a posoudíme, jakého jsme dosáhli numerického výsledku. Tato fáze znamená uplatnění prosté statistické sumarizace na všechny získané výběrové soubory. Zahrnuje kontrolu výběrových rozdělení, hledání odlehlých hodnot, odhady statistických charakteristik.
- Přistupujeme k aplikaci statistických testů dle jejich metodiky.
Jak vidno, vlastní statistické výpočty jsou pouze nástrojem, který dokládá spolehlivost dosažených výsledků a umožňuje zobecnění závěrů. Nesmíme je tedy přeceňovat. Platí, že statisticky podložené zobecňování věcně nepodstatných rozdílů nemá žádný smysl a může být dokonce velmi zavádějící. Výsledky úvah popsaných výše v bodě 1 a 2 jsou zásadní, rozhodují o věcném významu výsledku a určují použitelnou statistickou metodologii, neboť ta vždy vychází z ověřených předpokladů o výběrových rozděleních náhodných proměnných. V bodě 2 dále zjišťujeme, jakého efektu jsme u měřené proměnné experimentem dosáhli. Hovoříme o velikosti účinku (ES, Effect Size) experimentálního zásahu nebo intervence.
Absolutní velikost účinku je při srovnání kontrolní a pokusné varianty měřitelná například jako rozdíl odhadů aritmetického průměru (x̄1 - x̄2). Jak ale zjistíme, jaký účinek je věcně podstatný, významný a interpretovatelný? Zde žádné univerzální pravidlo neexistuje, neboť vše závisí na konkrétní situaci, měřeném parametru a cílech výzkumu. V jedné situaci může být za podstatný považován účinek, který v jiném kontextu podstatný není. Nastavení vždy musí provádět člověk znalý věci, který čerpá ze znalosti problému nebo z informací dostupných z literatury. Určením věcně podstatného účinku dáváme zadání i pro plánování velikosti výběru, který musí být nastaven tak, aby minimálně právě takový účinek zachytil a prokázal jako statisticky významný.
Tím, že si stanovíme, jaký účinek je pro nás podstatný, ovšem nijak neovlivňujeme výsledek vlastního měření, a tedy velikost skutečně dosaženého účinku musíme ověřit. K tomu slouží tzv. koeficienty velikosti účinku. Jejich význam je především v tom, že dosažený efekt standardizují a jsou tak využitelné pro srovnávání různých postupů nebo experimentů. Hodnota těchto koeficientů je nezávislá na velikosti výběru. Proto také našly rozsáhlé uplatnění v tzv. metaanalýzách, které sumarizují výsledky dvou nebo více dílčích empirických studií zabývajících se stejným anebo podobným problémem. Pro taková srovnání je nutný odhad velikosti účinků bez ovlivnění velikostí vzorku v konkrétních experimentech. Jako učebnicový příklad takového koeficientu zde uvádíme Cohenův koeficient d používaný pro hodnocení velikosti účinku v testech o dvou výběrových odhadech průměru:
kde x̄1 - x̄2 značí rozdíl aritmetických průměrů naměřených hodnot dvou skupin (pokus, kontrola) a s je společná směrodatná odchylka obou měření. Ze vzorce vyplývá, že hodnota d skutečně standardizuje rozdíly mezi dvěma skupinami pomocí směrodatné odchylky a je nezávislá na rozsahu výběru. Pro jednoduchost budeme uvažovat, že hodnota d nabývá pouze kladných hodnot, tedy že hodnotou x̄1 označíme větší z vypočtených průměrů obou skupin a naopak x̄2 označíme menší z vypočtených průměrů obou skupin.
V literatuře se můžeme setkat s různými formami výpočtu koeficientu d, které se liší v odhadu směrodatné odchylky ve jmenovateli:
- Za určitých okolností je do vzorce za s dosazována hodnota směrodatné odchylky pouze jedné z variant, typicky varianty kontrolní. V literatuře takový koeficient figuruje také pod názvem Glassovo delta. Tento postup je optimální za situace, kdy v experimentu existuje skutečná kontrolní varianta a její variabilita je pro měřenou veličinu reprezentativnější než jiné hodnoty (například pokud je rozptyl hodnot v experimentální variantě změněn v důsledku provedeného zásahu).
- Běžně bývá za s dosazován prostý průměr obou výběrových odhadů směrodatných odchylek. Tento postup lze doporučit, pokud jsou velikosti obou výběrů přibližně stejné a hodnoty s1 a s2 příslušející jednotlivým výběrům se podstatně neliší.
- Další možností je výpočet vážené směrodatné odchylky obou výběrů, kdy je výsledný odhad s (v literatuře: Spooled) vážen velikostí vzorku v jednotlivých výběrech. Výpočet můžeme vyjádřit následovně:
Příklad na obr. 1 dokumentuje právě tento postup výpočtu Cohenova d doplněný 95% intervalem spolehlivosti.
Obr. 1. Výpočet Cohenova koeficientu d a jeho 95% intervalu spolehlivosti [3]. ![Výpočet Cohenova koeficientu d a jeho 95% intervalu spolehlivosti [3].](https://www.prolekare.cz/media/cache/resolve/media_object_image_small/media/image/91afa9b02609751b5295570dd82776a8.jpg)
Rozhodování o velikosti účinku provádíme na základě konvenčně daných limitů pro hodnotu d: při d > 0,8, je efekt velký; pro d v intervalu 0,5–0,8 je efekt střední; efekt pod hodnotou 0,2 označujeme za malý. S rostoucím rozdílem hodnot v čitateli hodnota d logicky roste a dělení směrodatnou odchylkou činí z rozdílu měřítko překrývání srovnávaných výběrových rozdělení: při d = 0 jde o 100% překryv hodnot obou skupin; d rovno 0,8 znamená, že hodnota x̄1 převyšuje 79 % všech hodnot ve skupině 2 atd. (tab. 1).
Tab. 1. Interpretace velikosti účinku na základě Cohenova koeficientu d. 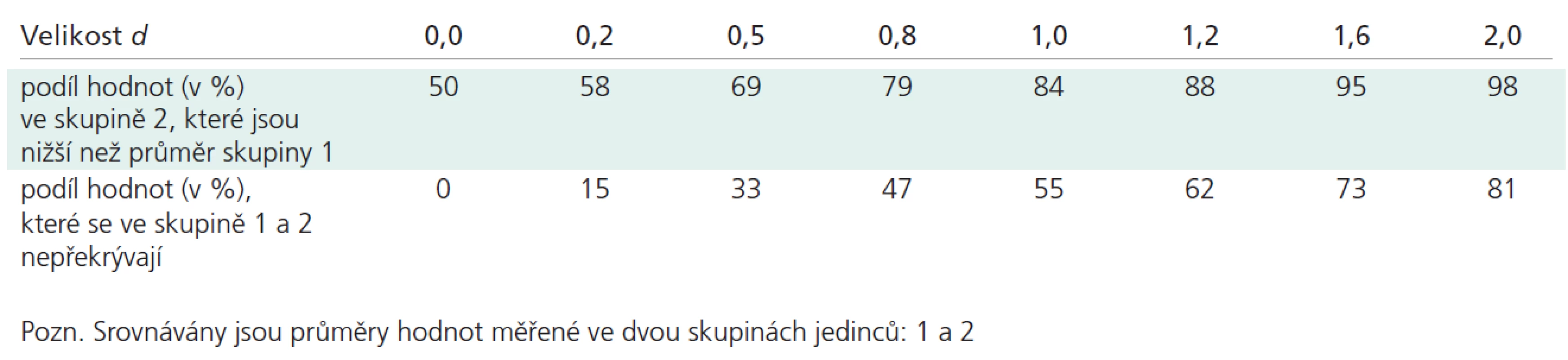
Výpočet Cohenova d je dobrým příkladem univerzálnosti koeficientů účinku. Standardizace pomocí s totiž rozdíl obou průměrů vztahuje k variabilitě (rozsahu) měřené veličiny. Lze tak rovnocenně srovnávat velikost účinku u dvou studií, které měří daný jev pomocí různých ukazatelů, například s rozsahy 0–100 a 0–10. Nutno ovšem připomenout, že všechny zde uvedené výpočty týkající se koeficientu d předpokládají normální rozdělení náhodné veličiny. Koeficientů velikosti účinku existuje samozřejmě více a jejich aplikace se liší podle typu experimentu a rozdělení měřené veličiny. Často jsou takto užívány korelační koeficienty pro hodnocení míry vztahu dvou proměnných. Jiným příkladem může být odvození koeficientu velikosti účinku z analýzy rozptylu. Tzv. Effect Size Correlation i další pokročilé metody budou námětem dalších dílů našeho seriálu.
Velikost účinku lze částečně doložit také pomocí intervalů spolehlivosti prováděných odhadů. Při srovnání dvou výběrových průměrů můžeme například porovnávat intervaly spolehlivosti pro odhad průměru v obou výběrových populacích, nebo bodový odhad průměru v jednom výběru s intervalem spolehlivosti pro výběrový odhad průměru v druhém výběru (experimentální variantě). Takové srovnání nenahrazuje statistický test, ale umožní srovnat skutečné naměřené hodnoty s věcně významným účinkem. Alternativně můžeme provést intervalový odhad přímo pro rozdíl dvou výběrových průměrů a posoudit, zda je klinicky podstatný účinek tímto intervalem pokryt či nikoli. Příklad takového výpočtu je na obr. 2. Je zřejmé, že šířka intervalu spolehlivosti souvisí s velikostí vzorku, takže plně standardizované hodnocení účinku nahradit nemůže. Přesto lze intervaly spolehlivosti doporučit pro prezentaci výsledků, zvláště pokud statistické testy neprokáží významné rozdíly srovnávaných skupin [6]. V takovém případě interval spolehlivosti pro rozdíl průměrů zahrnuje nulu (obr. 2, příklad 2). Z šířky intervalu můžeme usuzovat i na velikost hodnoceného účinku, která je podporována již naměřenými daty.
Obr. 2. Příklad výpočtu intervalu spolehlivosti (IS) pro rozdíl odhadů aritmetického průměru. 
Pevně věříme, že jsme tímto úvodem k statistickému usuzování čtenáře neodradili od dalších dílů. V nich přineseme jasné návody, jaké testy aplikovat v různých situacích. Přesto se nám téma velikosti účinku bude neustále vracet a budeme ho rozebírat především v případech, kdy výsledky vyjdou statisticky nejasně. Kritické posouzení věcného významu výsledků totiž nelze čekat od statistického software, je to úkol experimentátorů a v klinickém výzkumu lékařů. Věříme, že po pročtení tohoto dílu bude čtenář souhlasit s následujícím zlatým pravidlem prezentace vědeckých výsledků: vedle statistické významnosti by měla být vždy doložena i velikost dosaženého účinku a ta doplněná intervalem spolehlivosti. Ačkoli to vypadá jako samozřejmost, zdaleka ne vždy je toto pravidlo dodržováno. I proto zde na závěr dokládáme ukázku výsledkové tabulky (tab. 2), která vyčerpávajícím způsobem dokumentuje význam a spolehlivost naměřených rozdílů mezi dvěma výběrovými průměry.
Tab. 2. Sumarizace naměřených hodnot. 
L. Dušek, T. Pavlík, J. Koptíková
Institut biostatistiky a analýz
Masarykova univerzita, Brno
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
1. Blahuš P. Statistická významnost proti vědecké průkaznosti výsledků výzkumu. Čes Kinantropologie 2000; 4(2): 53–72.
2. Cohen J. Statistical power analysis for the behavioral sciences. 2nd ed. Hillsdale: NJ: Earlbaum 1998.
3. Hedges L. Olkin I. Statistical Methods for Meta‑Analysis. New York: Academic Press 1985.
4. Hoenig JM, Heisey DM. The abuse of power: the pervasive fallacy of power calculations for data analysis. Am Stat 2001; 55 : 19–24.
5. Ives B. Effect size use in studies of learning disabilities. J Learn Disabil 2003; 36(6): 490–504.
6. Johnson DH. The insignificance of statistical significance testing. J Wildl Manage 1999; 63(3): 763–772.
7. Lipsey MW, Wilson DB. The efficacy of psychological, educational, and behavioral treatment: Confirmation from meta‑analysis. Am Psychol 1993; 48(12): 1181–1209.
8. Thompson B. Statistical significance and effect size reporting: portrait of a possible future. Research in the Schools 1995; 5(2): 33–38.
Štítky
Dětská neurologie Neurochirurgie Neurologie
Článek vyšel v časopiseČeská a slovenská neurologie a neurochirurgie
Nejčtenější tento týden
2008 Číslo 5- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Magnosolv a jeho využití v neurologii
- Moje zkušenosti s Magnosolvem podávaným pacientům jako profylaxe migrény a u pacientů s diagnostikovanou spazmofilní tetanií i při normomagnezémii - MUDr. Dana Pecharová, neurolog
- Zolpidem může mít širší spektrum účinků, než jsme se doposud domnívali, a mnohdy i překvapivé
- Nejčastější nežádoucí účinky venlafaxinu během terapie odeznívají
-
Všechny články tohoto čísla
- Neurologické poruchy v rámci kritického stavu
- Matrixové metaloproteinázy v patogenezi roztroušené sklerózy
- Současná diagnostika a léčba oligodendrogliomů
- Význam monitorování mozkové aktivity pomocí integrované amplitudy EEG aktivity u novorozenců s časným asfyktickým syndromem
- Pravo/levorukost a preference druhostranné dolní končetiny. Testování laterality a mozečkové dominance
- Traumatické poranění mozku a zlomeniny obličejového skeletu
- Radiochirurgická léčba kraniofaryngeomů v kombinaci s ostatními stereotaktickými metodami
- Kombinované poranění atlasu a čepovce
- Míšní metastáza adenokarcinomu – kazuistika
- Neurosarkoidóza: zriedkavý prípad sarkoidózy krčnej miechy – kazuistika
-
Komentář k práci Mraček J. Intradurální výhřez bederní meziobratlové ploténky manifestující se syndromem kaudy – kazuistika
Věčné téma: výhřez meziobratlové ploténky, tentokrát intradurální - Intradurální výhřez bederní meziobratlové ploténky manifestující se syndromem kaudy – kazuistika
- Mozková gliomatóza – kazuistika
- Webové okénko
-
Analýza dat v neurologii XI.
Úvod do statistického usuzování – velikost účinku - Recenze
- Ne uromuskulární kongres v Brně
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Intradurální výhřez bederní meziobratlové ploténky manifestující se syndromem kaudy – kazuistika
- Současná diagnostika a léčba oligodendrogliomů
- Neurologické poruchy v rámci kritického stavu
- Neurosarkoidóza: zriedkavý prípad sarkoidózy krčnej miechy – kazuistika
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání





