-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Analýza dat v neurologii
IX. Poissonovo rozdělení
Autoři: L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů: Masarykova univerzita, Brno ; Institut biostatistiky a analýz
Vyšlo v časopise: Cesk Slov Neurol N 2008; 71/104(3): 359-362
Kategorie: Okénko statistika
V minulém díle našeho seriálu jsme se zabývali binomickým rozdělením sloužícím pro popis četnosti výskytu náhodného jevu v n nezávislých pokusech. Sledovaný jev má přitom stále stejnou pravděpodobnost (v modelu ji vyjadřuje parametr π, v odhadu p), že nastane. Dále předpokládáme konečný počet opakování experimentu (n), ve kterých sledovaný jev může nastat s četností 0 až n. Poissonovo rozdělení je velmi podobné binomickému, neboť rovněž sleduje výskyt jevu v konečném počtu experimentů nebo měření. Binomické rozdělení přechází v Poissonovo při rostoucím n (n → ∞) a klesajícím p (p → 0). Tato aproximace na Poissonovo rozdělení je funkční již při n > 30 a p < 0,1. Proto se o Poissonově rozdělení říká, že modeluje výskyt málo četných nebo vzácných jevů. To ale není zcela přesné, neboť Poissonovo rozdělení lze použít i pro modelování výskytu relativně četných jevů, samozřejmě jsou-li naplněny předpoklady pro jeho aplikaci. U jevů vzácných ale představuje nenahraditelný nástroj.
Strohá definice říká, že náhodná veličina má Poissonovo rozdělení, pokud vyjadřuje počet výskytů málo pravděpodobných jevů v určitém časovém nebo objemovém intervalu. Při praktické výuce lékařů nebo biologů jsme zjistili, že v této definici trochu zaniká přidaná hodnota celého modelu, a proto si zde dovolíme jeho účel poněkud více popsat. U binomického rozdělení (viz VIII. díl našeho seriálu) realizujeme n nezávislých pokusů, např. hodů mincí. Základní koncept počítá s tím, že u každého jednotlivého hodu umíme posoudit, zda nastal sledovaný jev. Je lhostejné, zda hodů je 10 nebo 10 milionů, princip zůstává stejný, roste pouze pracnost měření. Začneme-li takto sledovat vzácný jev, opět se princip nemění, jen roste požadavek na nutný počet opakování experimentu, abychom daný jev vůbec uviděli. Nicméně nadále u každé jednotlivé „experimentální jednotky“ (hod mincí, měřený objekt, situace) umíme posoudit „individuálně“, zda jev nastal nebo ne.
Kvalitativně zcela nová situace nastane ve chvíli, kdy se skutečně naplní n → ∞ a počet jednotlivých experimentů začne být individuálně neměřitelný. Jedinou možností, jak v takové situaci uspět při sledování výskytu jevu, je práce s jinak definovanými širšími experimentálními jednotkami, tedy např. s časovými intervaly, plochou, objemovými intervaly nebo jinak účelově nastavenými celky, ve kterých provádíme sledování (výrobní směna, příjem v nemocnici, sezona…). V takové situaci binomické rozdělení již použít vůbec nelze. Poissonovo rozdělení je ale právě na tyto experimenty nastaveno a sleduje výskyt jevu v časových a prostorových experimentálních jednotkách. Základním cílem je zjistit průměrný výskyt jevu na jednu experimentální jednotku. Jako příklady uvádíme (obr. 1):
- mutace bakterií měřené klasickým výsevem kolonií na Petriho misku (sledován je průměrný výskyt na 1 misku)
- počet krvinek v poli mikroskopu, kde experimentální jednotkou je buď definovaná plocha políčka, nebo objem hodnocené jamky
- počet žížal vyskytujících se na určité ploše pole (měřeno opakovaným průzkumem vybrané plochy, např. 1 m2)
- počet pooperačních komplikací během určitého časového intervalu po výkonu
- počet částic, které vyzáří zářič za danouasovou jednotku.
Obr. 1. Příklady praktického využití Poissonova rozdělení. 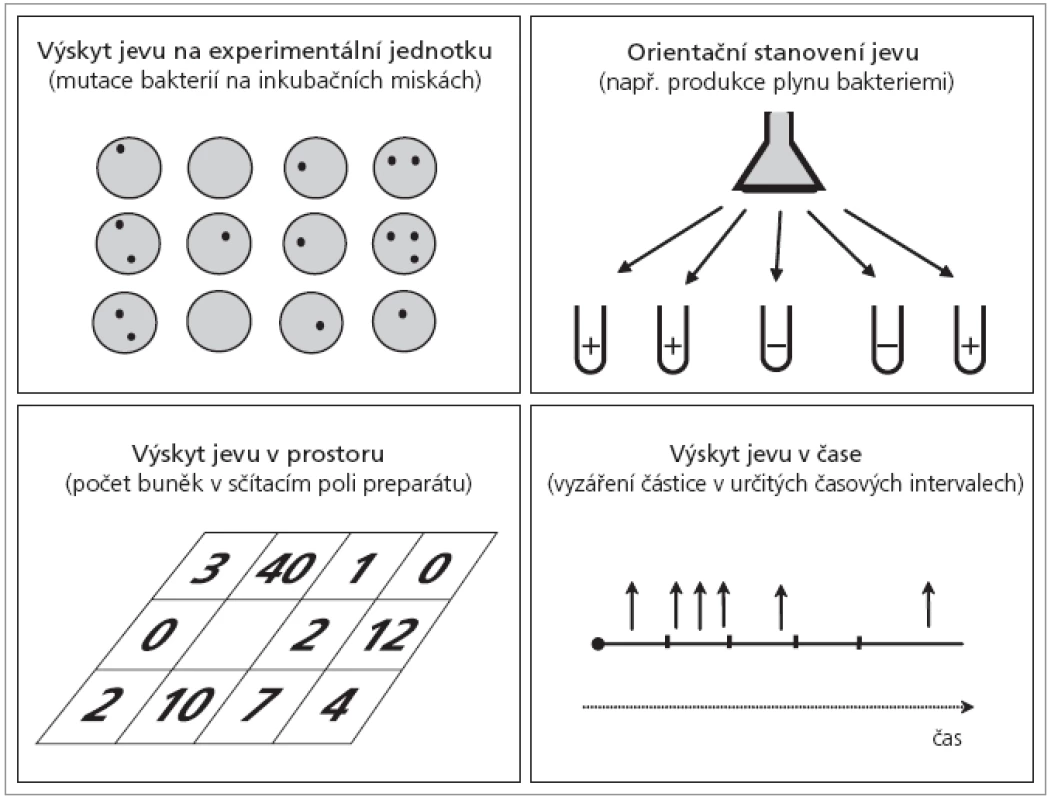
Všechny výše uvedené příklady reprezentují stejnou experimentální situaci a postup:
- Definujeme experimentální jednotku (časový úsek, plocha), kterou následně opakovaně používáme k měření.
- Za stále stejných podmínek sledujeme výskyt daného jevu v definovaných experimentálních jednotkách (tedy již ne sledování jednotlivých hodů mincí nebo jednotlivých bakterií, sledujeme větší interval nebo časový úsek).
- Ze zaznamenaných počtů jevů v experimentálních jednotkách počítáme střední výskyt jevu na 1 experimentální jednotku. Jelikož ta má stanovenou měřitelnou velikost, lze střední výskyt jevu přepočítat na větší celky nebo jinak zobecnit.
Poissonovo rozdělení slouží k odhadu středního výskytu jevu a následně k modelování pravděpodobnosti, že jev se vyskytne v nějak určeném počtu (např. právě jednou, více než 5krát apod). Tak jako i jiná rozdělení pravděpodobnosti, má Poissonovo rozdělení nutné předpoklady pro svou aplikaci:
- výskyt jevu je zcela náhodný (tedy náhodný v čase nebo prostoru podle typu situace)
- výskyt jevu v konkrétní experimentální jednotce nijak nezávisí na tom, co se stalo v jiných jednotkách
- není možné, aby 2 nebo více jevů nastaly současně, přesně ve stejném místě prostoru nebo ve stejném časovém okamžiku
- pro každý dílčí časový okamžik, prostorovou jednotku nebo jinak definovanou jednotku je pravděpodobnost výskytu jevu stejná.
Poissonovo rozdělení je tedy modelem pro výskyt jevů, které se náhodně vyskytují v čase nebo prostoru s neměnnou pravděpodobností. Počítáme-li např. mutované kolonie na Petriho misce, předpokládáme, že pravděpodobnost mutace každé jednotlivé bakterie v průběhu experimentu je stejná a výskyt mutací je zcela náhodný. Obr. 2 ukazuje alternativy k náhodnému výskytu, tedy výskyt rovnoměrný nebo shlukový, což jsou situace, na které musí být použit jiný stochastický model.
Obr. 2. Poissonovo rozdělení je model sledující náhodný výskyt jevu. 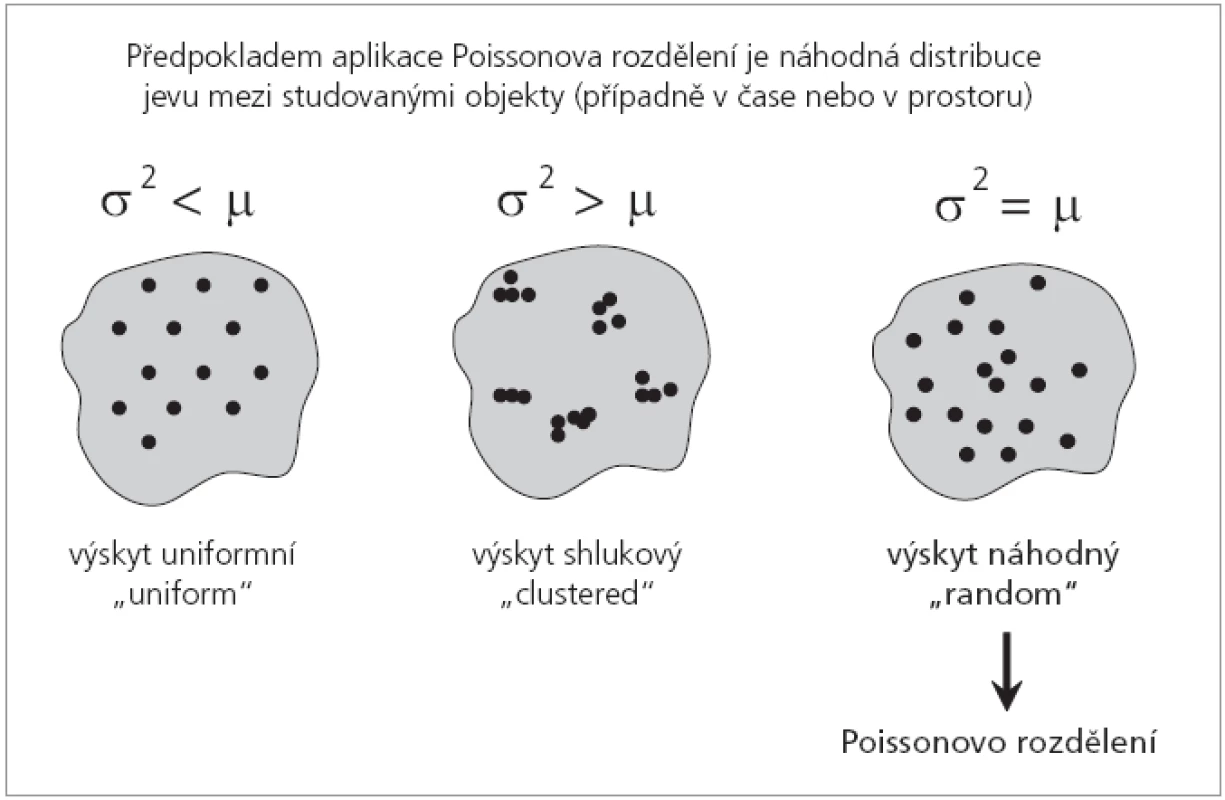
Jak již bylo řečeno, cílem hodnocení je odhad střední hodnoty počtu jevů (událostí) na danou jednotku. V Poissonově rozdělení střední hodnotu počtu jevů X označujeme jako λ. Parametr λ je jediným parametrem pravděpodobnostní funkce P (X), která je popsána a graficky znázorněna na obr. 3. Je zajímavé, že proměnná X s Poissonovým rozdělením má střední hodnotu rovnu rozptylu:
E (X) = Var (X) = μ = σ2 = λ (obr. 2).
Obr. 3. Poissonovo rozdělení jako model. 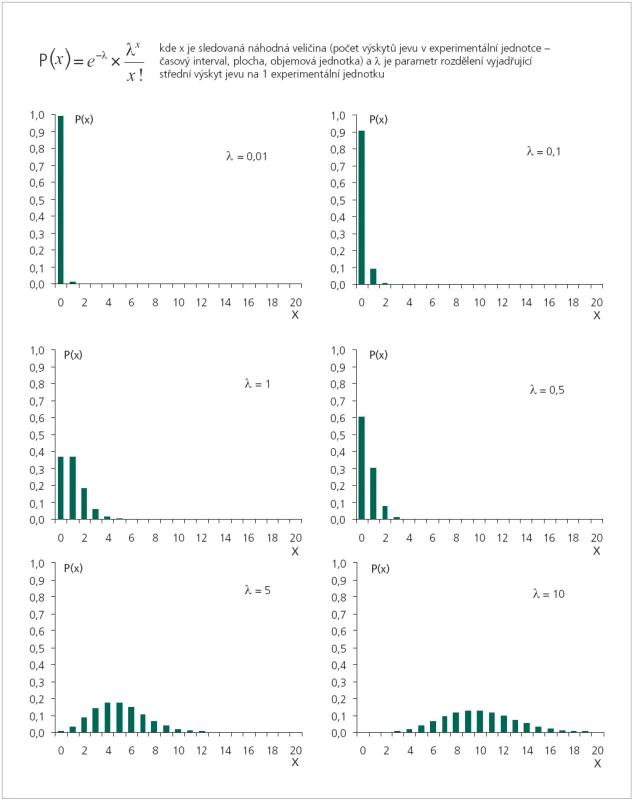
Obr. 3 jasně dokládá, že čím větší je λ, tím více se tvar Poissonova rozdělení blíží rozdělení normálnímu. Tímto potvrzujeme, že Poissonovo rozdělení může být využito i pro modelování výskytu častých jevů. Pokud k Poissonovu rozdělení vede aproximace binomického rozdělení při n → ∞ a p → 0, pak hodnota λ = np. Z toho je opět patrný číselný význam parametru λ, který vyjadřuje střední počet jevů v dané experimentální situaci.
Hlavní pragmatickou hodnotu Poissonova rozložení asi nejlépe přiblíží konkrétní příklad. Aplikujme Poissonovo rozdělení na sledování určité komplikace u pacienta v čase (náhodná veličina X) s tím, že základním časovým intervalem pro měření je 1 h. Během opakovaných měření v tomto intervalu jsme zjistili, že střední výskyt sledované komplikace je λ = 1. Jsou-li splněny všechny předpoklady Poissonova rozdělení, můžeme využít jeho pravděpodobnostní funkci k modelovým výpočtům, které umožní odhadnout pravděpodobnost různých potenciálně rizikových situací. Uveďme jako příklad 2 takové otázky, přičemž pro výpočet využijeme vztah uvedený na obr. 3:
1. Jaká je pravděpodobnost, že veličina X nabude hodnoty x = 1?
P (x = 1) = (λ1/1!)/eλ = 0,3679
2. Jaká je pravděpodobnost, že veličina X nabude hodnoty alespoň 2, tedy x ≥ 2?
Pravděpodobnost P (x ≥ 2) je rovna součtu pravděpodobností
P (x = 2) + P (x = 3) + P (x = 4) +…,
lépe ji ale spočítáme jako
P (x ≥ 2) = 1 – P (x = 0) – P (x =1):
P (x = 0) = (λ0/0!)/eλ = 0,3679
P (x = 1) = 0,3679 (viz bod 1)potom
P (x ≥ 2) = 1 – 0,3679 – 0,3679 = 0,2642
Příklad ukazuje, že pro
λ = 1 je P (x = 0) = P (x = 1).
S parametrem λ samozřejmě není nutné pracovat pouze jako s bodovým odhadem. Bodový odhad můžeme doplnit i intervalem spolehlivosti tak, jak jsme jej dříve dokumentovali například pro odhad aritmetického průměru. Příklad takového výpočtu intervalu spolehlivosti ukazuje obr. 4.
Obr. 4. Výpocet intervalu spolehlivosti pro parametr λ Poissonova rozdělení. 
Závěrečná poznámka musí patřit samotnému názvu Poissonova rozdělení, neboť ten není tak „anonymní“ jako u rozdělení binomického. Rozdělení je pojmenováno po významném francouzském matematikovi a fyzikovi Poissonovi. Siméon-Denis Poisson žil v letech 1781 až 1840 a za svůj život toho stihnul opravdu hodně. Byl profesorem na École Polytechnique v Paříži, členem Francouzské akademie věd a Petrohradské akademie věd. Zabýval se matematickou analýzou, řešením diferenciálních rovnic i teorií pravděpodobnosti. Zavedl pojem „zákon velkých čísel“. Kromě toho řešil pohybové rovnice v mechanice, významně přispěl k poznání magnetických a elektrických jevů a zabýval se teorií pružnosti a tepla. Nezbývá než konstatovat, že Poissonovo rozdělení má více než důstojný původ svého názvu.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Štítky
Dětská neurologie Neurochirurgie Neurologie
Článek Asociace vybraných rizikových faktorů s tíží aterosklerotického postižení v karotické bifurkaciČlánek Retrospektivní analýza nálezů zrakových evokovaných potenciálů při akutním zánětu zrakového nervuČlánek Tau-protein, fosforylovaný tau-protein a beta-amyloid42 v likvoru u demencí a roztroušené sklerózyČlánek Migréna v těhotenstvíČlánek Sporadický „guamský parkinsonský komplex“ nebo koincidence více neurodegenerativních onmocnění?Článek Webové okénkoČlánek Gerhard Waberžinek
Článek vyšel v časopiseČeská a slovenská neurologie a neurochirurgie
Nejčtenější tento týden
2008 Číslo 3- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Moje zkušenosti s Magnosolvem podávaným pacientům jako profylaxe migrény a u pacientů s diagnostikovanou spazmofilní tetanií i při normomagnezémii - MUDr. Dana Pecharová, neurolog
- Magnosolv a jeho využití v neurologii
- Nejčastější nežádoucí účinky venlafaxinu během terapie odeznívají
-
Všechny články tohoto čísla
- Degenerace krční meziobratlové ploténky – indikace a možnosti chirurgické léčby
- Depersonalizace a derealizace – současné nálezy
- Sexuální dysfunkce u žen s epilepsií a jejich příčiny
- Pohybové aktivity pacientů trpících dědičnou polyneuropatií
- Asociace vybraných rizikových faktorů s tíží aterosklerotického postižení v karotické bifurkaci
- Funkce pravé komory srdeční a výskyt plicní hypertenze u pacientů se syndromem obstrukční spánkové apnoe
- Přínos vyšetření čichu v časné diagnostice demencí neurodegenerativní etiologie
- Analýza pulzové vlny v objektivizaci bolesti – předběžné sdělení
- Kvalita života u pacientů po subarchnoidálním krvácení – roční katamnéza
- Retrospektivní analýza nálezů zrakových evokovaných potenciálů při akutním zánětu zrakového nervu
- Laboratorní ukazatele neurodegenerace v likvoru a míra motorického postižení u Parkinsonovy nemoci: korelační studie
- Tau-protein, fosforylovaný tau-protein a beta-amyloid42 v likvoru u demencí a roztroušené sklerózy
- Migréna v těhotenství
- Sporadický „guamský parkinsonský komplex“ nebo koincidence více neurodegenerativních onmocnění?
- Použití DTI traktografie v neuronavigaci při operacích mozkových nádorů: kazuistiky
- Webové okénko
-
Analýza dat v neurologii
IX. Poissonovo rozdělení - Gerhard Waberžinek
- Management ischemické cévní mozkové příhody a tranzitorní ischemické ataky – doporučení European Stroke Organisation (ESO) 2008 – zestručněná česká verze
- Doporučený postup sekundární prevence recidivy po akutní cévní mozkové příhodě: mozkovém infarktu/tranzitorní ischemické atace a hemoragické cévní mozkové příhodě
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Depersonalizace a derealizace – současné nálezy
- Degenerace krční meziobratlové ploténky – indikace a možnosti chirurgické léčby
- Migréna v těhotenství
- Pohybové aktivity pacientů trpících dědičnou polyneuropatií
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



