-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
ROC analýza a využití analýzy nákladů a přínosů k určení optimálního dělícího bodu
Autoři: J. Vránová 1; J. Horák 2; K. Krátká 2; M. Hendrichová 2; K. Kovaříková 2
Působiště autorů: Univerzita Karlova v Praze, 3. lékařská fakulta, Ústav lékařské biofyziky a lékařské informatiky 1; Univerzita Karlova v Praze, 3. lékařská fakulta, I. interní klinika 2
Vyšlo v časopise: Čas. Lék. čes. 2009; 148: 410-415
Kategorie: Přehledový článek
Souhrn
Ve své práci jsme předložili přehled o ROC (receiver operating characteristic) analýze a jejím použití v medicíně. Článek uvádí krátký přehled teorie i způsob, jak lze ROC křivku vytvořit, a dále zdůrazňuje význam analýzy nákladů a přínosů (Cost-Benefit Analysis) při volbě optimálního dělícího bodu (prahu). Použití ROC analýzy jsme ukázali na několika příkladech v části „Analýza nákladů a přínosů“. Na těchto příkladech vidíme, že pro určení optimálního dělícího bodu má rozhodující význam prevalence onemocnění, závažnost onemocnění, rizika a nežádoucí účinky léčby nebo diagnostického testu, celkové náklady na léčbu pravdivě i falešně pozitivních pacientů i riziko nedostatečné nebo žádné léčby u falešně negativních.
Klíčová slova:
ROC analýza, ROC křivka, senzitivita, specificita, pozitivní prediktivní hodnota, negativní prediktivní hodnota, prevalence, analýza nákladů a přínosů, plocha pod křivkou, screeningový test, optimální dělící bod.Úvod
ROC křivka (receiver operating characteristic curve – graf prahové operační charakteristiky) byla vyvinuta americkými vědci a poprvé použita během 2. světové války pro přesnější detekci nepřátelských objektů. Je součásti teorie detekce signálů (1, 2). Dnes nachází široké uplatnění především v oblasti medicíny při lékařském rozhodování, např. v epidemiologii, radiologii, psychologii (3) apod. V posledních letech se ROC analýza stala důležitým nástrojem v oblasti strojového učení pro vyhodnocování a porovnávání kvality algoritmů neuronových sítí a metody data mining (4, 5).
V oblasti medicíny se užívá především pro hodnocení kvality a síly diskriminace diagnostických či screeningových testů, regresních a diskriminačních modelů, při zavádění nových diagnostických přístrojů, nových léků a nových způsobů léčby do medicínské praxe a také při porovnávání více diagnostických metod za účelem vybrat tu nejlepší, při porovnávání různých analytických modelů apod. Její neoddělitelnou součásti se dnes stala analýza nákladů a přínosů (Cost-Benefit Analysis).
ROC analýza – definice veličin
Tradiční ROC analýza se obvykle používá pro případ dvou tříd, protože se jednoduše definuje a interpretuje. Umožňuje vyhodnocení a grafické znázornění chování klasifikátorů při klasifikaci právě do těchto dvou tříd.
Předpokládejme, že máme skupinu vyšetřovaných osob a na základě diagnostického (screeningového) testu máme rozhodnout, kteří jedinci jsou zdraví a kteří trpí sledovaným onemocněním. Po definici vhodného prahového (dělícího) bodu, který nám právě rozdělí náš vyšetřovaný soubor na zdravé jedince a pacienty, a s ohledem na skutečnost, že všechny testy vykazují jistou nejednoznačnost, dostaneme po naměření hodnot čtyři množiny osob:
- True positive (TP) – pacienti s nemocí, které test označil správně jako nemocné.
- True negative (TN) – zdraví jedinci s negativní hodnotou testu.
- False positive (FP) – zdraví jedinci s pozitivní hodnotou testu.
- False negative (FN) – nemocní pacienti, které test nezachytil (jsou nesprávně klasifikováni jako zdraví).
Přehledné znázornění těchto množin vidíme v tabulce 1, kterou též nazýváme jako tabulku záměn (6). V oblasti medicíny, v regresní analýze se tato tabulka spíše označuje jako klasifikační, protože nám zobrazuje počet správně a nesprávně klasifikovaných případů.
Tab. 1. Tabulka záměn (klasifikační tabulka), se skutečnými počty případů – pravdivě pozitivních, falešně pozitivních, pravdivě negativních a falešně negativních 
TP – pravdivě pozitivní, FP –falešně pozitivní, FN –falešně negativní, TN – pravdivě negativní Z předchozích hodnot můžeme nadefinovat základní veličiny ROC analýzy:
Senzitivitu, též také TPR (true positive rate – pravdivě pozitivní poměr), která je definována jako poměr mezi pacienty, kteří byli pomocí testu správně klasifikováni, a všemi pacienty, kteří dané onemocnění skutečně mají.
Specificitu, nebo také TNR (true negative rate – pravdivě negativní poměr), kterou definujeme jako poměr mezi zdravými jedinci, které test správně vyloučil, a všemi zdravými jedinci.
Dále definujeme FPR (false positive rate – falešně pozitivní poměr) a FNR (false negative rate – falešně negativní poměr) následujícími vztahy:
Je potřeba si všimnout, že FPR = 1 – TNR a FNR = 1 – TPR.
Dalšími důležitými veličinami ROC analýzy jsou prediktivní hodnoty diagnostického testu, a to:
PPV (positive predictive value) – pozitivní prediktivní hodnota testu, která nám určuje, jaká je pravděpodobnost, že pacient je nemocný, když je test pozitivní. Definujeme ji jako poměr pravdivě pozitivních testů ke všem pozitivním testům.
NPV (negative predictive value) – negativní prediktivní hodnota testu, která nám definuje přesnost negativní predikce. Je to poměr pravdivě negativních testů a všech negativních testů.
Senzitivita a specificita jsou charakteristiky samotného diagnostického testu, naproti tomu prediktivní hodnoty jsou velmi závislé na prevalenci onemocnění. Pomocí prevalence můžeme tyto hodnoty vyjádřit následovně:
a
kde P(D+) je prevalence onemocnění.
Když známe výsledek diagnostického testu, můžeme spočítat aposteriorní (potestovou) pravděpodobnost výskytu onemocnění. Tyto aposteriorní pravděpodobnosti jsou právě dány hodnotami PPV a NPV a jsou předmětem prvořadého zájmu pro kliniky. Dobrý diagnostický či screeningový test je takový, jehož výsledek zvyšuje kvalitu předpovědi o výskytu onemocnění oproti předpovědi založené pouze na prevalenci onemocnění (7).
Další veličinou, kterou v ROC analýze definujeme je přesnost screeningového testu, kterou definujeme jako podíl součtu všech jedinců správně klasifikovaných (TP + TN) a všech osob podrobených diagnostickému testu (n).
Konstrukce ROC křivky
Pokračujme dále v našem příkladu se skupinou vyšetřovaných osob a navíc předpokládejme, že náš diagnostický test při své vysoké hodnotě signalizuje větší pravděpodobnost výskytu onemocnění než při hodnotě nízké. Naměřené hodnoty si nejprve seřadíme podle velikosti (v našem případě od největší po nejmenší). U každé naměřené hodnoty si poznamenáme, zda pacient s touto hodnotou testu je zdravý nebo nemocný a dále si pro každou hodnotu spočteme senzitivitu a hodnotu FPR = 1 – specificita. ROC křivku sestrojíme právě z těchto dvou hodnot, a to na osu x vynášíme postupně hodnoty FPR (nebo 1 – specificita) a na osu y hodnoty TPR (nebo senzitivity). Příklad grafu ROC křivky spolu s optimálním, přísným a nedbalým prahem vidíme na obrázku 1. Teď již můžeme spočítat poslední důležitou veličinu ROC analýzy, a tou je plocha pod křivkou, označovaná také jako AUROC nebo jenom AUC (area under the ROC curve).
Obr. 1. Graf ROC křivky spolu s oblastí přísného, optimálního a nedbalého prahu 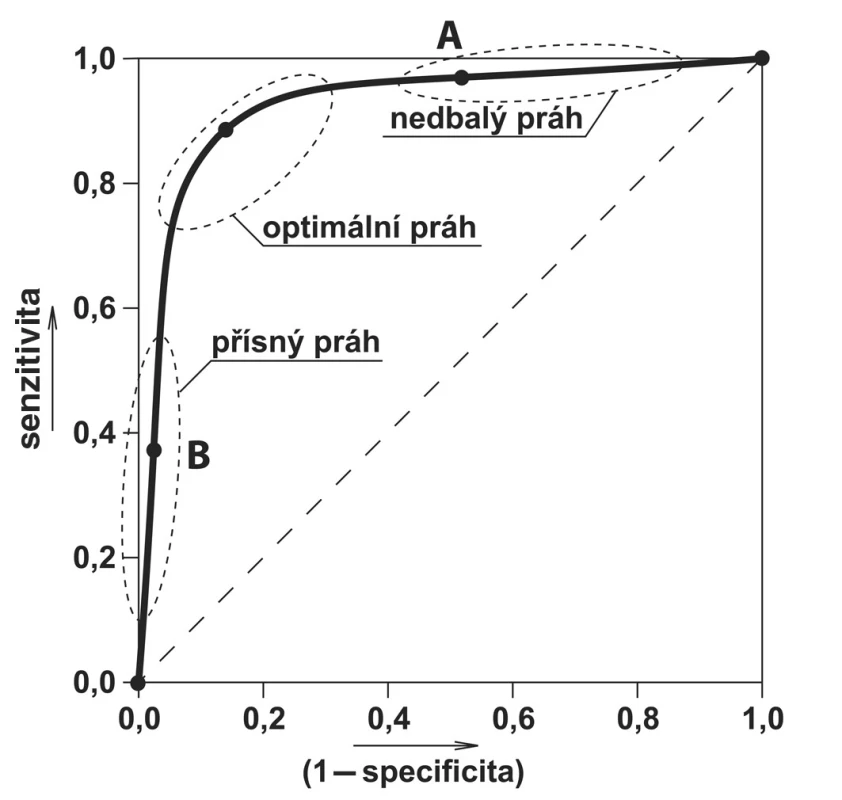
Plocha pod křivkou
Plocha pod křivkou je neparametrická veličina, netrpí zkreslením, ke kterému dochází při nevyváženém zastoupení jednotlivých tříd v populaci, neexistují problémy s tzv. „nenormalitou“ rozložení. Navíc vykazuje velmi velkou podobnost s Wilcoxonovým a Mannovým-Whitneyho U-testem.
Plocha pod křivkou nabývá libovolných hodnot od 0 (resp. 0,5) do hodnoty 1 a právě její velikost definuje diskriminační kvalitu diagnostického testu nebo regresního modelu. Čím více se blíží 1 (100 %), tím je test kvalitnější. Hodnocení kvality testu podle velikosti plochy pod křivkou definujeme podle Tapea (8) následující stupnicí:
- 0,50–0,60 … selhání (FAIL),
- 0,60–0,70 … slabá (POOR),
- 0,70–0,80 … slušná (FAIR),
- 0,80–0,90 … dobrá (GOOD),
- 0,90–1,00 … výtečná (EXCELLENT),
přičemž, pokud je velikost plochy AUC = 0,50, má náš diagnostický test asi stejnou hodnotu, jako bychom si při příchodu pacienta do ambulance hodili mincí a na základě toho rozhodli, zda je nemocen nebo zdráv.
Určení optimálního dělícího bodu
Nejdůležitějším úkolem ROC analýzy je nadefinovat optimální polohu dělícího bodu. Na obrázcích 2 až 4 postupně vidíme, že při libovolném posunutí prahové hodnoty se nám mění všechny základní charakteristiky ROC analýzy, tj. TP, TN, FP, FN a tedy i senzitivita, specificita, PPV a NPV.
Obr. 2. Poloha nízkých hodnot screeningového testu 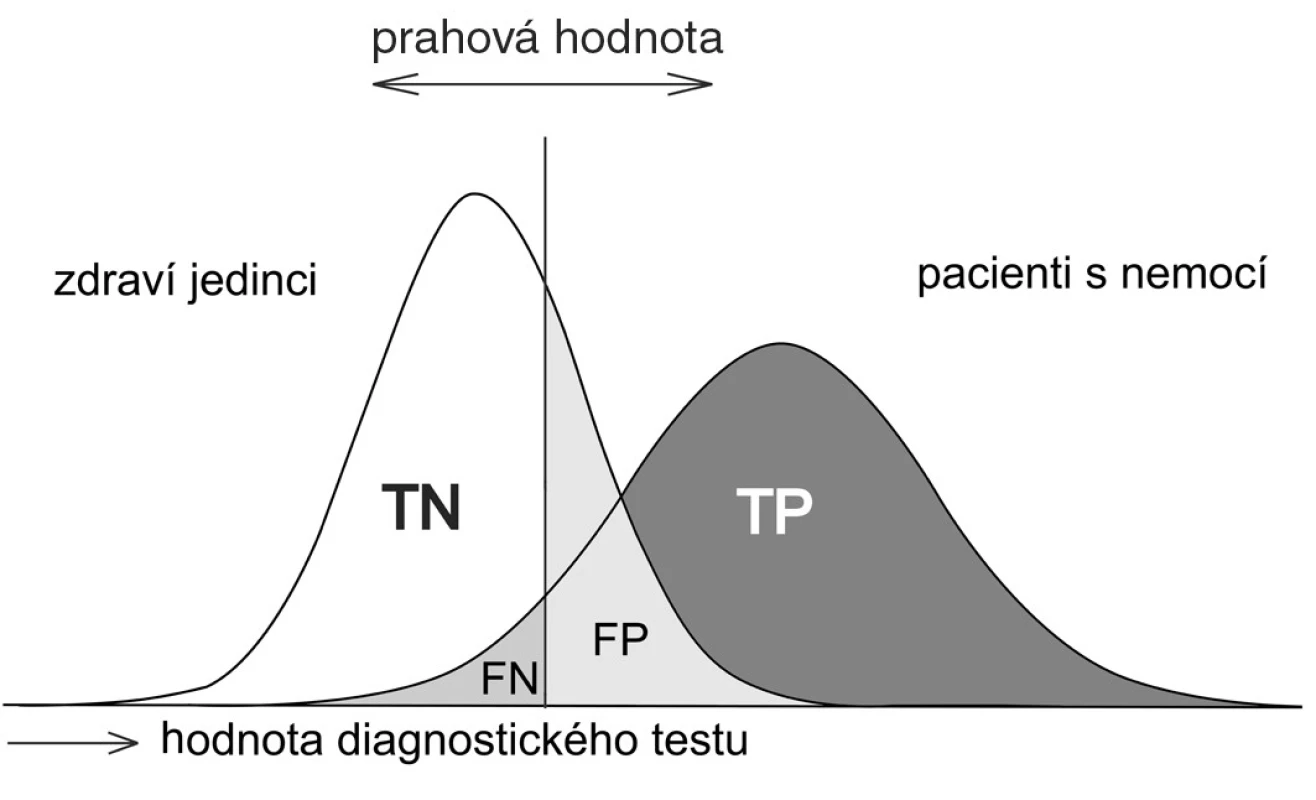
Obr. 3. Posun dělící linie (prahové hodnoty) screeningového testu k vyšším hodnotám 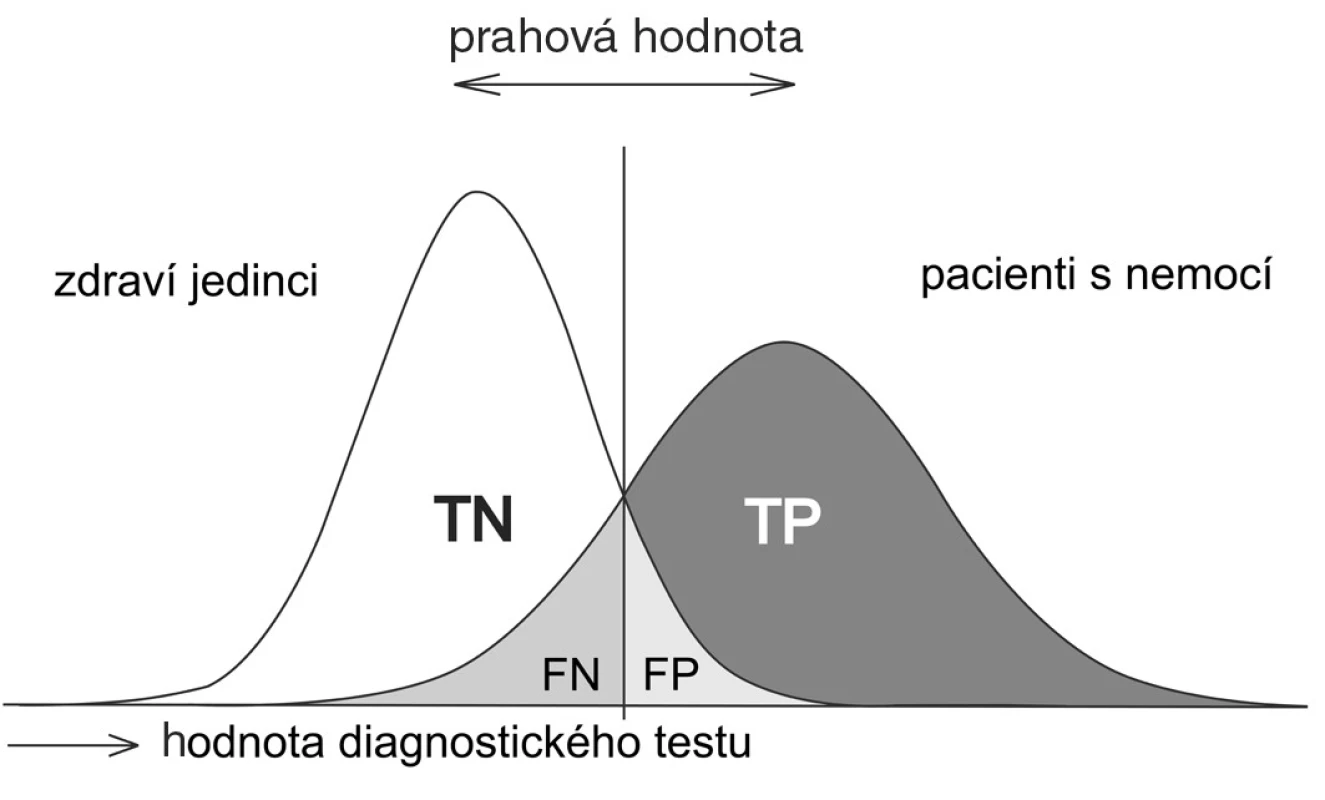
Obr. 4. Posun dělící linie (prahové hodnoty) screeningového testu k vysokým hodnotám Při postupném posunu od nízkých hodnot testu k vyšším hodnotám dochází k poklesu počtu falešně pozitivních případů, avšak za současného poklesu pravdivě pozitivních. 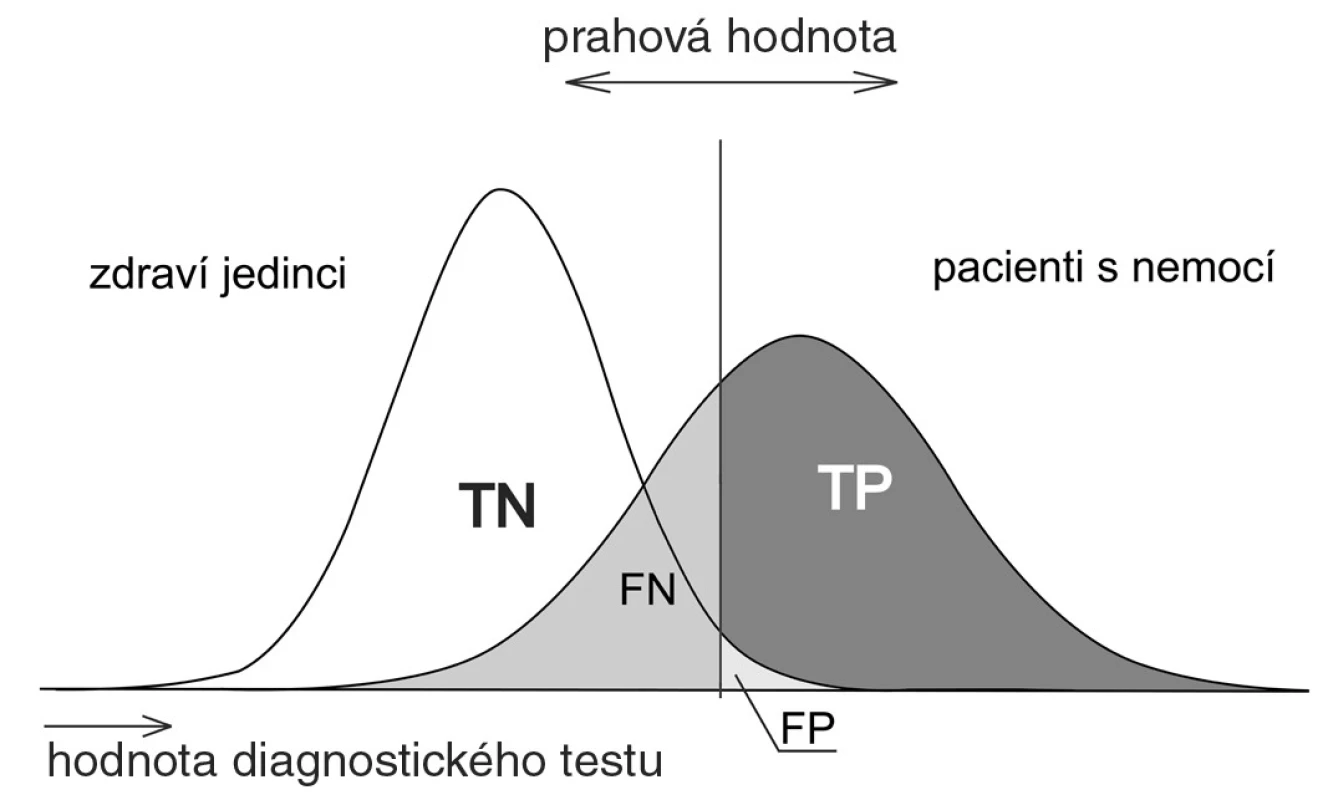
Posunutí prahového bodu zleva doprava (posunutí dělicí čáry postupně na obrázcích 2, 3 a 4) odpovídá pohybu prahového bodu po ROC křivce, také zleva doprava (tento pohyb vidíme na obrázku 1). Prahový bod se pohybuje od „nejpřísnějšího“ prahu (bod [0, 0]), postupně přes oblast „přísného“, „optimálního“ a „nedbalého“ prahu až do bodu [1, 1], který nazýváme „nejvíce nedbalým“. V oblasti „přísného“ prahu jsou kritéria pro přijetí pozitivního testu nastavena velmi přísně, tj. málokterého pacienta klasifikujeme jako nemocného. Tato skutečnost minimalizuje počet falešně pozitivních, avšak za cenu ztráty citlivosti (senzitivity), tedy velká část pravdivě pozitivních – čili skutečně nemocných – nebude správně diagnostikována. Naopak v oblasti „nedbalého“ prahu jsou kritéria nastavena tak, že téměř všichni vyšetřovaní jsou zachyceni jako nemocní. Počet pravdivě pozitivních se sice blíží 100 %, důsledkem je však velký počet falešně pozitivních. Mezi těmito oblastmi leží oblast optimálního prahového bodu – oblast, která je nejblíže hornímu levému rohu a ve které jsou senzitivita i specificita maximalizovány. Kam a za jakých podmínek umístíme dělící bod, si ukážeme na příkladech v části „Analýza nákladů a přínosů“.
V mnoha vědeckých publikacích se ještě i dnes setkáváme s určením polohy dělícího bodu bez jakéhokoliv teoretického nebo vědeckého vysvětlení, bez toho, aby byly brány v úvahu riziko nebo prospěch přebytečné léčby nebo naopak nedostatečné léčby bez ohledu na prevalenci onemocnění apod. (9). Sem patří případy jako:
- Je vybrán libovolný bod bez jakéhokoliv vysvětlení.
- Bod na ROC křivce je vybrán tak, aby byl co nejblíže levému hornímu rohu (senzitivita i specificita se blíží 100 %).
- Požadovaná hodnota senzitivity je stanovena předem, odpovídající specificita je určena z křivky.
- Součet senzitivity a specificity je maximalizován.
- Je vybrán bod, ve kterém se senzitivita rovná specificitě.
Pro skutečně odpovědný přístup pro stanovení optimálního dělícího bodu je nutné do ROC analýzy zabudovat pravidla analýzy nákladů a přínosů.
Analýza nákladů a přínosů
Podle analýzy nákladů a přínosů to, kam umístíme náš prahový bod, ovlivňují následující kritéria (10):
- finanční náklady – přímé i nepřímé na léčbu nemoci (přítomné i nepřítomné) a to i v případě, když dané onemocnění neléčíme,
- náklady na případný další výzkum,
- diskomfort pacienta,
- mortalita spojená s léčením nebo neléčením pacienta,
- prevalence onemocnění.
Optimální dělící bod zvolíme tak, abychom optimalizovali užitek diagnostické metody, s ohledem na výše uvedená kritéria (10).
Celkové náklady na léčbu si můžeme vyjádřit následující rovnicí (10):
kde C jsou režijní náklady na provedení samotného testu.
Metz (11) ve své práci ukázal, že tento bod na ROC křivce je bod, ve kterém sklon tečny splňuje následující rovnici:
kde C – čisté náklady na léčbu zdravých pacientů, B – čistý zisk z léčby nemocných pacientů a P(D+) – prevalence onemocnění.
Na první člen naší rovnice – na poměr C/B můžeme nahlížet negativně – pohled pouze na náklady (peněžní náklady, nežádoucí účinky léčby a kombinace obou předchozích) – potom pro tento poměr platí rovnice odvozena Metzem (11) a Weinsteinem a Finebergem (12):
nebo pozitivně – pohled na prospěch (peněžní úspory, zdravotní prospěch – zlepšení zdraví, kvality přežívání, nebo také kombinace obou předchozích) – a potom pro naše C/B platí rovnice odvozena Soxem (13):
Druhý člen naší rovnice je závislý na prevalenci onemocnění.
Abychom lépe pochopili vliv jednotlivých veličin na volbu optimálního dělícího bodu, uveďme si několik příkladů.
Prevalence
Uvažujme diagnostický test pro detekci hepatitidy B, který má senzitivitu i specificitu rovnou 0,99 a uvažujme dvě různé populace s počtem jedinců 10 000, a to populaci v Africe a v Číně, kde prevalence tohoto onemocnění podle (14) je 5–20% a druhou populaci v Evropě, kde prevalence je jenom 0,1–1%. Když si tato data vložíme do tabulky záměn, přičemž v první populaci vezmeme do úvahy hodnotu prevalence 20% a ve druhé hodnotu 0,1%, dostáváme tabulky 2 a 3.
Tab. 2. Skutečné počty pacientů (TP, FP, TN, FN) pro diagnostický test pro detekci hepatitidy B se senzitivitou a specificitou rovnou 0,99 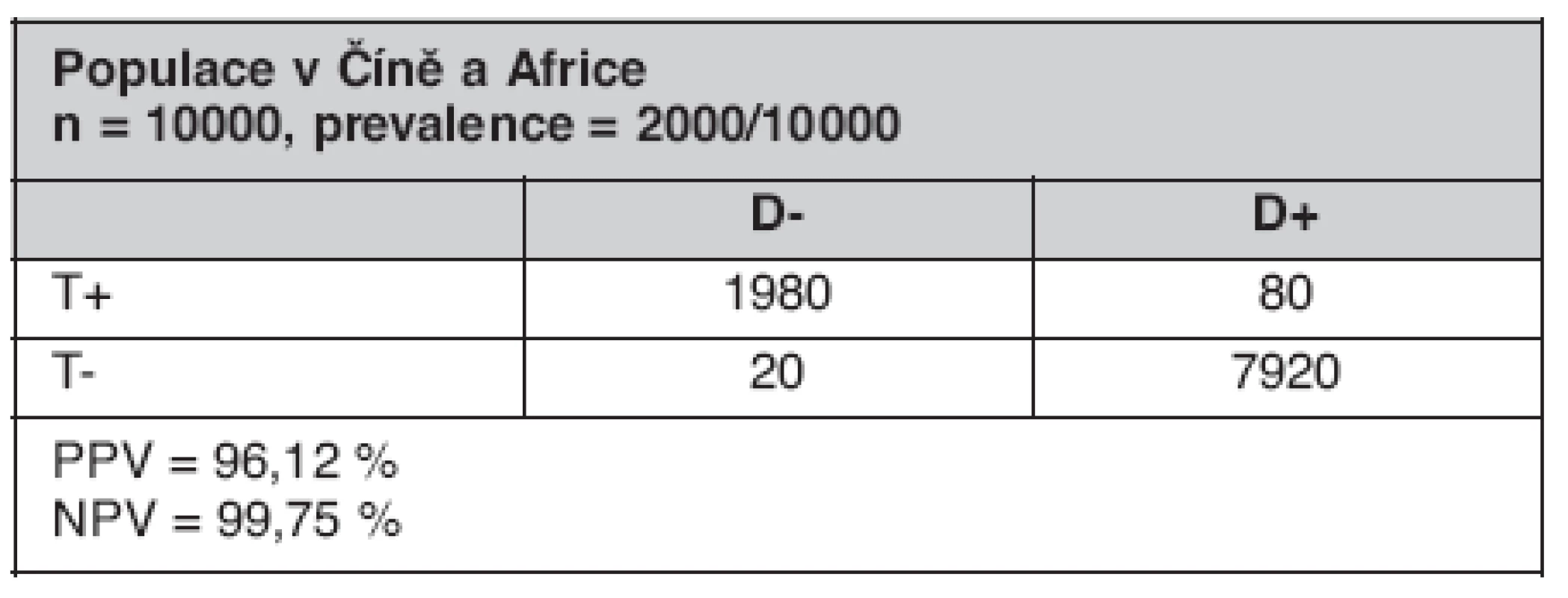
Tab. 3. Skutečné počty pacientů (TP, FP, TN, FN) pro diagnostický test pro detekci hepatitidy B se senzitivitou a specificitou rovnou 0,99 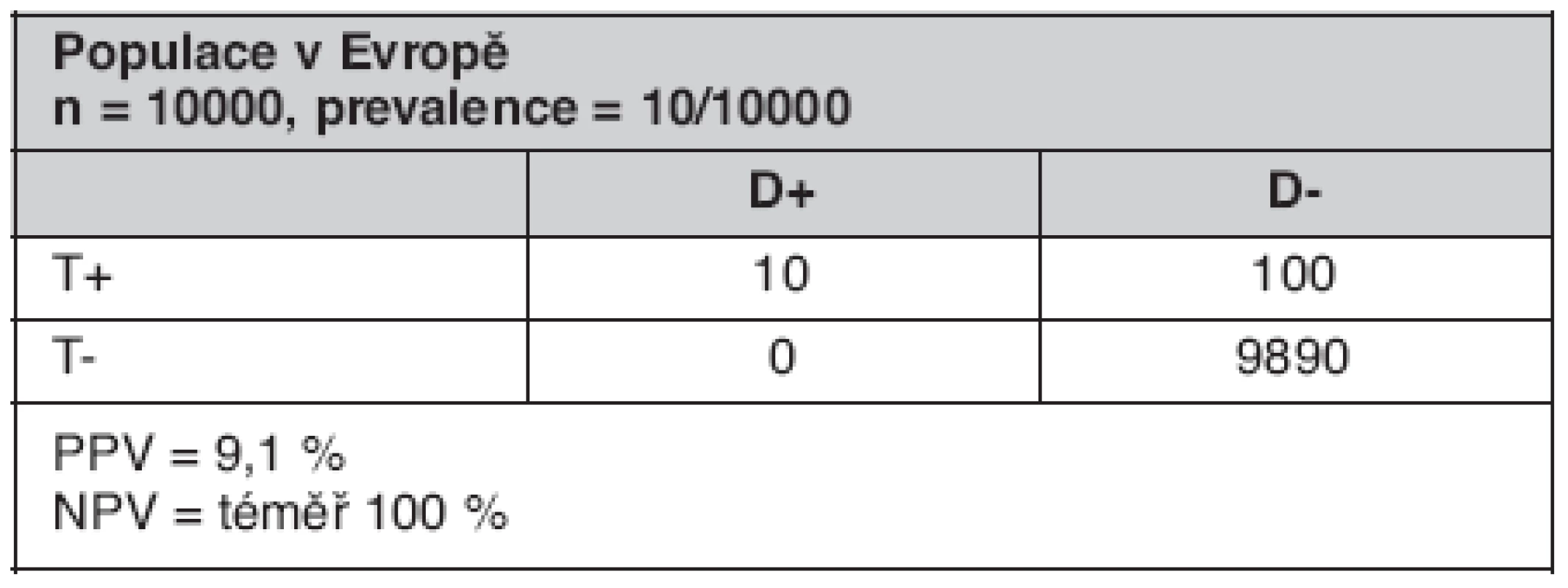
TP – pravdivě pozitivní, FP – falešně pozitivní, FN – falešně negativní, TN – pravdivě negativní, PPV – pozitivní prediktivní hodnota, NPV – negativní prediktivní hodnota Z těchto hodnot můžeme dopočítat pozitivní a negativní prediktivní hodnoty diagnostického testu.
Z rovnice pro výpočet optimálního bodu vidíme, že pro první populaci (obyvatelé Číny a Afriky, vysoká prevalence onemocnění) (tab. 2) je poměr
Z toho plyne, že sklon směrnice tečny je malý a bod bude ležet v pravém horním kvadrantu grafu ROC křivky (bod A na obrázku 1). Tento bod také označovaný jako „nedbalý práh“ minimalizuje počet falešně negativních, ale také naopak přináší větší počet falešně pozitivních. Avšak jak můžeme vidět z tabulky 2, obě hodnoty PPV i NPV jsou dostatečně vysoké, takže můžeme říci, že pokud je onemocnění běžné, je pozitivní test s velkou pravděpodobností pravdivě pozitivní. Tato skutečnost nám minimalizuje počet falešně pozitivních, a tedy nám nevadí zvolená poloha optimálního bodu v pravém horním kvadrantu.
Naopak pro druhou populaci (obyvatelé Evropy, nízká prevalence onemocnění) (tab. 3) platí pro poměr.
Sklon směrnice tečny je velký a náš bod bude ležet v levém dolním kvadrantu grafu (bod B na obrázku 1). Pokud zvolíme optimální bod v této oblasti, označujeme jej jako „přísný práh“. Tento zvolený bod přináší sice méně falešně pozitivních avšak na úkor velkého počtu falešně negativních. Z vypočtených hodnot PPV a NPV vidíme, že pokud je onemocnění vzácné, je i velmi specifický test svázán s mnoha falešně pozitivními případy. Proto naše volba optimálního bodu v této oblasti, kde ve skutečnosti je málo falešně pozitivních, je volbou správnou.
Druh léčby, testu
Obecně můžeme říci, že pokud je léčba nebo vyšetřovací metoda bolestivá, nebezpečná nebo toxická a navíc šance vyléčení tohoto onemocnění je malá, je poměr C/B, a tím i sklon tečny k ROC křivce velký a námi zvolený dělící bod bude ležet v levém dolním kvadrantu v oblasti tzv. „přísného prahu“. Naproti tomu, pokud je léčba i vyšetřovací metoda bezpečná a existuje velká šance vyléčení nemoci, je poměr C/B menší než 1, sklon tečny je mírný a námi zvolený dělící bod bude v tomto případě ležet v pravém horním kvadrantu. Abychom lépe pochopili volbu dělícího bodu pro tyto dva případy, uveďme si následující příklady.
Uvažujme pacienta se zhoubným onemocněním mozku (příklad byl převzat z literatury (10)). Pokud u diagnostického testu získáme pozitivní hodnotu, čeká pacienta velmi těžká operace, přičemž víme, že tato operace pacientovi s tímto onemocněním pomůže jen velmi málo. V případě negativního testu neděláme nic. Cena FP (operace na otevřeném mozku u zdravého pacienta) je obrovská oproti ceně TN (neděláme nic), čili CFP – CTN >> 1. Cena FN (neděláme operaci, která vlastně stejně pacientovi moc nepomůže) je velmi podobná ceně TP (téměř beznadějná operace), čili CFN – CTP→ 0, a tedy:
a náš bod leží v levém dolním kvadrantu.
Naproti tomu při apendicitidě při získání pozitivního testu, provádíme operaci, která není příliš nebezpečná, čili můžeme říci, že cena TP a cena FP je přibližně stejná. Cena TN je opět nulová (neděláme nic), avšak v případě falešné negativity může dojít k sepsi a k ohrožení života, někdy až k úmrtí pacienta, čili cena FN je obrovská. Takže CFP – CTN→ 0 a CFN – CTP >> 1, a tedy:
a náš bod leží v horním pravém kvadrantu.
Porovnání dvou diagnostických testů
Velmi často potřebujeme porovnat dvě různé diagnostické metody, které provádíme na stejném výběru pacientů, s cílem vybrat pro diagnostické účely tu nejlepší. K tomu používáme Z – statistiku, kterou podle Hanleyho a McNeila definujeme následujícím vztahem (15):
A1 a A2 jsou dvě plochy pod křivkou, SE1 a SE2 jsou odpovídající standardní chyby těchto ploch a r vyjadřuje korelaci mezi těmito plochami, která vzniká v důsledku použití obou metod nad těmi samými daty. V jiném případě je r = 0. Pro standardní chybu SE podle Hanleyho a McNeila platí:
A je opět plocha pod křivkou, nP je počet pozitivních výsledků, nN je počet negativních (normálních) hodnot a pro Q1 a Q2 platí:
Pokud námi spočtené Z je větší než kritická hodnota, nulovou hypotézu H – „Obě metody jsou stejné“ – zamítáme a přijímáme alternativní hypotézu HA – „Metody jsou rozdílné.“ Je potřeba zdůraznit, že statisticky nevýznamná hodnota testu neznamená implicitně rovnost mezi oběma metodami.
Závěr
Ve své práci jsme předložili krátký přehled o ROC analýze a o začlenění do ní analýzy nákladů a přínosů. Po definici základních veličin ROC analýzy, jako jsou senzitivita, specificita, PPV, NPV a plocha pod křivkou, jsme se v krátkém přehledu a na pár příkladech snažili vysvětlit použití analýzy nákladů a přínosů při volbě optimálního dělícího bodu. Vzhledem k tomu, že naše práce byla zaměřena na lékařský výzkum, základními veličinami ovlivňujícími naše rozhodování byly prevalence, závažnost onemocnění, toxicita léčby nebo diagnostického testu, nebo naopak přínos léčby pro pacienty.
Zkratky
AUC (AUROC) – plocha pod křivkou (area under the curve)
FN – falešně negativní (false negative)
FNR – falešně negativní poměr (false negative rate)
FP – falešně pozitivní (false positive)
FPR – falešně pozitivní poměr (false positive rate)
NPV – negativní prediktivní hodnota (negative predictive value)
PPV – pozitivní prediktivní hodnota (positive predictive value)
ROC – prahová operační charakteristika (receiver operating characteristic)
TN – pravdivě negativní (true negative)
TNR – pravdivě negativní poměr (true negative rate)
TP – pravdivě pozitivní (true positive)
TPR – pravdivě pozitivní poměr (true positive rate)
Tento článek vznikl za podpory výzkumného záměru MSM 0021620814 „Prevence, diagnostika a terapie diabetes mellitus, metabolických a endokrinních poškození.“
Adresa pro korespondenci:
Ing. Jana Vránová
Ústav lékařské biofyziky a lékařské informatiky 3. LF UK
Ruská 87, 100 00 Praha 10
e-mail: jana.vranova@lf3.cuni.cz
Zdroje
1. Egan JP. Signal Detection Theory and ROC Analysis, Series in Cognition and Perception. New York: Academic Press 1975.
2. Swets JA, Dawes RM, Monahan J. Better Decision through Science. Scientific American 2000; 283 : 82–87.
3. Beutel J, Kundel HL, van Metter RL. (eds) Handbook of Medical Imaging. Volume 1. Physics and Psychophysics. Bellingham, Washington: SPIE Press 2000.
4. Spackman KA. Signal detection theory: Valuable tools for evaluating inductive learning. In: Proceedings of the Sixth International Workshop on Machine Learning. San Mateo, CA: Morgan Kaufman 1989; 160–163.
5. Skalská H. Statistika a technologie data mining. Hradec Králové: 2000; habilitační práce.
6. Zavadil Z. Způsoby vyhodnocování kvality separace dvou a více množin, metody vizualizace výsledků, rešeršní práce. ČVUT FJFI, Katedra matematiky 2004.
7. Zvárová J, Hanzlíček P, Hejl J, Jirkovec Z, Pikhart H, Přibík V, Smitková V, Zvára K. Základy informatiky pro biomedicínu a zdravotnictví [online]. EuroMISE Centrum 2006, [cit. 2008-11-13], http://www.euromise.cz/education/textbooks/ biomedicinska_informatika.html.
8. Tape TG. Interpreting Diagnostic Tests [online], University of Nebraska Medical Center, [cit. 2008-11-13], http://gim.unmc. edu/dxtests/ROC3.htm.
9. Cantor SB, Sun CC, Tortolero-Luna G, Richards-Kortum, Follen M. A Comaprison of C/B Ratious from Studies Using Receiver Operating Characetrsistic Curve Analysis. J Clin Epidemiology 1999; 52 : 885–892.
10. The Magnificent ROC [online], [cit. 2008-11-13], http://www. anaesthetist.com/index.htm.
11. Metz CE. Basic Principles of ROC Analysis. Semin Nucl Med 1978; 8 : 283–298.
12. Weinstein MC, Fineberg HV. Clinical Decision Analysis. Philadelphia: W. B. Saunders 1980.
13. Sox HC, Blatt MA, Higgins MC, Marton KI. Medical Decision Making. Boston: Butterworths 1988.
14. Adam Z, Ševčík P, Vorlíček J, Mistrík M. Kostní nádorová choroba. Praha: Grada Publishing, a.s. 2005.
15. Hanley JA, McNeil BJ. A Method of Comparing the Areas under the Receiver Operating Curves Derived from the Same Cases. Radiology 1983; 148 : 839–843.
Štítky
Adiktologie Alergologie a imunologie Anesteziologie a resuscitace Angiologie Audiologie a foniatrie Biochemie Dermatologie Dětská dermatologie Dětská gastroenterologie Dětská gynekologie Dětská chirurgie Dětská kardiologie Dětská nefrologie Dětská neurologie Dětská onkologie Dětská otorinolaryngologie Dětská pneumologie Dětská psychiatrie Dětská radiologie Dětská revmatologie Dětská urologie Diabetologie Endokrinologie Farmacie Farmakologie Fyzioterapie Gastroenterologie a hepatologie Genetika Geriatrie a gerontologie Gynekologie a porodnictví Hematologie a transfuzní lékařství Hygiena a epidemiologie Hyperbarická medicína Chirurgie cévní Chirurgie hrudní Chirurgie plastická Chirurgie všeobecná Infekční lékařství Intenzivní medicína Kardiochirurgie Kardiologie Logopedie Mikrobiologie Nefrologie Neonatologie Neurochirurgie Neurologie Nukleární medicína Nutriční terapeut Obezitologie Oftalmologie Onkologie Ortodoncie Ortopedie Otorinolaryngologie Patologie Pediatrie Pneumologie a ftizeologie Popáleninová medicína Posudkové lékařství Praktické lékařství pro děti a dorost Protetika Psychologie Radiodiagnostika Radioterapie Rehabilitační a fyzikální medicína Reprodukční medicína Revmatologie Sestra Sexuologie Soudní lékařství Stomatologie Tělovýchovné lékařství Toxikologie Traumatologie Urgentní medicína Urologie Laboratoř Domácí péče Foniatrie Algeziologie Zdravotnictví Dentální hygienistka Student medicíny
Článek K diskuzi o etikoterapiiČlánek LAUREÁTI NOBELOVY CENY
Článek vyšel v časopiseČasopis lékařů českých
Nejčtenější tento týden
- Psilocybin je v Česku od 1. ledna 2026 schválený. Co to znamená v praxi?
- Alergie na antibiotika u žen s infekcemi močových cest − poznatky z průřezové studie z USA
- Není statin jako statin aneb praktický přehled rozdílů jednotlivých molekul
-
Všechny články tohoto čísla
- K diskuzi o etikoterapii
- ROC analýza a využití analýzy nákladů a přínosů k určení optimálního dělícího bodu
- Pocty pro členy české lékařské společnosti Jana Evangelisty Purkyně
- Analýza anamnestických dat a výsledků vyšetření v souboru 353 nemocných s plicním karcinomem z let 2004–2007
- Zmírňování koktavosti bronchodilatací β2 sympatomimetikem formoterolem
- Vydechovaný oxid dusnatý a jeho korelace s bioptickými nálezy u pacientů s chronickým kašlem
- Závažná kožní toxicita po léčbě ifosfamidem, gemcitabinem a vinorelbinem u pacienta s relapsem Hodgkinova lymfomu a ichtyózou
- Význam infekce pro tight junction
- Vztah mezi bariérou a antimikrobiálními peptidy
- Subakutní tyreoiditida zaměněna za zubní problém
- Spolek lékařů českých v Praze
- Chraňte děti před počítači a počítače před dětmi
- JAK SE HLÁSIT NA VZDĚLÁVACÍ AKCE IPVZ
- První desetiletí PET v důkazech Nemocnice Na Homolce, Praha, 4. září 2009
- 2. trilaterální sympozium s mezinárodní účastí Rožnov pod Radhoštěm, 17.–19. června 2009
- Olomoucké hematologické dny s mezinárodní účastí
- Seminář o metodologii výzkumu nikotinu a tabáku
- Zoonózy – nákazy s přírodní ohniskovostí
- 8. celostátní konference dětské pneumologie v Praze
- Blahopřání Mistru Josefu Sukovi k narozeninám
- LAUREÁTI NOBELOVY CENY
- Časopis lékařů českých
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- ROC analýza a využití analýzy nákladů a přínosů k určení optimálního dělícího bodu
- Subakutní tyreoiditida zaměněna za zubní problém
- Vydechovaný oxid dusnatý a jeho korelace s bioptickými nálezy u pacientů s chronickým kašlem
- Zoonózy – nákazy s přírodní ohniskovostí
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání






















