Individualization of head related transfer function

Summary

Head related transfer functions (HRTFs) are needed to present virtual spatial sound sources via headphones. Since individually measured HRTFs are very costly and time consuming, in this paper the individualization of the dummyhead’s HRTFs will be discussed. Here, the individualization is based on a scalable ellipsoidal head model. From this model the individualization is splitted into the individualization of the interaural time difference (ITD) and the spectral domain. The ellipsoidal modeling of the ITD gives quantitatively good results, considering the individual measurements. The second approach in spectral domain scales the transfer function in frequency. An angle dependent scaling factor is calculated by the head dimensions of the subject. Afterwards, the scaling results are compared and discussed with individual measurements.

Keywords:
binaural technology, virtual reality, HRTF

Introduction

In the past decades the binaural sound reproduction in virtual reality became more and more important. For synthesis, it is necessary to use head related transfer functions (HRTF) to create a plausible illusion of a virtual sound source in space. Spatial hearing, which is given by the HRTFs, is based on the fact that human beings hear binaurally. Thereby, they analyze interaural and spectral differences between sounds arriving at both ears.

An emitted sound wave is influenced by reflections on the physical dimension of the listeners head and torso before it arrives the inner ear. Those influences are characteristic for each direction of sound origin and make sound localization possible. Because the physical dimensions of every listener are individual, the HRTF is also individual. Every point in the room that is to be reproduced has its own transfer function. This entails that an individual measurement with a high spatial resolution is time consuming. Therefore, it is common to use the HRTF of a dummy head, which was developed to replicate the human HRTF. Unfortunately, dummy heads are not representative, if the torso, head and pinna dimensions deviate. Eventually, front-back confusions occur more often with the dummy head HRTF than with the individual one [1]. To compensate these localization problems without an individual measurement the idea of the present work is to individualize one given HRTF data set of the ITA (Institute of Technical Acoustics) dummy head based on individual head, torso and ear dimensions.

State of the art

A former publication which deals with the estimation of the ITD was published by Kuhn in 1977 [2]. His estimation is based on the approximation of the head by a sphere. The radius a of the sphere is defined by the half of the distance between the ears. His considerations trace back to the diffraction of a harmonic plane wave by a sphere with a hard surface. He distinguishes his elaboration for different frequency ranges. For lower frequencies where (ka)² << 1 is valid and the ITD is most important for localization, he deduces the frequencyindependent formula:

(1)

where k is the acoustic wave number, c₀ is the sound velocity and φ the position of the sound source given as azimuthal angle (see below).

To describe the total exterior sound field p_tot around a sphere the analytical solution that is derived in [3] is used. The total exterior field is described as the sum of the incident plane wave p_i (with amplitude p₀ = 1) and the scattered wave p_s:

(2)

(3)

(4)

where P_m (z) is the Legendre polynomial, j_m(z) is the spherical Bessel function and h²_m (z) is the spherical Hankel function of the second kind.

In the last two decades Duda and Algazi released several works that deal with the individualization of HRTF. They worked on a spherical head model [4] and on estimating the ITD of a mathematical description of the head as an ellipsoid [5] both considering anthropometrical data. The spherical model predicts the high-frequency ITD with a high accuracy and provides an empirical formula which uses an optimized sphere radius based on anthropometry. The ellipsoidal approach produces qualitatively better results than the spherical model, but underestimates the individual ITD of a subject. To compensate the underestimation they increased the head dimensions by 5 to 10%. To validate their customizations they collected anthropometric data and individual HRTFs of 45 subjects. Those were also combined in a database with public availability for further analysis of individual characteristics of HRTFs [6].

Middlebrooks worked on the individualization of HRTF by a scaling factor that is also based on various dimensions of the human head [7] [8]. His investigations began with the measurement of individual HRTFs of 34 subjects. Listening tests with other-ear HRTFs showed that localization errors increased with the intersubject spectral difference of HRTFs. There upon, an optimal scaling factor was calculated by minimizing spectral differences between the HRTFs of every possible combination of two subjects’ HRTFs. By comparing intersubject ratios of physical dimension with intersubject optimal scale factors, the strongest correlation occured for the pinna-cavity height and the head width. Linear regression led to the following empirical formula:

(5)

if subject A is larger than subject B, to scale subject A’s HRTF towards higher frequencies.

Localization cues

The duplex theory describes the combination of ITD and Interaural Level Difference (ILD) for lower and higher frequencies (below and above 2 kHz), respectively [9]. ITD and ILD are mainly important for localization on the horizontal plane (see fig. 1(a)). In the special case of the median plane, where ITD is zero due to the symmetry of the head (see fig. 1(b)). The elevation in the median plane can only be localized by spectral cues, induced by interferences in the human pinna and localization movements.

Individual Measurements

HRTF

Blauert defined the HRTF as the relation between the transfer path TF_earfrom a sound source to a microphone at the ear canal entrance and a reference measurement TF_center (eq. 6) [10]. The reference transfer path is measured from the same sound source location to a microphone at the position of the center of the head, when the head is absent. To obtain an HRTF with a high spatial resolution, this measurement has to be repeated at a discrete number of points in the room.

(6)

Coordinates

The coordinates are defined as spherical coordinates with the ears aligned to the y-axis and the nose to the x-axis. The z-axis points away from the vertex (fig. 2). The azimuthal angle φ is measured to the x-axis, while the elevation angle is measured to the z-axis. The position (ϑ, φ) = 0°, 0° is located directly above the vertex of the head, while (90°, 90°) refers to the position facing the left ear and (90°, 270°) facing the right ear.

Measurement Setup

To examine the differences between individual HRTFs individual measurements of four female and six male subjects and the ITA dummy head were carried out. The measurements were taken in the anechoic chamber of the Institute of Technical Acoustics. The measurement was realized by an arc on which 40 loudspeakers are positioned on the median plane that represent the elevation angles from ϑ = 2.8° to ϑ = 147° in steps of approximately 3.7° (fig. 3). The arc can be adjusted so that the subject’s head is in the center. The subject’s ear and the center of the arc are aligned by a laser tool. The subject stands on a rotating plate, while the arc is fixed. For the measurement of the individual transfer functions two measuring microphones are positioned at the entrance of the ear canals and the subject is constantly rotated on the plate in 5° steps from φ = 0° to 355°. Using interleaving sweeps as excitation signal allows to measure the HRTF at each azimuthal position for 40 positions in elevation at once [11]. The measurement of one HRTF set for 72 azimuth angles and 40 elevations lasts about six minutes [12] [13].

Anthropometrical Data

To be able to compare the individually measured with the individualized data, several dimensions of the subject’s heads are taken (see tab. 1). First measurements to be taken are the width w, the depth d and the height h (see section 3). The width is taken with a caliper. The depth and height are taken through the contour from ear to ear along the nose and along the vertex, respectively. These contours U_height and U_depth are taken with a tape measure. Considering the contour as an ellipse makes it possible to calculate the depth d and the width w by the following approximation of the circumference of an ellipse (eq. 6). For ellipses that are calculated with the given head dimensions this approximation deviates under 1% from the accurate solution [14].

(7)

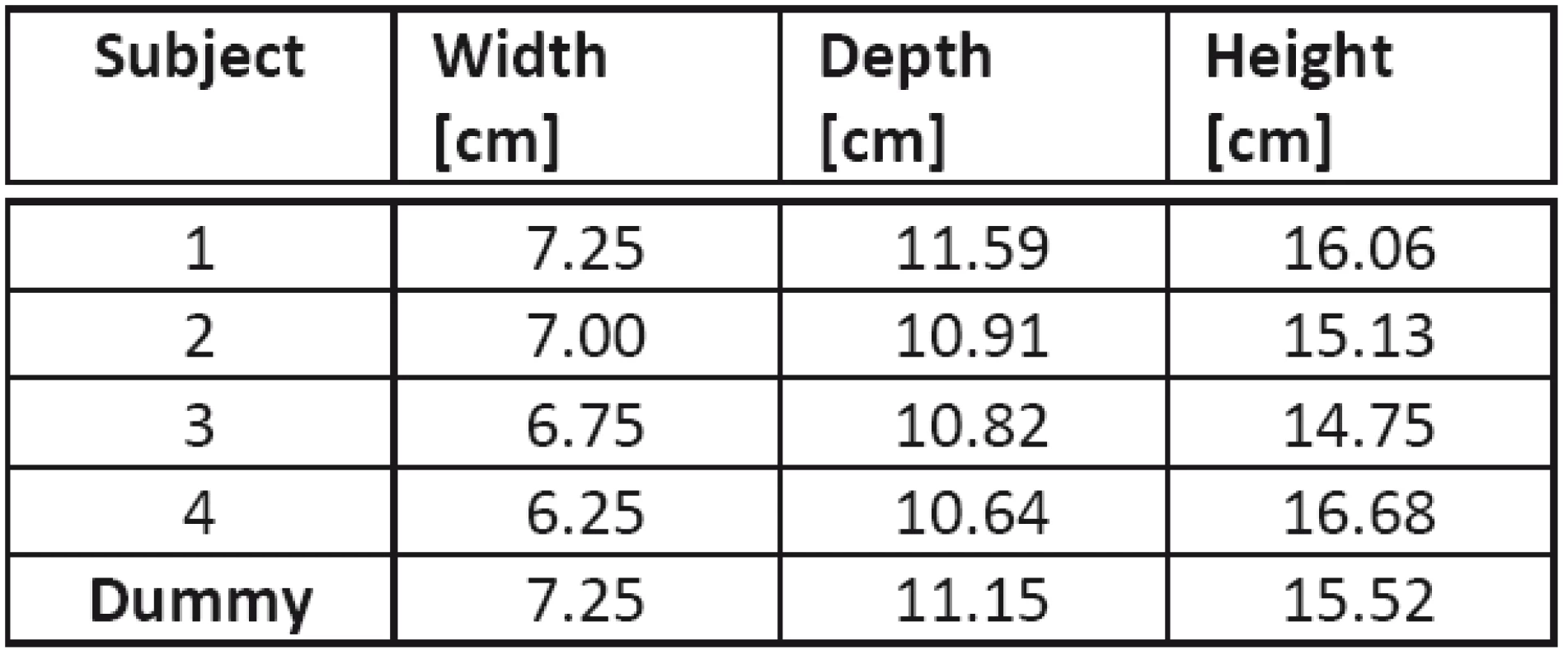
ITD adjusting

At first, the ITD of the dummy head should be scaled. In a rough estimation for low frequencies the head can be approximated by a sphere. The sound fields around the sphere can be described analytically [3]. The ITD is calculated by the phase from the analytical solution of the pressure and is thereby frequency dependent (eq. 8). The Interaural Phase Difference (IPD) results from the difference between the phases of the sound spectra at the left and the right ear.

(8)

where ω is the angular frequency defined by ω = 2πf  [2].

Ellipsoidal Approximation for ITD

Since the head’s approximation is better as an ellipsoid for lower frequencies (see table of individual measurements, table 1), the spherical radius of the analytical solution for the sound pressure will be angle dependent. This ellipsoid has three dimensions (width w, height h and depth d) which are determined from the subject’s head (tab. 1). Half the distance between the ears is defined as width w, the distance between the center of the head (on ear level) and nose is defined as depth d and the distance from the center to the vertex is given as height h.

The idea of combining the spherical approach with an ellipsoidal model is mainly based on the detour the sound makes on its way to both ears. For each position φ, for example on the horizontal plane, the detour s on an ellipsoid from the sound source to both ears is calculated by equation 9 where φ₁and φ₂ are the positions of the considered ear and of the source, respectively [15].

(9)

(10)

(11)

The radius of a sphere on which the sound would cover the same detour coming from the selected position φ is calculated (see equations 10 and 11) by equating s_ellipse with s_circle. That leads to two different sphere radiuses, one for each ear. Only on the median plane the detour is the same to both ears and the spherical radius for both ears is equal. There is also the special case where at the incident angles φ = 90° and φ = 270° the sound reaches one of the ears directly. At these positions the sound does not make any detour on the head to the nearest ear and the radius for the sphere of this ear does not influence the direct sound. As it is not possible to calculate a radius without detour, on this position it is decided to set this radius to the same value as on the nearest position.

An analytic acoustic simulation with the Boundary Element Method (BEM) of an ellipsoid with dimensions w, d and h validates the approximation through the spherical data to calculate ellipsoidal data.

For sound source positions that deviate from the horizontal plane the detour of the sound is described by the ellipse that results from the intersection of the ellipsoid and a plane that is held by the points of both ears and of the sound source. The red point in figure 4 demonstrates the position of the right ear.

Figure 5 shows the ITD that results from the individually measured HRTF for different elevation angles. As the irregularities (the subjects’ ITD curves are not as smooth as the dummy data) in the measurements for subject one to four show, it was difficult for the subjects not to move during the measurement despite a built-in neck rest. Therefore, the movement in the ITD in figure 5 is compensated by a constant angle shift.

On elevation angles near the horizontal plane the influence of the head radius is best to see. The head with the biggest radius also provides the largest ITD values and vice versa. On higher elevations the influence of the head dimensions on the ITD is lower but measurement uncertainties due to the subject’s motion increase.

The individualized ITD that was approximated by the ellipsoidal model contains outliers at positions near ϑ ≈ 90° and φ = 90°. These can be explained by the fact that the intersection line does not describe the shortest detour to the contralateral ear. At those positions the detour takes course along the upper side of the head instead of the front, causing the excessive ITD. For the same reason at the remaining elevations the ITDs also seem to be overestimated.

To compensate these overestimations it was decided to set h = d. As the height h of the head does not seem to have a large influence on the actual ITD, this is a fair compromise. Figure 6 shows that this approximation enhances the analytically calculated ITD.

So far the ellipsoidal model and the individual measurements seem to be well matched.

Frequency Scaling

In this chapter the frequency domain is scaled to improve the localization by monaural cues. The frequency scaling is influenced by [8]. From the fact that the shape of the HRTF depends on the head geometry it can be deduced that with larger head dimension the spectral characteristics of the HRTF tend to lower frequencies, while smaller head dimensions lead to spectral cues at higher frequencies. Therefore, the idea for individualization of a given HRTF set is to introduce a scaling factor similar to the one Middlebrooks establishes. If the subject’s head is greater than the dummy head the scaling factor k has to be smaller than 1. For scaling to a smaller head the scaling factor has to be greater than 1. This scaling factor is defined as the ratio of the elliptic radiuses for the selected position (see fig. 7 and equation 12 and 13).

(12)

(13)

Compared to Middlebrooks’ solution the scaling factor in formula 12 is angle dependent. It includes that the subject’s head deviates from the dummy head considering width or depth. Hereby, the radiuses at every position on the horizontal plane and the resulting scaling factor are calculated, as can be seen in fig. 8. Fig. 9 shows how the scaling factor for one direction shifts the entire transfer function on the whole frequency range higher frequencies. In figure 9 subject 4 is exemplary chosen. For this subject the HRTF is shifted to higher frequencies because the subject’s head was smaller than the dummy head. As the scaling factor shifts the HRTF to a higher frequency region, maxima and notches in the range of 4-6 kHz and 14 kHz of the individual and the scaled HRTF match much better in their position in frequency than without scaling. However, the maximum around 2 kHz should better be scaled to lower frequencies. Furthermore, in the diagram can be seen that the scaling factor does not modify the amplitude of the transfer function so that the maxima do not overlap. This should also be a factor to be considered, because the ILD is relevant for localization as well.

Conclusion and Outlook

The present paper gives a short overview of the implementations of individualizations of an HRTF that were done in the past and shows new approximations. The first part concentrates on the adaption of the ITD, for localization in the azimuthal range. At first, the sound propagation on a sphere is described analytically. Secondly, the sound propagation on an ellipsoid is derived from the first approach. Fig. 10 shows different approaches to model the ITD. The yellow line represents equation 1, that was assumed by Kuhn for ITD at lower frequencies. The light blue line shows the attempt to calculate the mentioned eq. 1 with the angle dependent radius, see eq. 13. However, the analytical ellipsoidal method seems to be the best to describe the measured ITD, as their curves overlap well. Despite this good accordance between the measurement and the calculated ITD, listening tests have to be done to confirm the model.

For further individualization an angle dependent scaling factor based on the radius of the head (eq. 12) was introduced. Although the scaling factor k has now an angle dependency, it does not seem to be the optimum way to scale an HRTF. The spectral cues of the HRTF do not only depend on one single dimension of the head, like the radius that is used for scaling, but also on the dimension of the shoulder and the pinna, which both have influence on different frequency ranges. The distance between ear and shoulder is one of the largest dimensions around the head (about 17cm) and leads to constructive sound interferences at lower frequencies (< 1 ‒ 2 kHz) depending on the exact distance. Otherwise the reflections on the dimensions of the pinna lead to interferences at higher frequencies. This gives rise to the fact that a listener’s HRTF whose ears are smaller than the ones of the dummy head and whose neck is longer, had to be scaled to two different directions in different frequency ranges.

Therefore, a scaling factor that is not only angle dependent, but also frequency dependent, considering different dimensions of the listener is contemplated. Most important to be adjusted are the spectral cues at higher frequencies, but the adjusting of pinna dimensions is much more complex than only defining one scaling factor by one dimension of the pinna. The pinna has inner convolutions that are important for localization, especially to detect the elevation of a sound source.

As replacement for the individualization by frequency scaling there is the concept of representing the dummy head HRTF by modal superposition. If the modes can be assigned to the corresponding physical dimensions, particular modes could be shifted. By the shifted modes a new transfer function can be calculated. Therefore, the measured HRTFs have to be tested for a coherence between physical dimensions and positions of poles. There are few publications that relate to modal superposition of HRTFs (see for example [16]). A similar approach could be translated to the individualization HRTFs.

Acknowledgement

The work presented in this paper was supervised by Prof. Dr.-Ing. Janina Fels and Prof. Dr. rer. nat. Michael Vorländer at the Institute of Technical Acoustics of RWTH Aachen. All simulations and measurements were done using the ITAToolbox (www.ita-toolbox.org) [17] in MATLAB. Technical assistance was kindly offered by Martin Guski and Stefan Zillekens.