-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Analýza dat v neurologii
XXVI. Hodnocení diagnostických testů – věrohodnostní poměr a diagnostický poměr šancí
Autoři: L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Působiště autorů: Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2011; 74/107(2): 221-225
Kategorie: Okénko statistika
V minulém díle seriálu jsme otevřeli novou kapitolu zaměřenou na hodnocení diagnostických testů. Představili jsme nové ukazatele správnosti a diagnostické síly testů, které produkují binární data (výstupy typu ano/ne; zdravý/nemocný apod.). Zároveň jsme doložili, že žádný jednotlivý ukazatel nepřináší zcela vyčerpávající informaci o kvalitě testu, a je tedy vysoce doporučeno je kombinovat. Krátce připomeňme hlavní ukazatele a jejich význam:
- Senzitivita: schopnost testu správně diagnostikovat nemocného člověka. Vyjadřuje pravděpodobnost, že test bude pozitivní u skutečně nemocných lidí. Počítáme ji jako podíl počtu pozitivních výsledků testu u nemocných a celkového počtu nemocných lidí.
- Specificita: schopnost testu negativně vyhodnotit zdravé pacienty. Vyjadřuje pravděpodobnost, že test bude negativní u zdravých lidí. Počítáme jako podíl počtu negativních výsledků testu u zdravých jedinců a celkového počtu zdravých lidí.
- Pozitivní prediktivní hodnota: podíl správně pozitivních výsledků ze všech pozitivních výsledků testu. Vyjadřuje pravděpodobnost, že člověk je skutečně nemocný při pozitivním testu.
- Negativní prediktivní hodnota: podíl správně negativních výsledků ze všech negativních výsledků testu. Vyjadřuje pravděpodobnost, že člověk je zdravý při negativním testu.
V tomto díle rozšíříme výše uvedenou sadu ukazatelů o tzv. věrohodnostní poměr („likelihood ratio“, LR). Věrohodnostní poměr je podílem pravděpodobnosti výskytu jevu 1 za platnosti určité podmínky (jev 2 nastal) a pravděpodobnosti výskytu jevu 1, pokud daná podmínka neplatí (jev 2 nenastal). Z diagnostického hlediska tak hodnotíme věrohodnost, že výskyt sledovaného klinického znaku (symptomu) je vázán na výskyt určitého onemocnění. V matematické statistice věrohodnostní poměr obecně znamená podíl dvou pravděpodobností, které jsou výsledkem dvou různých modelů.
Pro hodnocení diagnostických testů můžeme věrohodnostní poměr definovat následovně:
[pravděpodobnost, že test dosáhne daného
výsledku u nemocných pacientů]
LR = --------------------------------------------------
[pravděpodobnost, že test dosáhne
daného výsledku u zdravých osob]V našem hodnocení může diagnostický test nabídnout pouze dva typy výstupů, pozitivní a negativní. Rozlišujeme tedy LR+ (LR pro pozitivní test) a LR – (LR pro negativní test):
- Pro pozitivní výstup testu vyjadřuje LR podíl pravděpodobnosti, že nemocný pacient je testem diagnostikován jako pozitivní, a pravděpodobnosti, že zdravý pacient je chybně diagnostikován jako pozitivní.
LR+ = senzitivita / (1 – specificita)
- Pro negativní výsledek testu LR vyjadřuje podíl pravděpodobnosti, že nemocný pacient je testem chybně diagnostikován jako negativní, a pravděpodobnosti, že zdravý pacient je diagnostikován jako negativní.
LR– = (1 – senzitivita) / specificita
Věrohodnostní poměr značený jako LR+ tedy vyjadřuje schopnost pozitivního výsledku testu odlišit nemocného a zdravého jedince. Naopak věrohodnostní poměr značený jako LR – vyjadřuje obrácenou situaci, kdy test mylně označí nemocného jedince za zdravého (viz příklad 1). Z definice tedy vyplývá, že u kvalitního testu je LR+ žádoucí co nejvyšší a naopak LR – co nejnižší. V literatuře lze najít zdůvodnění, že hodnoty LR+ > 10 a naopak hodnoty LR – < 0,1 umožňují věrohodné určení nebo vyloučení nemoci na základě daného testu (McGee, 2002). Vysoká hodnota LR+ jasně ukazuje na test, který poskytuje vysokou jistotu v určení nemoci, i přesto však není 100% zárukou, že osoba s pozitivním testem musí být vždy nemocná.
Příklad 1. Výpočet věrohodnostního poměru pro hodnocení diagnostického testu. 
Výpočet věrohodnostního poměru pro různé výsledky diagnostického testu přibližují příklady 1 a 2. I věrohodnostní poměr je odhadem, a lze jej tedy doplnit výpočtem intervalu spolehlivosti, jak dokládá příklad 3. Ačkoli jsou vztahy v příkladu 3 na první pohled poněkud složité, lze do nich jednoduše dosadit hodnoty z tabulky četností a interval spolehlivosti tak vypočítat.
Příklad 2. Hodnocení výsledků různě citlivých diagnostických testů a výpočet věrohodnostního poměru. 
Příklad 3. Odhad věrohodnostního poměru a jeho intervalu spolehlivosti. 
Věrohodnostní poměr je často používán pro srovnávání výstupů různých testů, přičemž je souhrnně kalkulován tzv. diagnostický poměr šancí („Diagnostic Odds Ratio“, DOR). DOR vyjadřuje šanci, že test bude pozitivní u nemocného člověka násobenou šancí, že test bude negativní u zdravého člověka.
DOR = LR+ / LR–
Hodnota DOR může růst od 0 do nekonečna, přičemž vyšší hodnoty znamenají lepší schopnost testu rozlišovat mezi nemocnými a zdravými jedinci, a tedy obecně větší schopnost dosahovat správného výsledku. Hodnoty menší nebo rovny 1 ukazují na test se slabou diagnostickou silou. Logicky požadujeme, aby diagnostický poměr šancí byl co nejvyšší a zejména hodnoty 1 a nižší nejsou pro klinickou praxi přijatelné.
Pojem šance (odds) je blízký pojmu věrohodnostní poměr a vztahuje se k pravděpodobnosti, že nějaký jev nastane. Ačkoli v českém jazyce možná slovo šance nezní příliš exaktně, jde o jasně definovaný pojem, který se i v medicíně velmi často používá. Šanci, že nějaký jev nastane, vyjadřujeme i v běžné řeči formou poměru, například šance výskytu jevu A je 1 ku 4. To znamená, že jev A nastává s pravděpodobností P(A) = 1 / 5 = 0,20. Šanci nastání jevu A označujeme O(A) (odds). Pro náhodný jev A potom obecně platí:
P(A)
O(A) = --------
1 – P(A)Výše uvedený vztah také někdy čteme jako „šanci ve prospěch A“. Ze vztahu je patrné, že šance je podíl pravděpodobnosti nastání jevu A „ku“ pravděpodobnosti nenastání jevu A. Pokud pravděpodobnosti přímo odhadujeme z relativních četností jevů, např. z kontingenční tabulky, pak můžeme do vztahu dosadit přímo četnosti nastání jevu A a četnosti nenastání jevu A:
četnost jevu A
O(A) = ------------------------------
četnost nenastání jevu AŠance dvou jevů lze dávat do poměru, hovoříme o poměru šancí („odds ratio“). Ten může nabývat nejnižší hodnoty 0, v maximu ale nijak ohraničen není.
Vedle věrohodnostního poměru a diagnostického poměru šancí lze v literatuře najít i další ukazatele kvality diagnostických testů, které ale povětšinou vycházejí z odhadu senzitivity a specificity. Zde se pouze krátce zmíníme o dvou ukazatelích, jejichž výpočet i interpretace jsou velmi jednoduché:
- Dosažená jistota („gain in certainty“) kalkulovaná jako prostý součet specificity a senzitivity (Connell a Koepsell, 1985). Součet může nabývat hodnot od 0 do 2, přičemž hodnoty blízké 1 indikují test, jehož výsledky odpovídají náhodnému tipování. Sčítání hodnot senzitivity a specificity je vhodné pro srovnávání různých testů, zvláště pokud byly testovány při různé prevalenci dané choroby.
- Jinou, podstatně starší mírou je tzv. Youdenův index (Youden, 1950), značený „J“ = senzitivita + specificita – 1. Tento výpočet lze alternativně vyjádřit jako 1 – (falešná pozitivita + falešná negativita)
Výpočty věrohodnostního poměru, diagnostického poměru šancí a dalších ukazatelů diagnostické hodnoty testu shrnuje pro různé datové soubory tab. 1.
Tab. 1. Ukázky výpočtu různých ukazatelů správnosti diagnostických testů<sup>1</sup> 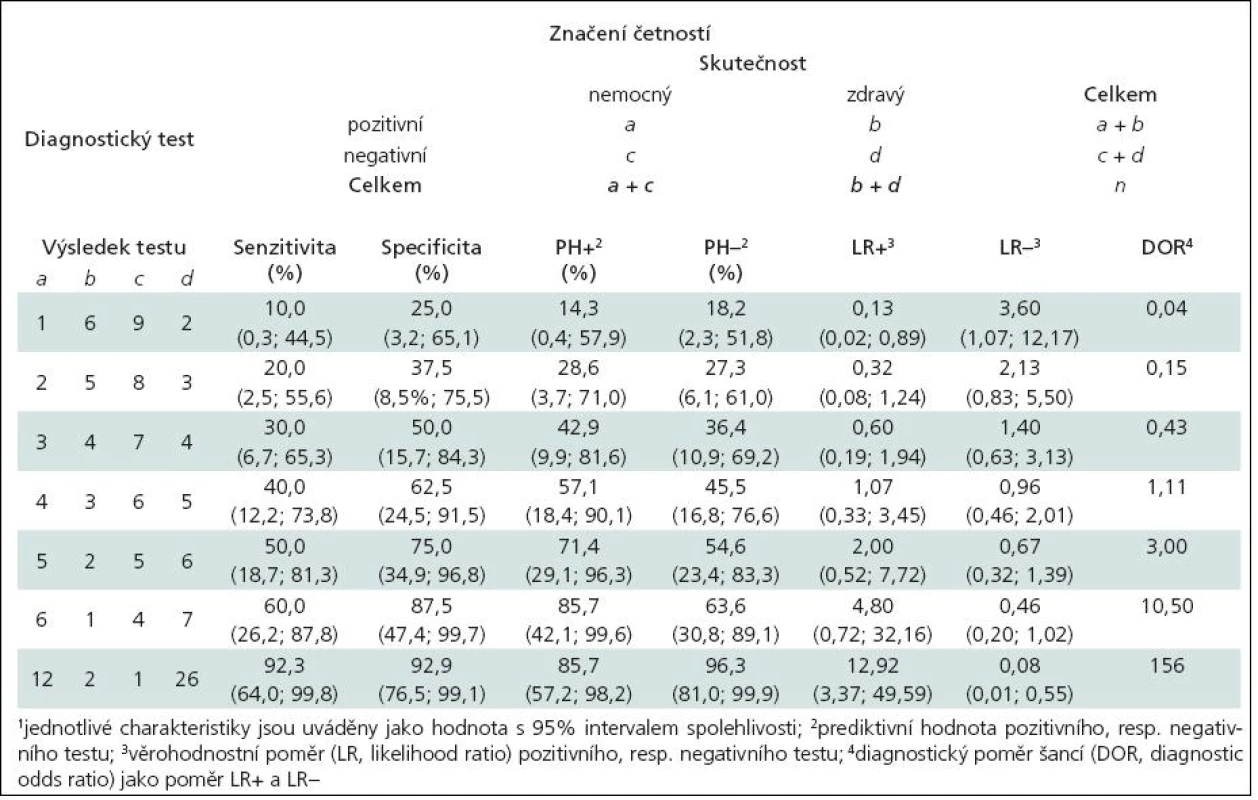
Věrohodnostní poměr, jakož i další zmíněné míry nabízejí alternativní vyjádření hodnoty diagnostických testů k hodnocení senzitivity a specificity. Je samozřejmě na autorovi, zda využije všechny tyto míry souběžně či nikoli. Čtenáře jistě napadne zcela legitimní otázka, není-li ukazatelů kvality testu příliš mnoho a jestli skutečně přispívají k interpretaci. Pravdou je, že žádný ukazatel nedá svou hodnotou 100% záruku, že při pozitivním testu je pacient skutečně nemocný. Výsledek je ovlivňován řadou faktorů, mimo jiné i velikostí testovacích souborů dat a způsobem jejich získání. I tyto faktory jsou důvodem vývoje různých ukazatelů, které nabízejí různé interpretace hodnoty testů. V literatuře nalezneme i prospektivní randomizované studie, jež řeší, zda jsou lékaři v praxi schopni správně využívat ukazatele kvality diagnostických testů pro svá rozhodování. Například práce Puhana et al z roku 2005 takto srovnávala senzitivitu a specificitu s věrohodnostním poměrem a došla k závěru, že jsou ve svém vlivu na rozhodování lékařů srovnatelné. Nicméně věrohodnostní poměr je stále poměrně málo využíván při praktické validaci diagnostických testů (Steurer et al, 2002). Obdobně i diagnostický poměr šancí by si zasloužil častější aplikaci především pro svou jasnou interpretaci (Ingelfinger et al, 1987).
Tento díl seriálu jsme pojali více i jako rešerši relevantní literatury a výklad dokládáme větším počtem citací vědeckých prací. Udělali jsme to záměrně, abychom upozornili na překvapivý fakt, jak je svým způsobem velmi staré a jednoduché téma v současné literatuře živé. Důvodem je z velké části medicína sama. S nástupem personalizované medicíny přichází na trh velké množství nových biomarkerů a s nimi také roste heterogenita a cena diagnostických testů. Srovnávání různých testů je tedy velmi aktuální téma řešené z hlediska diagnostické síly i nákladové efektivity (Cornell et al, 2008; Hayen et al, 2010). Jde o trend, který bude s rozvojem genomiky a farmakogenomiky jistě pokračovat. Je stimulující vidět, že i v dnešním přetechnizovaném a složitém světě lze publikovat významnou vědeckou práci prostou diskuzí nad součtem dvou pravděpodobností :).
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
Connell FA, Koepsell TD. Measures of gain in certainty from a diagnostic test. Am J Epidemiol 1985; 121(5): 744–753.
Cornell J, Mulrow CD, Localio AR. Diagnostic test accuracy and clinical decision making. Ann Intern Med 2008; 149 (12): 904–906.
Hayen A, Macaskill P, Irwig L, Bossuyt P. Appropriate statistical methods are required to assess diagnostic tests for replacement, add-on, and triage. J Clin Epidemiol 2010; DOI:10.1016/j.jclinepi.2009.08.024. PMID 20079607.
Ingelfinge, JA, Mosteller F, Thibodeau LA, Ware JH. Biostatistics in Clinical Medicíně. 2nd ed. New York: Macmillan 1987.
McGee S. Simplifying likelihood ratios. J Gen Intern Med 2002; 17(8): 646–649.
Puhan MA, Steurer J, Bachmann LM, ter Riet G. A randomized trial of ways to describe test accuracy: the effect on physicians‘ post-test probability estimates. Ann Intern Med 2005; 143(3): 184–189.
Sackett DL. Interpretation of diagnostic data: 5. How to do it with simple maths. Can Med Assoc J 1983; 129(9): 947–954.
Simel DL, Samsa GP, Matchar DB. Likelihood ratios with confidence: sample size estimation for diagnostic test studies. J Clin Epidemiol 1991; 44(8): 763–770.
Steurer J, Fischer JE, Bachmann LM, Koller M, ter Riet G. Communicating accuracy of tests to general practitioners: a controlled study. BMJ 2002; 324(7341): 824–826.
Youden WJ. Index for rating diagnostic tests. Cancer 1950; 3(1): 32–35.
Štítky
Dětská neurologie Neurochirurgie Neurologie
Článek Syndrom neklidných nohouČlánek Hyperkinetická porucha/„Attention Deficit Hyperactivity Disorder“ u dětských pacientů s epilepsiíČlánek SOUTĚŽ ČNSČlánek Oboustranná neurochorioretinitis na podkladě syfilis u 33leté uživatelky pervitinu – kazuistikaČlánek Náhle vzniklá dušnost jako příznak vedoucí k diagnóze amyotrofické laterální sklerózy – kazuistikaČlánek Webové okénko
Článek vyšel v časopiseČeská a slovenská neurologie a neurochirurgie
Nejčtenější tento týden
2011 Číslo 2- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Magnosolv a jeho využití v neurologii
- Zolpidem může mít širší spektrum účinků, než jsme se doposud domnívali, a mnohdy i překvapivé
- Nejčastější nežádoucí účinky venlafaxinu během terapie odeznívají
-
Všechny články tohoto čísla
- Syndrom neklidných nohou
- Využití kombinace metod magnetické rezonance pro diagnostiku tumorů
- Hyperkinetická porucha/„Attention Deficit Hyperactivity Disorder“ u dětských pacientů s epilepsií
- Invazivní mykotické sinusitidy
- Léčba kraniosynostóz remodelační technikou
- SOUTĚŽ ČNS
- Hluboká mozková stimulace u nemocných s extrapyramidovými poruchami pohybu – stereotaktická procedura a intraoperační nálezy
- Operační léčba poranění peroneálního nervu
- Radioterapií indukované meningeomy
- Oboustranná neurochorioretinitis na podkladě syfilis u 33leté uživatelky pervitinu – kazuistika
- Neurodegenerácia asociovaná s pantotenátkinázou – kazuistika
- Progredující axonální senzitivně-motorická multifokální polyneuropatie u pacientky s chronickou hepatitidou C
- Virus hepatitidy C a nervový systém: Komentář k práci Ambler et al Progredující axonální senzitivně-motorická multifokální polyneuropatie u pacientky s chronickou hepatitidou C
-
The Greenberg Rapid Review. A Companion to the 7th Edition
L. I. Kranzler. - Pacient s Creutzfeldtovou-Jakobovou nemocí se sníženým prokrvením mozku na Tc-99 ECD SPECT v počátcích choroby
- Náhle vzniklá dušnost jako příznak vedoucí k diagnóze amyotrofické laterální sklerózy – kazuistika
- Webové okénko
-
Analýza dat v neurologii
XXVI. Hodnocení diagnostických testů – věrohodnostní poměr a diagnostický poměr šancí - Průběh a závěry mezioborového setkání „Winter GLIO TRACK Meeting“ 2011
- Vzpomínky na neurology, s nimiž jsme rádi spolupracovali
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Syndrom neklidných nohou
- Operační léčba poranění peroneálního nervu
- Náhle vzniklá dušnost jako příznak vedoucí k diagnóze amyotrofické laterální sklerózy – kazuistika
- Invazivní mykotické sinusitidy
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



