Krev není voda: Fyzikální limity analýzy krevních stříkanců

Souhrn

Jednou z úloh analýzy krevních stříkanců je co nejpřesnější odhad místa, odkud vystříkla krev. Procesy vedoucí ke vzniku krevního stříkance jsou komplikované fyzikální jevy. K jejich kvantitativnímu popisu jsou používány modely, které jsou v posledních létech řešeny na počítačích. Příliš detailní modely jsou pro primární odhad místa, odkud krev vystříkla, téměř nepoužitelné. Z toho důvodu se používají zjednodušující modely vnášející do odhadu větší nejistotu. Volba modelu i stanovení nejistoty představují nedílnou součást výsledku.

Klíčová slova:

analýza krevních stříkanců – biomechanika

Analýza krevních stříkanců (BPA, z anglického Bloodstain Pattern Analysis) je obor na pomezí kriminalistické techniky a soudního lékařství. Základní myšlenka, ze které BPA vychází, je poměrně jednoduchá a přímočará. Předpokládá se, že charakter krevních stříkanců obsahuje informaci o ději, který vedl k jejich vzniku. Pro praktické účely je zajímavá zejména informace o způsobu vzniku krevních stříkanců, o charakteru zraňujícího předmětu a o časové posloupnosti dějů na místě činu. Analýza krevních stříkanců není nikterak novou disciplínou, již na konci 19. století se formováním krevních stříkanců zabýval Dr. E. Piotrowski působící na univerzitě v Krakově. Byl autorem první moderní práce (On the formation, form, direction, and spreading of blood stains after blunt trauma to the head, 1895) zabývající se danou problematikou. V první polovině 20. století se objevují další sporadické práce v Německu a ve Francii, i když ke zformování BPA jako svébytného oboru dochází až v 50. letech 20. století v USA zásluhou zejména H. L. MacDonella (1,2). Současné postoje odborné veřejnosti jsou odlišné – zatímco v USA je BPA samostatný obor se zajištěným specializačním vzděláváním, v ČR zaujímá odborná veřejnost spíše rezervovaný postoj k využití BPA jako běžného nástroje zkoumání průběhu úrazového děje (3).

Oblastí zájmu BPA jsou jakékoliv krevní stopy. Zdrojem užitečných informací mohou být krevní tratoliště, krevní stříkance i stopy od krve odkapávající nebo setřené z libovolných předmětů. Jednou z nejzajímavějších aplikací BPA je určení místa, ze kterého se krevní stříkance rozlétly (PO, z anglického Point of Origin). Může se jednat o směrovou analýzu, kdy se odhaduje pouze směr, ze kterého krevní stříkance přilétly, nebo může jít o odhad úplného prostorového umístění PO (1).

Směrová analýza je v zásadě velmi prostá. Krevní stříkanec má bez ohledu na objem a rychlost letící kapky krve více či méně protáhlý tvar, jehož dlouhá osa (největší rozměr) leží ve směru letu krevní kapky. Za vhodných podmínek lze zjistit polohu PO jako průsečík dlouhých os několika krevních stříkanců. Pokud jde o stanovení úplné polohy PO, tedy i výšku PO v prostoru, je situace mnohem složitější, protože je nutné odhadnout taktéž charakter trajektorie krevní kapky. V tomto případě je potřeba použít řadu zjednodušení fyzikální reality, které se mohou podílet na zkreslení odhadu trajektorie letící kapky krve. V následujících odstavcích se pokusíme nastínit fyzikální podstatu některých zkreslujících faktorů a případně načrtnout, jak významným způsobem se může jejich zanedbání podílet na zkreslení odhadu PO. Dále se pokusíme ukázat, jakým způsobem se PO odhaduje v praxi, protože vlivem řady zkreslujících faktorů je odhad PO z jediného stříkance krve zatížen tak velkou nejistotou, že jde v zásadě jen o hrubý odhad.

KREV JAKO KAPALINA

Základní vlastnosti kapalin

Jednou z důležitých vlastností reálných kapalin je vnitřní napětí, které se projevuje disipací (rozptylem) kinetické energie. V některých textech je toto obrazně popisováno jako „vnitřní tření“ v kapalině. Fyzikální veličinou, která charakterizuje vnitřní napětí v kapalině, je viskozita. Dynamická viskozita (η) je definována jako koeficient úměrnosti mezi smykovým napětím dvou sousedních vrstev proudící kapaliny a gradientem rychlosti mezi těmito vrstvami:

Pro potřeby fyzikální a technické praxe se zavádí ještě kinematická viskozita (ν), která je definována jako dynamická viskozita dělená hustotou kapaliny (4).

Pokud je dynamická viskozita nezávislá na smykovém napětí resp. na rychlosti proudící kapaliny, hovoříme o newtonovských kapalinách. Tyto kapaliny se chovají očekávaným způsobem a matematická analýza jejich proudění je mnohem snazší. V řadě významných případů ovšem dynamická viskozita závisí na rychlosti proudění kapaliny, kterou pak nazýváme „nenewtonovská“ neboli „nelineárně viskózní kapalina“ a která se chová v některých ohledech neočekávaně. Matematický popis jejího proudění je pak pochopitelně mnohem obtížnější (5).

Další významnou fyzikální vlastností kapalin je povrchové napětí. Povrchové napětí je makroskopický projev mikroskopických kohezních sil, kterými se molekuly kapaliny navzájem přitahují. Na molekulu nacházející se na hranici (hladině) působí síly, které vtahují molekulu zpět do kapaliny. To znamená, že na přemístění molekuly k hladině je třeba vykonat určitou práci a tedy molekuly těsně při hladině mají vyšší potenciální energii než molekuly uvnitř kapaliny. Povrchové napětí je vlastně mírou toho, o kolik je vyšší vnitřní energie molekul na hladině ve srovnání s molekulami v hloubce kapaliny. Protože termodynamický systém má tendenci zaujímat stav s minimem energie, dochází k tomu, že se spontánně zmenšuje povrch kapaliny – např. kapka bez působení vnějších sil zaujme tvar koule. Makroskopicky se existence kohezních sil projevuje tak, jako kdyby byla hladina kapaliny pokryta tenkou pružnou blánou (6).

Fyzikální vlastnosti krve

Z hlediska fyziky kapalin má krev řadu výrazně neideálních vlastností. Tekuté prostředí krve, krevní plazma, je roztok solí, malých organických sloučenin a proteinů, ve kterém jsou dispergovány formované krevní elementy. Toto specifické složení se projevuje tak, že krev je výrazně nenewtonovská kapalina. Nenewtonovský charakter krve je méně vyjádřen pro vyšší hodnoty smykového napětí, tedy pro vyšší rychlosti jejího proudění (5).

Z formovaných krevních elementů mají na fyzikální vlastnosti krve vliv především erytrocyty. Zatímco běžné suspenze uvažované v technické praxi mají takové vlastnosti, že dispergované částice lze pokládat za pevné, erytrocyty mohou i za fyziologických podmínek poměrně snadno reverzibilně měnit svůj tvar. Krev tak může být modelována jako suspenze typu pevná látka v kapalině, realističtější výsledky ovšem dává modelování erytrocytů jako nesplývajících kapek nerozpustné kapaliny. Chování erytrocytů komplikuje hemodynamiku ještě dalším způsobem: Erytrocyty vykazují tendenci k vytváření lineárních agregátů (rouleaux), které mohou dále interagovat a vytvářet trojrozměrné struktury. Rouleaux a tím spíše i vyšší struktury erytrocytů se snadno rozpadají v krevním toku, tendence k jejich vzniku převažuje v netekoucí krvi. Vznik těchto struktur je ovlivněn řadou faktorů, klinicky se hodnotí jako krevní sedimentace. V případě krve ex vivo se mohou tyto struktury podílet na výrazné závislosti viskozity na deformaci krevní kapky při malých deformačních rychlostech (7). Významnou roli v procesech ovlivňujících chování krve ex vivo hrají faktory podílející se na krevní koagulaci. Časový horizont formování krevních stříkanců je ovšem natolik krátký, že tyto faktory vlastní aktivací významnějším způsobem nezasahují do dějů podílejících se na vzniku, letu a dopadu krevní kapky, mohou se ale uplatnit u následujících procesů spojených se změnami v krevním stříkanci krátce po dopadu na podložku. Následný proces zasychání krve také může poněkud změnit charakter krevního stříkance (8).

Při různých hematologických onemocněních se mohou reologické vlastnosti krve měnit. Skutečně dramatické změny viskozity krve lze pozorovat například při makroglobulinémii, podobně lze pozorovat změny viskozity například při deficitu fibrinogenu nebo při anémii (5). Některé jiné patologické stavy, například ikterus, ovlivňují i povrchové napětí krve (8). Přitom tyto dva fyzikální parametry mohou ovlivnit procesy probíhající při formování, letu i dopadu krevní kapky.

Jen pro úplnost zmiňujeme to, že precizní fyzikální analýza chování krve jako kapaliny založená na rozboru všech podstatných a potenciálně zajímavých fyzikálních a fyzikálně chemických vztahů v krvi jako v nehomogenním systému vede k poměrně složitým vztahům řešitelným obvykle jen numericky (10). Takový detailní model fyzikálních vlastností krve je užitečný třeba pro studium fyziologických a patofyziologických procesů souvisejících s tokem krve.

Zásadní nevýhodou podrobných modelů je vyšší počet vstupních parametrů, které je třeba stanovit. To limituje využití takových modelů v BPA, protože v praxi často nebývá možné stanovit všechny parametry modelu. To poukazuje na jednu vlastnost zejména aplikované fyziky, která bývá někdy opomíjena: Pro jeden děj lze použít několik různě detailních modelů podle toho, jak velká nejistota je při řešení dané úlohy přijatelná. Na jedné straně velmi jednoduchý model může mít hodnotu pouze didaktickou, s rostoucí složitostí modelu roste i jeho schopnost přesněji předvídat výsledky experimentu, ale obvykle klesá jeho použitelnost pro výpočetní náročnost a pro nutnost určení většího počtu vstupních parametrů. Na druhou stranu, zvyšování složitosti modelu nemusí nutně vést k přesnějším výsledkům. V praxi se obvykle postupuje tak, že se volí co nejjednodušší model, který v rámci vymezeného pole působnosti dává ještě dostatečně dobré výsledky.

Výše naznačený přístup je obvyklý i v biologii a medicíně – tak například řada úvah normální a patologické fyziologie krevního oběhu vychází z předpokladu, že krev je newtonovská kapalina. Navzdory značnému zjednodušení jsou výsledky takových úvah obvykle dost dobré na to, aby byly aplikovány v klinické praxi.

LET KAPKY KRVE

V prvním fyzikálně korektním přiblížení lze letící kapku modelovat hmotným bodem pohybujícím se v homogenním gravitačním poli bez patrného odporu prostředí. Řešením pohybové rovnice je parabola (4). V některých situacích může být zakřivení paraboly na uvažovaném měřítku tak malé, že lze dráhu aproximovat přímkou. Cenou za podstatné usnadnění výpočtu je v takovém případě nepřesnost, která může být při malých vzdálenostech od PO a při vyšších rychlostech letu krevní kapky poměrně malá (viz obrázek 1). Rovněž je třeba brát v potaz viskozitu vzduchu a při sestavování pohybové rovnice se tedy objevuje další člen. Se zohledňováním dalších faktorů tak trajektorii nejlépe popisuje balistická křivka. V řadě teoretických publikací (i v praxi) je preferována aproximace letu kapky přímkou (11-13), protože jde o zdaleka nejjednodušší přístup.

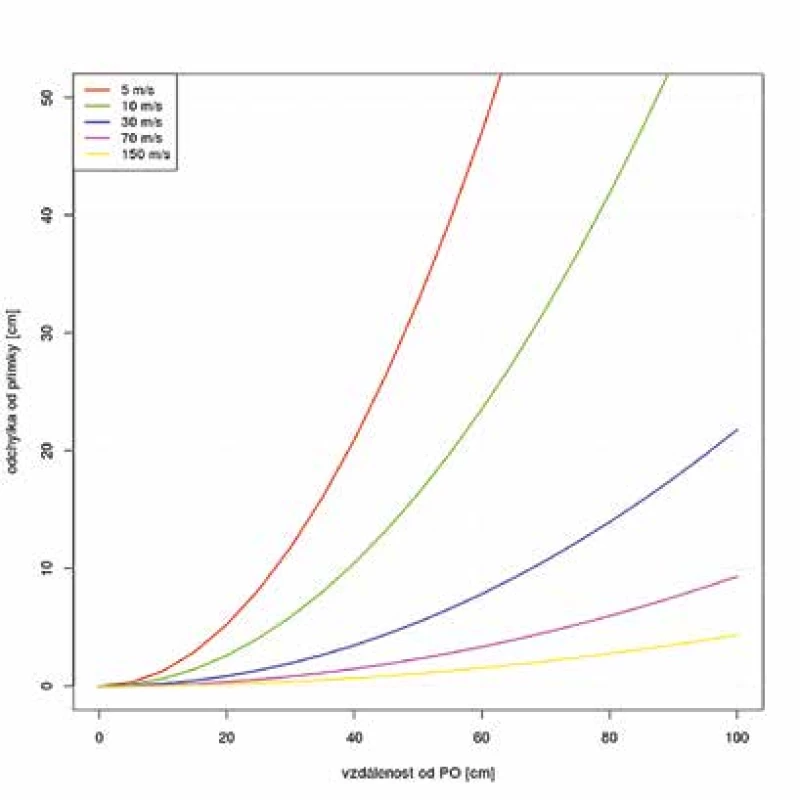
Z jednoduchého fyzikálního náhledu je zřejmé, že aproximace balistické křivky přímkou může být dostatečně přesná jen na poměrně krátké dráze a jen v určitém pásmu rychlostí. Pokud poletí krevní stříkanec příliš pomalu, bude zakřivení dráhy vlivem gravitačního pole významné. Pokud naopak bude rychlost letu krevní kapky příliš vysoká, významnou měrou se uplatní odpor vzduchu a další jevy ve vlastní kapce. Podle míry vlivu gravitace, prostředí a procesů v kapce tak může jednoduchý odhad pomocí přímky výrazně nadhodnotit i podhodnotit odhad výšky, ve které krevní kapka vznikla (13). Ukazuje se, že na přesnost odhadu má vliv i velikost kapky v tom smyslu, že malé kapky se více odchylují od předpokládané přímkové trajektorie (14).

Popis trajektorie letu kapky krve pomocí balistické křivky má pro praktické využití jednu podstatnou nevýhodu: Zatímco při popisu trajektorie pomocí přímky lze zanedbat počáteční rychlost a tvar kapky, v případě popisu pomocí balistické křivky hraje počáteční rychlost klíčovou roli, stejně jako hmotnost (velikost) kapky. V případě, že jsou uvažovány další vlivy, je třeba do popisu zahrnout i tyto. Sice bylo publikováno několik prací zabývajících se kvantitativním odhadem rychlosti dopadající kapky krve z morfologie výsledného obrazce, ale výsledky nejsou příliš povzbudivé (12).

Precizní model letící kapky krve jako komplexního fyzikálního systému, např. takový, jaký popisují Kabaliuk a kol. (12), umožňuje studovat předpokládané chování krevních stříkanců. Větší počet vstupních parametrů a komplikovanější matematické vyjádření jsou však často limitujícím faktorem pro obvyklou úlohu, tedy nalezení bodu v prostoru, ze kterého krevní stříkance vycházely. Takovýto model však může dát mnohem spolehlivější odpověď na otázky typu kam až mohly krevní kapky dolétnout za předpokládaného průběhu úrazového děje apod. Podobě jako v jiných oblastech lidské činnosti i zde platí, že volba vhodného modelu je úkolem experta v příslušné oblasti.

DOPAD KAPKY KAPALINY

Formování stříkance běžné kapaliny

Dopad kapky kapaliny na pevný povrch je běžný děj. Detailní studium chování dopadající kapky odhaluje, že i v případě kolmého dopadu kapky newtonovské kapaliny na homogenní povrch může nastat řada situací. Je popisováno šest morfologických typů dopadu kapky: depozice (deposition), okamžité rozstříknutí (prompt splash), koronové rozstříknutí (corona splash), postupný rozpad (receding break-up), částečný odraz (partial rebound) a úplný odraz (complete rebound). Pro posouzení toho, k jakému fenoménu dojde, se u newtonovských kapalin používají tři parametry: Reynoldsovo číslo, Weberovo číslo a smáčivost povrchu příslušnou kapalinou. Podobnostní čísla v sobě zahrnují velikost a rychlost kapky a hustotu, povrchové napětí a viskozitu kapaliny. Pro chování dopadající kapky jsou významné i vlastnosti dopadové plochy. Sklon a vyšší teplota zvyšují pravděpodobnost, že dojde k odrazu. Drsnost povrchu zřejmě souvisí s tím, že se kapka rozstříkne zřetelně nesymetricky, roztříštěná kapka dává vzniknout řadě sekundárních kapek. Zdrojem asymetrií mohou být i vzduchové bubliny zachycené dopadající kapkou (16).

Morfologii dopadového modelu komplikují další faktory na straně kapky i dopadové plochy. Kapka může oscilovat mezi tvarem koule a elipsoidu (16). Nezanedbatelná viskozita vzduchu při letu kapky vede k dalším deformacím tvaru od ideální koule (17). Podle mechanismu vzniku a doby letu může mít kapka i vlastní nezanedbatelnou rotaci a takto přenášený moment setrvačnosti pak může ovlivnit jak tvar letící kapky, tak i charakter roztékání kapky po dopadové ploše.

Pro praktické úvahy je podstatné, že výsledný tvar krevní stopy výrazně ovlivňuje zvlnění povrchu dopadové plochy s jasně převažujícím směrem. Situace není vůbec jednoduchá, v závislosti na podmínkách se může dopadající kapka kapaliny šířit více směrem podél zvlnění i směrem kolmým ke zvlnění povrchu dopadové plochy (18).

Bylo studováno taktéž chování kapek dopadajících na povrch, který není směru letu kapky postaven kolmo. Pro velké hodnoty Weberova čísla, tedy např. pro vysoké hodnoty rychlosti letu kapky, se dopad kapky odlišuje od dopadu na rovnou plochu především ve smyslu rozsahu a symetrie šíření kapaliny (19,20).

Pokud nedopadá čistá kapalina ale suspenze s vysokým podílem suspendovaných částic, chování dopadající kapky se změní, spíše kvantitativně než kvalitativně. Pohotovost k rozstříknutí kapky suspenze je obvykle vyšší ve srovnání s pohotovostí k rozstříknutí čistého disperzního prostředí, bylo však pozorováno i opačné chování. Změny při dopadu mohou vést k tomu, že se suspendované částice ve výsledném otisku rozptýlí nehomogenním způsobem, např. mohou vytvářet shluky. Dopadající kapka suspenze tedy vykazuje jisté odlišnosti v chování ve srovnání s dopadem čisté kapaliny (21). Tento fakt komplikuje přenášení poznatků získaných při studiu čistých kapalin na suspenze.

Formování krevních stříkanců

Protože se krev jako kapalina chová mnohem komplexněji než výše uvedené čisté kapaliny nebo suspenze typu pevná látka v kapalině, lze očekávat, že chování krve se bude lišit od chování těchto modelů. V případě dopadu kapky krve lze její chování po dopadu také odhadnout pomocí Reynoldsova a Weberova čísla, vliv mají opět také vlastnosti povrchu dopadové plochy. Okraj krevního stříkance není hladký, je zvlněný drobnými záhyby (scallop) nebo štíhlými až trnovitými výběžky (spike). V několika studiích bylo demonstrováno, že počet těchto výběžků je úměrný podobnostním číslům, v nejjednodušší podobě druhé odmocnině Weberova čísla (22). Protože samo Weberovo číslo je závislé na rychlosti pohybující se kapky, je počet těchto výběžků úměrný dopadové rychlosti kapky. Z fyzikálního hlediska je významné, že nejde jen o hledání korelací, ale že lze analyzovat procesy, které za tímto jevem stojí. Undulace okraje krevního stříkance je přímým důsledkem srážky kapky s podložkou. Dopad kapky na plochu vyvolá vlny v obecném slova smyslu, které se dynamicky šíří kapkou (16,22). Pro praktické potřeby se však ukazuje, že odhad rychlosti dopadající kapky je jen velmi rámcový a jeho užitečnost je tedy značně limitovaná (14).

Z praktického hlediska má mnohem větší význam dopad kapky na plochu, která není kolmá k letu kapky. Predominantní tvar takové kapky je zhruba eliptický. Modelování tvaru stříkance elipsou (ellipse fitting,) umožňuje snadný odhad dopadového úhlu. Předpokládá se, že dopadový úhel α stříkance je možné odhadnout z šířky (W) a délky (L) elipsy nejlépe ohraničující krevní stříkanec (2):

Tento vztah se někdy označuje jako „sinový zákon“. Jeho geometrická interpretace je přímočará. Předpokládá se, že letící krevní kapka je koule a trajektorie svírá v okamžiku dopadu s rovinou dopadu úhel α. Směr trajektorie v okamžiku dopadu se stane osou pomyslného válce těsně obalujícího kapku krve a průsečík válce s rovinou dopadu vymezí elipsu. Předpoklad je, že tato elipsa bude mít délky poloos právě W a L, kde W bude současně průměr dopadající kapky.

Navzdory silnému označení „sinový zákon“ pokládá např. Adam (22) za překvapující, jak málo pozornosti bylo věnováno experimentálnímu ověření tohoto vztahu. Joris a kol. (24) poukazují na to, že tento přístup, ačkoliv je dominantní, zcela ignoruje drtivou většinu faktorů podílejících se na formování stříkance. Ve své práci použili odlišný přístup. Vůbec se nesnažili sestavit fyzikální model, který by popisoval procesy spojené se vznikem, letem a dopadem krevní kapky. V potaz vzali pouze to, že fyzikálně je možné, že tvar krevního stříkance v sobě nese informaci o úhlu, pod kterým krevní kapka dopadla na podložku. S využitím metod zpracování obrazu a samoučících se algoritmů sestrojili klasifikátor, který byl schopný na základě tvaru stříkance stanovit pravděpodobný úhel dopadu. Takto sestavený klasifikátor byl v experimentu úspěšný, jeho výsledky byly vesměs přesnější než odhad úhlu dopadu založený na modelování stříkance elipsou. Zde je zajímavé, že automatické modelování krevního stříkance elipsou, tedy vlastně fitování obrazce, vedlo i tak k lepším výsledkům než manuální určení vhodné elipsy. Je třeba zdůraznit, i když to autoři nezmiňují, že relativní chyba všech metod pro malé dopadové úhly přesahuje hodnotu 10 % a s rostoucím dopadovým úhlem klesá (23). Z toho hlediska není překvapující ani zdánlivě kontradiktorní teoretická závislost šířky stříkance na čtvrté odmocnině sinu dopadového úhlu (22).

NEJISTOTA ODHADU PO

Letící kapka krve i formující se krevní stříkanec podléhají řadě vlivů. Často jde o vlivy nepodchytitelné nebo jen velmi obtížně podchytitelné, tedy vlivy, které lze považovat za náhodné. Některé z těchto chyb, či spíše nejistot, vycházejí z odchylek použitých modelů od reálného chování krve. Z toho důvodu je možné očekávat, že odhad PO z jednoho stříkance je zatížen téměř znehodnocující nejistotou. Řada autorů předpokládá, že poruchové vlivy lze matematicky modelovat jako obvyklou chybu měření resp. nejistotu měření, tedy jako aditivní náhodnou veličinu s nulovou střední hodnotou (12). Takové chyby lze výrazně eliminovat tím, že se provede odhad PO z většího počtu krevních stříkanců a výsledný odhad PO se vypočítá jako průměrná hodnota jednotlivých odhadů. Po doplnění odhadu nejistoty např. pomocí směrodatných odchylek lze tak vymezit oblast v prostoru, ze které se analyzované kapky s největší pravděpodobností rozlétly. Odhad lze dále zpřesnit technikou, která je ve statistice poměrně běžná, totiž vyloučením odlehlých hodnot (12). Podstatou zpřesnění při tomto postupu je předpoklad, že odlehlá hodnota je s větší pravděpodobností zatížena větší náhodnou chybou. Protože je výpočet aritmetického průměru na odlehlé hodnoty citlivý, předpokládá se, že jejich vyloučením bude průměr lepším odhadem správné hodnoty, tedy zde lepším odhadem příslušné souřadnice PO. Vylučování odlehlých hodnot by nemělo obecně probíhat prostým odhadem, vlastní provedení je popsáno v každé učebnici fyzikálního nebo technického měření. Jde o iterativní postup, při kterém se postupně ze souboru vylučují ty hodnoty, které leží mimo definované pásmo odlehlých hodnot. Podobně jako u řady dalších metod úpravy dat hrozí, že při nevhodném použití dojde ke zkreslení výsledku a místo požadovanému zpřesnění odhadu PO dojde ke znehodnocení odhadu.

Při práci s nejistotou jde zajít ještě dál než jen k předpokladu, že nejistota určení PO se chová podobně jako většina nejistot měření. Například Camana (23) přistupuje k této problematice tak, že se pokouší metodami teorie pravděpodobnosti modelovat pravděpodobnostní chování poruch exaktněji. Výsledkem jeho práce je popis statistického chování nejistot určení PO, který lze použít k lepšímu odhadu PO. Cenou za to je méně obvyklý popis, který může komplikovat mechanické použití takového přístupu v praxi.

Z hlediska kvality výsledného odhadu PO je podstatný v neposlední řadě také výběr krevních stříkanců, které budou použity k další analýze. Vhodným výběrem lze odhad zpřesnit, nevhodný výběr naopak výsledek znehodnocuje. De Bruin a kol. (15) studovali přesnost odhadu místa původu krevního stříkance v závislosti na charakteru stříkance. Výsledkem jejich práce je doporučení, že k analýze by měly být vybírány stříkance splňující následující tři podmínky:

1. leží blízko předpokládaného místa původu,
2. jsou větší než 1,5 mm,
3.  jejich tvar je eliptický.

V této souvislosti stojí za zmínku přístup, který popisují Buck a kol. (25). Krevní stříkance, které se nacházejí v blízkosti předpokládaného místa vzniku, analyzují pomocí aproximace dráhy letu krevní kapky přímkou. Vzdálenější stříkance analyzují pomocí prostředků balistiky. Bohužel autoři nezmiňují detaily jimi provedené balistické analýzy a z publikace tedy není jasné, jaké předpoklady použili k tomu, aby mohli získat pravděpodobný průběh balistické křivky.

ZÁVĚR

Určení místa vzniku krevních stříkanců je zajímavá oblast na pomezí soudního lékařství a fyziky, zejména biomechaniky. Pro praktické využití jsou však let kapky krve i formování krevního stříkance značně složité fyzikální procesy ovlivněné celou řadou obtížně podchytitelných faktorů. Z toho důvodu je třeba přistupovat k určení místa vzniku krevních kapek velmi obezřetně. Důležitý je výběr vhodných kapek k další analýze a volba vhodné metody pro odhad PO, která by měla zahrnovat také statistickou analýzu výsledku. Pro interpretaci výsledku je třeba mít vždy na paměti, že v procesu analýzy byla významně zjednodušena fyzikální skutečnost, takže stanovená hodnota je z principu zatížena nejistotou. Nelze tedy bezpečně tvrdit více než to, že zdroj krevního stříkance se nacházel v jisté velmi malé oblasti prostoru, je třeba připustit nejistotu. Bez respektu k fyzikálním omezením by se mohlo stát, že časem bude celá oblast analýzy krevních stříkanců zpochybněna jako „junk science“ (26).

PROHLÁŠENÍ

Autor práce prohlašuje, že v souvislosti s tématem, vznikem a publikací tohoto článku není ve střetu zájmů a vznik ani publikace článku nebyly podpořeny žádnou farmaceutickou firmou. Toto prohlášení se týká i všech spoluautorů.

∗ Adresa pro korespondenci:

MUDr. Jaromír Šrámek

Ústav histologie a embryologie 1. LF UK

Albertov 4, 128 00 Praha 2

tel.: +420 224 968 118

fax: +420 224 919 899

e-mail: jsram@lf1.cuni.c