MODELING OF THE CHEMICAL STAGE OF RADIOBIOLOGICAL MECHANISM USING PETRI NETS

Summary

The biological effect of ionizing particles is caused mainly by water radicals being formed by densely ionizing ends of primary or secondary charged particles during physical stage; only greater radical clusters being efficient in DNA molecule damaging. The given clusters diffuse after their formation and the radical concentration changes also by reactions running mutually or with other substances being present in corresponding clusters. The damage effect depends then on radical concentrations at a time when the cluster meets a DNA molecule. The influence of oxygen may be important (mainly in the case of low-LET radiation) because oxygen is always present in living cells. Oxygen may act then in two different directions: at small concentrations the interaction with hydrogen radicals prevails and final biological effect diminishes while at higher concentrations additional efficient oxygen radicals may be formed. The time evolution of changing radical concentrations during cluster diffusion may be modeled and analyzed well with the help of Continuous Petri nets.

Keywords:
Radiobiological mechanism, chemical phase, DSB formation, Petri nets

Introduction

The radiobiological effect of ionizing particles consists in principle always of three stages; physical, chemical and biological. The biologically efficient damage of DNA molecules may be then given by radicals formed in clusters by densely ionizing track ends of individual ionizing particles. Before meeting a DNA molecule these radicals react mutually or with some other species being present in corresponding water medium; the number of efficient radicals may be lowered or heightened by these additional reactions. Direct effect caused by primary or secondary charged particles may be practically neglected; especially for radiation of lower LET.

However, the efficient damage (i.e., a DSB) may occur only in a short time after cluster formation when radical concentration (diminishing with cluster diffusion) is sufficiently high as at least two SSBs must be formed in close neighborhood. This efficiency of individual radicals is then influenced by chemical processes running in corresponding clusters as well as by lowering of non-homogeneous concentrations during radical cluster diffusion.

We proposed already earlier the mathematical model making it possible to describe the combined effect of these two processes [3, 6]. Recently the given model has been extended by including Petri nets [7], which has made it possible to describe easily the time evolution of radical numbers in corresponding clusters, too. The model has been applied to experimental data of the yields of individual radicals in anoxic water radiolysis at the instant of cluster formation and at the end of its diffusion; good agreement having been obtained.

However, the living cells contain usually an amount of oxygen molecules that influence significantly final biological effect. In this paper we shall show how the presence of oxygen molecules contributes to increasing number of radicals efficient in damaging DNA molecules. In the given process the cluster of radicals e^-_aq, H•, OH•, H₃O⁺ (formed at the end of physical stage) take part. The initial yields of these primary radicals may be taken from the literature; their estimates in the dependence on energy transfer are included in the most compilations concerning the radiation chemistry of water (see e.g. [9, 11, 12, 16, 17, 18, 20, 21, 26, 27, 28]). However, the participation of associated products (OH•, H_2, H₂O₂, O₂^-, HO₂^•, O₂ ) is to be taken into account, too.

For low-LET radiation the size of radical clusters depends practically on the energy distribution of secondary electrons. Mozunder and Magee [19] has divided the corresponding clusters according to transferred energy into three groups: (1) spurs (spherical entities, up to 100 eV); (2) blobs (spherical or ellipsoidal, 100-500 eV); (3) short tracks (cylindrical, 500-5000 eV). Our considerations will concern in principle two smaller cluster types.

In the following the clusters (at low-LET radiation) will be described (for simplicity) as spherically symmetric systems. Two main parallel processes will be assumed to be running in any cluster: chemical reactions of radicals formed at energy transfer and contemporary cluster diffusion. The dynamics of chemical reactions depends then on cluster diffusion due to concentration changes of corresponding chemical species.

As already mentioned we have started to study the corresponding problem earlier, the contemporary result of chemical reactions and cluster diffusion having been described with the help of corresponding differential equations; our model has been applied to the experimental data obtained for Co60 radiation [3, 4, 5, 6]. The average excitation energy of efficient clusters should be approximately 300 eV (estimated according to results obtained in radiation chemistry studies). In [7, 8] Continuous Petri nets have been then used to simulate time dynamics of chemical stage under anoxic conditions. The changes in efficiency of corresponding individual clusters in dependence on their sizes (in anoxic water) have been studied. In the following we shall show the influence of oxygen on the dynamics of the chemical stage. More detailed analysis might help in understanding better the so called oxygen effect that may play important role in tumour radiotherapy.

Mathematical model including oxygen influence

The corresponding mathematical model of chemical stage starts from the assumption that the given process (damaging DNA molecule) is mediated by diffusing radical clusters containing non homogeneous concentrations of individual species [21, 23]. Macroscopic laws have been then used to describe the diffusion of radiation-induced objects and concentration changes caused by different chemical reactions. Recently we have extended the given model by adding Continuous Petri Nets, which has enabled us not only to follow the changing radical concentrations during cluster diffusion but also to define easier the system of corresponding basic differential equations. The model has been based on the basic assumption that the cluster diffusion has been determined by diffusion coefficients of corresponding radicals and the numbers of these radicals has been changing during this diffusion by chemical reactions running inside any cluster. The beginning of the given process has been given by the volume V_i (t=0) = V₀ of the cluster and by the numbers of corresponding radicals N_i (t=0).

It has been then possible to define the concentrations of individual radicals

and to express the corresponding derivatives as common effect of cluster diffusion and chemical reactions running in the cluster

Using Eq. (1) one may rewrite Eq. (2) as

The diffusion change of average volumes of individual radicals has been then derived as sphere symmetrical diffusion starting from the center of corresponding cluster:

where t₀ corresponds to the theoretical time period between the cluster origin in its center and volume representing the starting size of corresponding radical cluster.

The system of ordinary differential equations can be solved numerically using standard procedure, where the Continuous Petri nets may be very helpful. Great advantage of Petri nets for modeling complicated distributed systems consists in the possibility of being easily created with the help of graphical tools and of rapid analysis of the corresponding system, which enables us to optimize the parameters of a mathematical model [14, 15, 24, 25]. Unlike classical methods the Petri nets enable us to form gradually a mathematical model via places and transitions. The model may be tested, easily expanded and improved at each stage. The detailed description of our model including Petri nets and corresponding mathematical definitions may be found in [7, 8]. Here only main points and formulas will be introduced.

Continuous Petri nets consist of three main elements: places, transitions and arcs. The places represent the state of the system; see Fig. 1. Each place is marked by a real number, which determines the amount (value) of monitored parameter (e.g., the concentration of a chemical substance in a volume, etc.). The real number determining the state of a monitored place, can be changed via transition. The dynamic change of a place is given by corresponding transitions determined with the help of differential equations. Each place can be changed only via the transitions which are linked to it.

The dynamic changes of all places caused by the corresponding transitions occur simultaneously. It is the process similar to solving a system of differential equations with the difference that here we do not have anything complicated to program and debug.

The clusters arising by energy transfer have given sizes and are formed by given numbers of radicals and some other species and by some average volume, which may be characterized by values N_i (0) and Vj (0) = Ṽ, where the numbers of individual chemical species have been taken from already published data (under corresponding conditions) and quantities Ṽ and t₀ (see Eq. (4)) have been established by fitting corresponding experimental data [6]. These values of N_i (0) and V_j (0) represent then actual initial values of the cluster evolution described by Eqs. (3) and (4).

Individual places and transitions are entered graphically and then joined using the arcs. The right side of the differential equation for each transition is given by a simple term. The simulation model is created by adding gradually places and transitions, and each step can be tested. Complex model with a large number of places and transitions can be very quickly created. The model allows rapid analysis when different free parameters are to be optimized according to corresponding data.

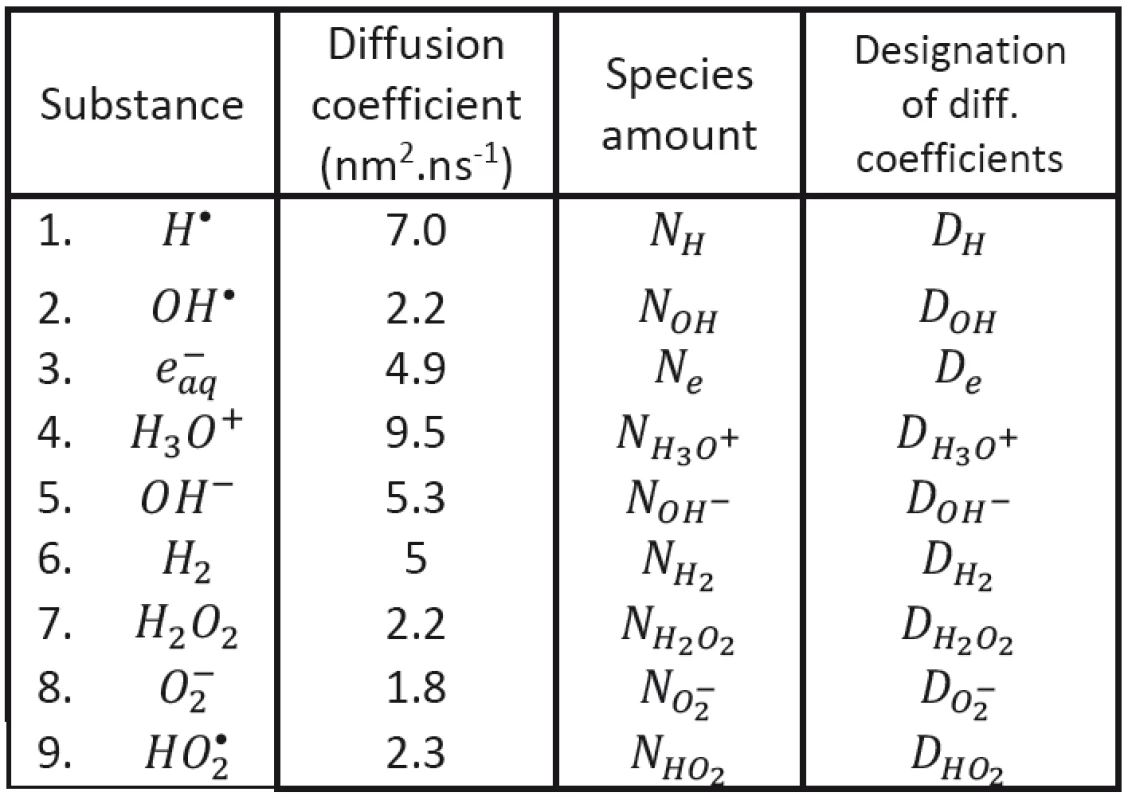
We shall assume that the radicals shown in Tab. 1 may be involved in processes responsible for radiobiological effect; their diffusion coefficients taken from the literature having been introduced, too. As to the content of radicals in the clusters at (at the beginning of cluster diffusion) we shall assume that only the following species will be present: H•, OH•, e^-_aq, H₃O⁺, H₂ and . Considered chemical reactions are then introduced in Tab. 2; the reaction rates (taken from the literature in corresponding units) are also given in this table [12, 13].

We have used the system Visual object net ++ [22] to create the given mathematical model characterizing the evolution of corresponding cluster after its formation with the help of Continuous Petri nets. In this tool the transition functions may be included as well as the places that are not joined with it. It enables us to create simpler graphical simulation model.

The whole process dynamics is expressed graphically by continuous Petri nets in Fig. 1, where the places are marked as H, OH, e, H3O, OHM, H2, H2O2, O2M, HO2 (representing individual species contained in Tab. 1) and as O2. Other places correspond then to average volumes of individual radicals, to rates of chemical reactions, diffusion coefficients and also to value of used in corresponding expressions.

A value is assigned to each place; it represents the amount of corresponding species. Individual places may be changed via corresponding transitions. Each transition represents the change rate of species number due to chemical reaction introduced in Tab. 2. All places and transitions are shown in Fig. 1. The places which are at the top represent constants from tables 1 and 2 (diffusion coefficients and chemical rate values). The places at the left of Fig. 1 represent volumes of corresponding particles, increasing during cluster diffusion. Their changes take place through the connected transitions. Other places which represent the amounts of individual species are changed due to transitions that are connected with them. In Fig. 1 we also may see how chemical reactions take place.

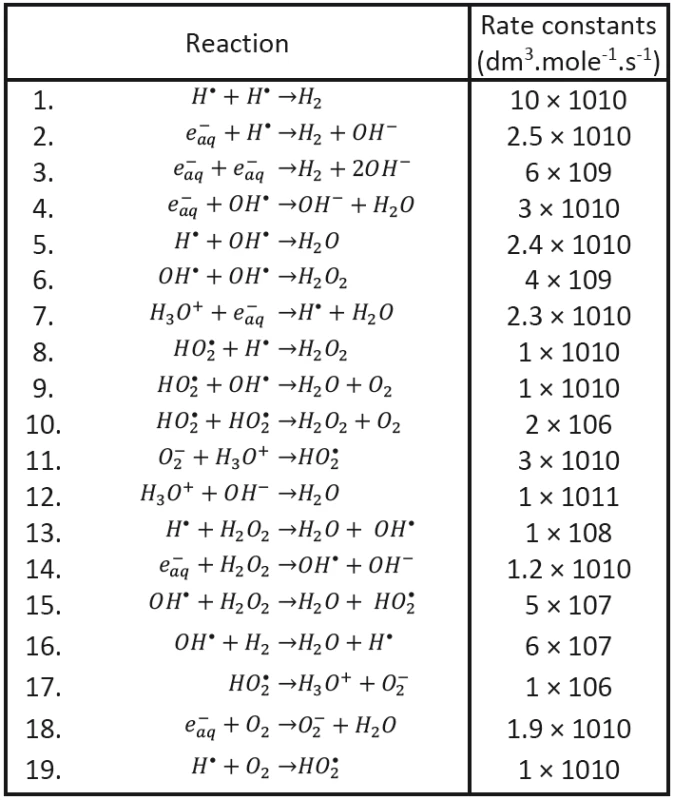
The whole process can be described by the following system of ordinary differential equations, which includes the influence of chemical reactions and diffusion of radicals simultaneously:

Volume transitions corresponding to changes caused by diffusion will be given by a system of ordinary differential equations

where X represents corresponding radical or species forming the diffusing cluster; in the system of differential equations (15) it will be replaced subsequently by H, OH, e, H₃O⁺, OH^- , H₂, H₂O₂, O₂^- and HO₂. At to the difference to Eq. (4) the parameter t-zero is not needed in Eq. (15) if V_j(0) is defined by V_o.

All chemical reactions run in parallel according to equations (5-14). Concurrently with chemical reactions the volume of radical cluster increases according to Eq. (15) due to diffusion into surrounding. The individual terms on the right-hand side of ordinary differential equations are then given in Petri nets by the following transitions.

Transitions (16) cause changes of species numbers. The transitions causing the changes of cluster volumes of corresponding radicals may be expressed in the case of spherical symmetry in the form

where X represents again corresponding species H, OH, e, H3O⁺, OH^- , H₂, H₂O₂, O₂^- and HO₂.

The graphical representation of preceding mathematical expressions may be seen in Fig. 1. The graphical model is practically clear and may be simply compiled, which allows us to solve very complex systems considered in radiobiology. One can also easily include mutual chemical reactions of species present in the cluster. The model simulation using Continuous Petri nets is very fast, which allows us to study the influence of individual model characteristics.

The evolution of clusters characterized by initial conditions is then determined by diffusion coefficients D_H, D_OH, D_e, D_H3O+, D_OH-, D_H2, _H2O2, D_O2-, D_HO2 and by rate constants κ1 - κ19 established on the basis of earlier experimental data and taken from the literature (see Tab. 1 and Tab. 2). The proper initial conditions (volume and the numbers of corresponding species) will be then determined by transferred energy; their values (or rather their ratios) established in literature for a given kind of ionizing particles having been respected. All these conditions should be, of course, still further tested.

If oxygen is present then it is necessary to mention the emergence of HO₂ radicals. They may arise due to energy transfer inside the cluster by the reaction

minimum electron energy ~ 4 eV, maximum gain at 8 eV. A part of these radicals react in water medium and new radicals are formed:

Number of radicals in the cluster depends on oxygen concentration in solution. It means that all initial conditions of individual radical clusters will be the same as in anoxic case, radicals will be formed in reactions running in clusters.

Petri nets model and experimental data

The suggested mathematical approach enables us to describe time evolution of processes running in individual radical clusters during the chemical stage of water radiolysis in dependence on oxygen concentration.

Assuming the spherical symmetry of corresponding clusters and knowing the diffusion coefficients of individual species (see Tab. 1), we have derived already earlier that the cluster evolution may be characterized by parameter representing the time having passed from the instant of theoretical diffusion center point origin. It has been then derived with the help of mentioned optimization approach that the average initial size of efficient clusters (formed by Co60 radiation has been cca 27 nm, which has corresponded to the value t₀ = 13 nsec (equal to time interval needed for cluster evolution from the theoretical center point.

To demonstrate possible advantage of the new approach (using Petri nets) we shall start with comparing our results with experimental data established for initial and final characteristics of corresponding clusters in the case of Co60 radiation applied to deoxygenated water system [12, 18]. Initial clusters (consisting of radicals H•, OH•, e^-_aq, H₃O⁺ and H₂) may be characterized by radical yield values G⁰ immediately at the end of physically-chemical stage; the values corresponding to cluster energy of 100 eV have been established: N_H = 0,42, N_OH = 5,5, N_e = 4,78, N_H3O+ = 4,78, N_H2 = 0,15.

With the help of Petri nets it has been then possible to determine the time evolution of individual radicals in individual clusters (see Fig. 2). The values obtained in the end of the corresponding chemical stage (after cluster diffusion) may be compared to the yield values of established experimentally; evidently very good agreement having been obtained; see Tab. 3.

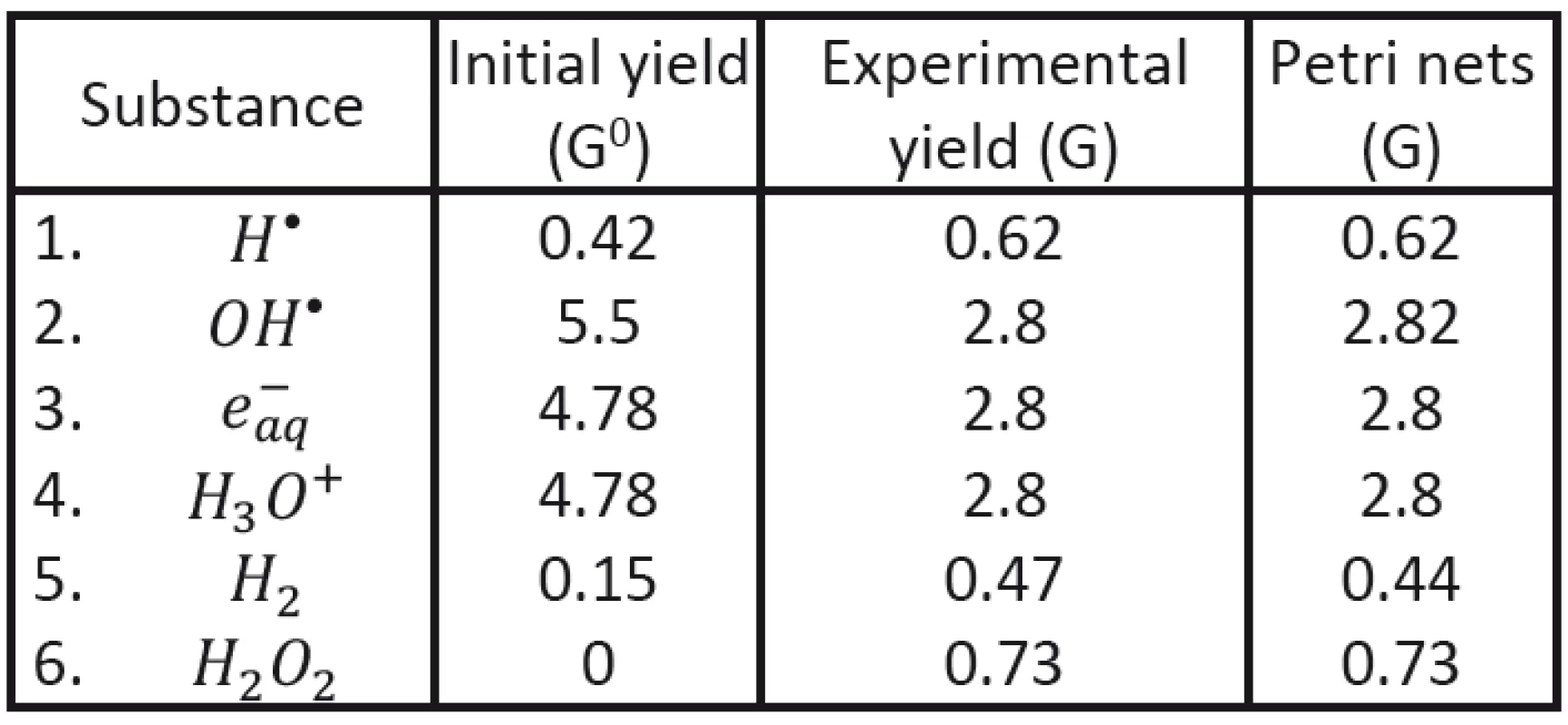
Our further results will concern the results obtained for average efficient clusters formed by Co60 radiation on the basis of experimental data presented by Blok and Loman 1973 [10] (see [6]). Initial size of clusters efficient in DSB formation has corresponded to energy 300 eV and its volume diameter has been cca 27 nm, which has corresponded to the value t₀ = 13 nsec in spherical approximation. It means that all radicals will be contained practically in the volume where ns.

Initial number of radicals N_H, N_OH, N_e, N_H3O+, N_OH-, N_H2, N_H2O2, N_O2-, N_HO2 will then correspond to the yield G⁰ established under anoxic conditions for transferred energy 300eV [12, 18]. It will be put ; ; =14.34; while initial numbers of other radicals , will be equal to zero. Using the values of diffusion coefficients D_H, D_OH, D_e, D_H3O+, D_OH-, D_H2, D_H2O2, D_O2-, D_HO2 and of rate constants k₁ − k₁₉ (see Tab.1 and Tab. 2) the time dependences of corresponding radical numbers may be derived with the help of Fig. 1 and equations (5)-(35). In the following we shall show, however, rather the time dependencies of individual radical concentration, s as they are more suitable in chemical reactions.

In Fig. 3 we shall start with the time-dependent radical concentrations in the anoxic case; for cluster diameter 27 nm and energy 300 eV. OH• radicals and aqueous electrons possess the highest concentrations that decrease rather quickly especially for aqueous electrons. Main radiobiological effect is caused surely by OH• radicals as it is assumed commonly. H• and H_O2• radicals have low concentrations and can hardly contribute to DNA damage.

In Fig. 4 one can see then the concentration dependence at oxygen concentration 0.284 nmol.dm⁻³ (saturated O₂ solution). It is evident that unlike anoxic conditions in the case of saturated O₂ solution the radicals H_O2• may play important role and can contribute significantly to DNA damage.

Conclusion

The presented mathematical model enables us to simulate the chemical stage of the water radiolysis under various oxygen concentrations and to obtain the time dependencies of the concentrations of radicals and other species in corresponding clusters. The Continuous Petri nets make it possible to study the concurrent role of diffusion process and chemical reactions of individual radicals to greater details. The model may be easily extended to involve the influence of other species or radiomodifiers being present (at different concentrations) in water medium during irradiation. In the presented paper we have assumed the spherical symmetry of corresponding radical clusters. The given approach may be easily generalized to assuming also cylindrical symmetry at higher energy transfers. In such a case it will be sufficient to change mathematical expressions characterizing diffusion volume evolution.

The corresponding results may be helpful in studying the damage effect of individual radicals to DNA molecules and, consequently, also for the study of the radiobiological effect on various living cells (see e.g. [1, 2]). They may be useful also in radiotherapy because the oxygen is present in living cells and its concentration in tumour cells may be significantly reduced.

Acknowledgements

This work was supported by the project LG130131 of Ministry of Education, Youth and Sports of the Czech Republic.

Ing. Mgr. Jiří Barilla, CSc.

Department of Informatics

Faculty of Science

E. Purkinje University in Usti nad Labem

České mládeže 8, CZ-400 96 Ústí nad Labem

E-mail: jiri.barilla@ujep.cz