Impact of the torso model on the inverse localization of ischemia

Souhrn

In this simulation study the accuracy of the inverse localization of an ischemic lesion was investigated if a patient-adjusted general torso model and four different approximate heart models were used. Surface ECGs were simulated by a normal heart and by hearts with 18 different ischemic lesions in 7 realistic torso models. Position of each lesion represented by a single dipole was then searched by an inverse solution. Difference QRST integral maps reflecting differences between cardioelectric fields of the ischemic and normal hearts were used. With a standard heart model the mean error of the lesion localization was 3.4 cm. With a standard heart model shifted to an inversely estimated position this error was 3.9 cm, for an equally shifted and properly formed and rotated heart model the error was 2.4 cm and for a heart model properly shifted, formed and rotated the error was 1.1 cm. If realistic CT or MRI-based torso model was used the lesion localization error was 0.7 cm. From the results it can be concluded that use of adjusted standard torso model with properly positioned and formed standard heart model can lead to acceptable accuracy of the inverse localization of an ischemic lesion.

Keywords:
Ischemic lesion, Body surface potential mapping, Inverse solution, Torso and heart model

Introduction

It is believed that local cardiac ischemia caused by occlusion of single coronary artery can be non-invasively assessed by solving the inverse problem of electrocardiology using multichannel surface ECG and proper torso and heart model (its geometry and conductivity). However, accuracy and reliability of the solution can be influenced by many factors such as the number of measured ECG leads, the noise in ECG, selected model of the cardiac generator and inverse method or the fidelity of the used geometrical torso and heart model. In this study we concentrated on the last mentioned factor. It is obvious that an accurate, realistic model of the heart and whole torso based on CT or MR imaging would be desirable. However, in practical situations the whole torso imaging is usually not available and approximate models have to be used instead of it.

In our previous study [1] we have concluded that a general torso shape patient-specifically adjusted according the measured patient chest dimensions with properly positioned electrodes together with an “accurate” heart model yields an acceptable inverse solution. In this simulation study we investigated what accuracy of the inverse solution can be expected if the adjusted general torso shape is used together with various approximate heart models created from a general heart model.

Material and Method

Normal surface ECGs and ECGs corresponding to hearts with single ischemic lesion were first simulated using a well-defined forward model. The simulated ECGs were then used as input for the inverse solution attempting to localize the position of each simulated lesion. Adjusted general torso shape and several heart models were used and their influence on the accuracy of the lesion localization was investigated.

Forward simulation of surface ECGs

Surface ECGs generated by a normal heart and by hearts with 18 different ischemic lesions (Fig. 1) characterized by changed repolarization with action potential shortened by 20% were simulated.

The lesions were modeled as a part of a sphere or ellipsoid in three areas typical for stenosis of one of the three main coronary vessels: anterior (a-) in the region supplied by the left descending artery (LAD), posterior (p-) in the region supplied by the left circumflex artery (LCx) and inferior (i-) in the region supplied by the right coronary artery (RCA). They were located either at the endocardial (-en-) or epicardial (-ep-) surface of the modeled ventricular myocardium. Three lesion sizes were modeled: small (-1) occupying 0.5-1% of the ventricular volume, medium (-2) occupying 2.5-6% and large (-3) occupying 8-14%.

The surface ECGs were simulated in 7 realistic inhomogeneous torso models (6 men, 1 woman) obtained from MRI. While the original torso and lungs shapes were fully preserved, the original hearts were substituted by simplified heart models used for the simulation of the normal and pathological activation but their size, position and rotation were adjusted in agreement with the original heart in that torso (Fig. 2). The potentials bm(t) in 62 surface sites corresponding to an 62-lead ECG system (Amsterdam 62) were computed using the boundary element method: 

bm(t) = A g(t) (1)

where A is the time independent transfer matrix that represents the properties of the inhomogeneous torso model as a volume conductor and g(t) is the multiple dipole generator in particular time instant t of the heart activation. The dipoles represent contributions of activated elements of the ventricular model.

Inverse solution using different heart models

For the inverse localization of each lesion QRST integral maps were used. Their values in 62 surface points are defined as

For identification of the pathological source (the ischemic lesion) the difference QRST integral map between integral maps generated by the normal and pathologically changed heart was used as input:

where g_n(t) and g_p(t) are multiple dipole generators representing the normal and the pathological activation of the ventricular myocardium and Δs represents the integral multiple dipole generator characterizing only the changes of the electrical activity in the modeled lesion.

The equivalent integral generator EIG representing the original integral multiple dipole generator Δs can be then computed from equation (3) as:

EIG = A⁺ Δim (4)

where A⁺ is the pseudoinverse of the transfer matrix A.

This ill-posed problem can be solved in case of local ischemic lesions where the EIG represents only small volume of the myocardium by approximating it by a single dipole. In our method [2] the EIG is computed in predefined possible positions within the ventricular volume that are about 1 cm apart. The position of the lesion is then defined as the location of the EIG that best represents the input data Δim – i.e. the root mean squared difference between the Δim and the map generated by the EIG is minimal.

In the inverse calculations four torso models with standard torso shapes adjusted to particular patient torso, the same standard lungs shapes and containing different heart models were attempted (Fig.3):

• A – general heart model in a standard vertical position defined by the position of the ECG lead V2 and with “standard” rotation,
• B – general heart model vertically shifted to the inversely estimated position by locating the site of the initial ventricular activation to the mid septal region [3],
• C – heart model vertically shifted as in B but properly formed and rotated in agreement with the model used in the forward computation,
• D – heart model properly shifted, formed and rotated in agreement with the model used in the forward computations.

The results for these 4 torso and heart models were compared with the results using the MRI-based torso models used also in the forward calculations.

For each torso-heart model used in the inverse computations two parameters were evaluated:

1. Mean error of the heart model position relatively to the position used in the forward computation,
2. Mean lesion localization error defined as the distance between the gravity center of the simulated lesion and the inversely estimated position of the dipole representing the lesion.

Results

The errors of the heart position for all 5 heart models and all 7 different patient torsos were computed. In all these cases the lesion localization errors for all 18 simulated lesions were also evaluated. The mean values of these errors are shown in Table I.

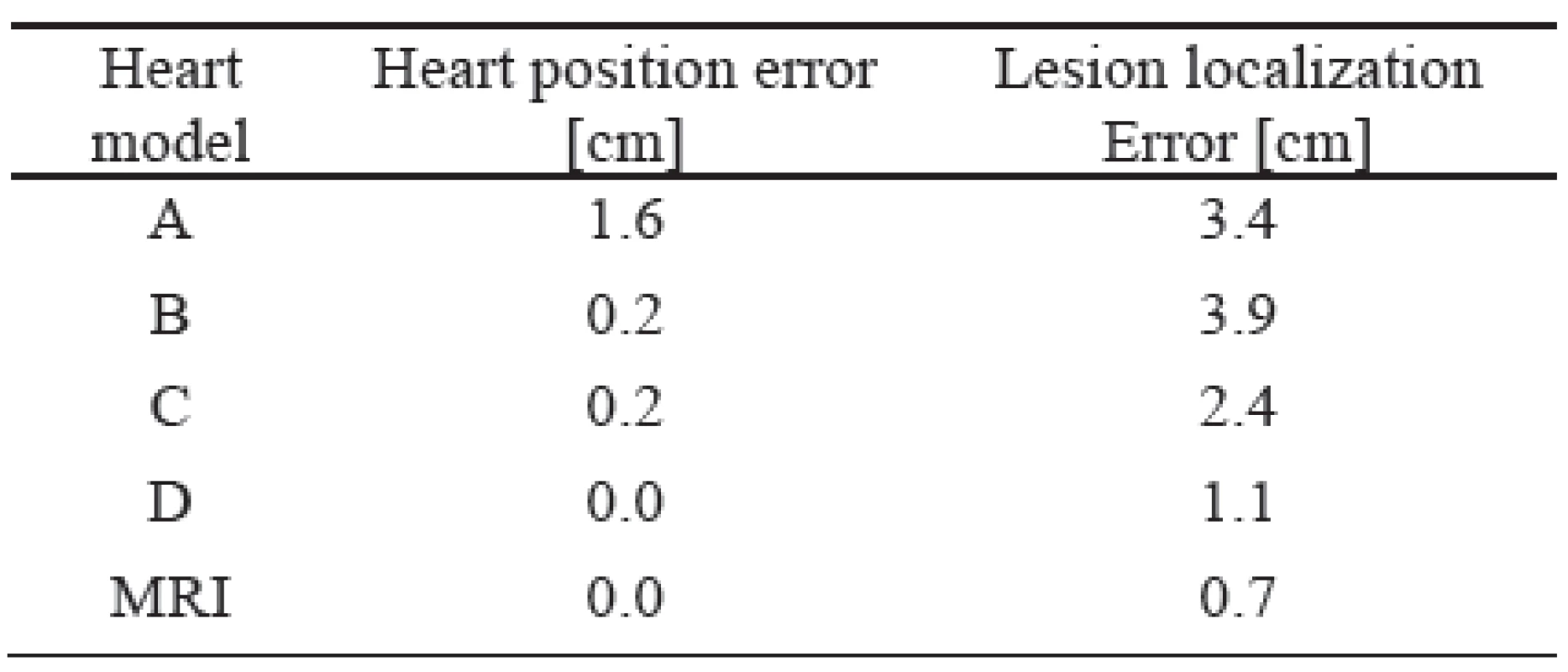
As it can be seen, the worst results were achieved by the unadjusted standard heart models (model A). If the heart model was vertically moved to a position estimated by inverse localization of the initial activation site (model B) the heart position error decreased substantially but the lesion localization error still remained high. Proper forming and rotation of the heart model (model C) did not change the heart position error but decreased the lesion localization error significantly. Additional improvement of the heart model position (model D) decreased the lesion localization error to an acceptable value of 1.1 cm what is comparable with the intrinsic error of 0.7 cm of the used method (model MRI).

For individual cases and lesions the particular values of the lesion localization errors varied in relatively wide range. In Fig. 4 and Fig. 5 examples of “better” and “worse” results are illustrated.

Discussion

As the inverse methods enable the location of the inversely estimated dipoles only to predefined positions, the intrinsic error of the method is dependent on their volume density. In our study the distance between the positions was about 1 cm what led to a reasonable intrinsic “grid error” of 0.7 cm.

Similar as in previous studies, the results showed that the method is not optimal for larger lesions and in such cases a modified method using a cluster of dipoles instead of one dipole performs better [4].

The torso and heart models were selected so that they simulate the conditions that can be expected in real situations. For example, if no imaging is available and only surface dimensions can be measured, the heart model B corresponds to that situation. If the heart size and rotation can be estimated from an ultrasound examination, the heart model C is appropriate. In many cases the CT or MRI of the heart region is available but not of the whole torso. This situation is particularly modeled by the heart model D.

Conclusions

If the whole-torso CT or MRI is not available, a torso model with the shape adjusted to the patient’s chest dimensions and with an approximate, properly positioned, formed and oriented heart model can give acceptable accuracy of the inverse localization of an ischemic lesion represented by single dipole. However, the accuracy of the localization may vary and depends on the available information on the heart size and position.

Acknowledgement

The present study was supported by the research grant 2/0131/13 from the VEGA Grant Agency and by the grant APVV-0513-10 from the Slovak Research and Development Agency.

Jana Lenková

Jana Švehlíková

Milan Tyšler

Department of Biomeasurements

Institute of Measurement Science

Slovak Academy of Sciences

Dúbravská cesta 9, 841 04 Bratislava

Slovak Republic