METHODS FOR AUTOMATIC ESTIMATION OF THE NUMBER OF CLUSTERS FOR K-MEANS ALGORITHM USED ON EEG SIGNAL: FEASIBILITY STUDY

Summary

Lots of brain diseases are recognized by EEG recording. EEG signal has a stochastic character, this stochastic nature makes the evaluation of EEG recording complicated. Therefore we use automatic classification methods for EEG processing. These methods help the expert to find significant or physiologically important segments in the EEG recording. The k-means algorithm is a frequently used method in practice for automatic classification. The main disadvantage of the k-means algorithm is the necessary determination of the number of clusters. So far there are many methods which try to determine optimal number of clusters for k-means algorithm. The aim of this study is to test functionality of the two most frequently used methods on EEG signals, concretely the elbow and the silhouette method. In this feasibility study we compared the results of both methods on simulated data and real EEG signal. We want to prove with the help of an expert the possibility to use these functions on real EEG signal. The results show that the silhouette method applied on EEG recordings is more time-consuming than the elbow method. Neither of the methods is able to correctly recognize the number of clusters in the EEG record by expert evaluation and therefore it is not applicable to the automatic classification of EEG based on k-means algorithm.

Keywords:
silhouette, elbow method, EEG, k-means, automatic determination of number of clusters

Introduction

Electroencephalogram (EEG) is a record of changes of electric potentials from the scalp in time that we measure for detection of some diseases and physiological abnormalities. The experts (electro-encephalo-graphers) visually evaluate the EEG recor-dings, but this evaluation is difficult due to the stochastic nature of the EEG signal. To help the expert, our goal is to automate this process. Therefore we need to split EEG signal into EEG segments (grapho-elements) with similar characteristics. And we sort these segments in the clusters representing different signal characteristic. We use automatic classification algorithms that require input parameters. K-means algorithm is a robust algorithm for automatic classification of signal. Its main input parameter is the number of clusters that is necessary to be defined before classification [1, 2, 3].

The goal of this study is to test methods that can mathematically determine the optimal number of classes for a given data set. We choose two approaches: Silhouettes and Elbow method.

Methods

Data

First type of data sets are simulated data that are created in the programming environment MATLAB R2015a. The simulated data sets consist of objects in 2D feature space that form clusters recognizable by k-means algorithm. Four types of simulated data sets are used (see figure 1). The simulated data sets differ in number of objects and clusters and the distribution in the feature space. Second type of data sets are the three real EEG signal. The EEG recordings were measured in the Bulovka hospital by system BRAINQUICK in standardized conditions for ambulatory EEG. The patients are suspected of epilepsy and these recordings were 15–32 minutes long. All measurements were approved by the ethical commission of the Bulovka hospital. The expert visually determined the correct number of clusters for the epileptic EEG recordings.

Preprocessing

We pre-process the EEG recording in software Wave-Finder (WF). WF is used in clinical practice [4]. We split the EEG recording into segments of similar characteristics by adaptive segmentation (by [5]). Then we calculate features in WF for each segment. We use 24 features in total. These features that are implemented in WF based on practical experience. You can see all features in [6]. We display the results of automatic classification for estimated number of clusters in WF. For the estimation of the number of clusters, we implemented elbow method and silhouettes in programming environment MATLAB R2015a. For automatic classification of the EEG signal, we use k-means algorithm from MATLAB.

The silhouette method

Silhouettes show the consistency of data points inside the clusters, they describe how good the assignment of the point into its cluster is. The silhouette values are calculated based on [8] and they are normalized by maximum, so they range from -1 to 1. The silhouette coefficient close to 1 means that the point is far from neighbouring clusters, the silhouette coefficient close to 0 means that the point is between two neighbouring clusters and silhouette coefficient close to -1 means that the point may be assigned to a wrong cluster. If most of the points have negative silhouette values, then we need to classify the data again to different number of clusters. The advantage of the silhouette analysis is its broad application. This silhouette analysis can be combined with any classification method based on the distance measure (e.g. k-means) and the silhouette analysis is not restricted to one metric, but any metric can be used for calculation of the distance [7, 8, 9].

The elbow method

The elbow method is the oldest method for estimating the number of clusters [10]. The elbow method is widely used in many studies [11]. This method must run through all possible results of number of clusters, like the silhouette method. The estimated number of clusters is the point, where the difference of consequence information values rapidly decreases. In our case the obtained information value is a variance of objects in clusters. The elbow method plots graph, where there is variance on y axes and number of clusters on x axes. We find point of graph, where is the biggest band, called elbow. In our study we use sum of inter-clusters variance on y axes [10, 11, 12].

Results

Simulated data

We used all four types of simulated data for validation of estimated of the ideal number of clusters by methods silhouette and elbow. We tested correct estimation of the number of clusters and real computation time for both methods. Simulated data 1 included 2 clusters. Both methods correctly estimated number of clusters (see figure 2 and 3). Simulated data 2 included 3 clusters. Both methods correctly estimated number of clusters (see figure 4 and 5). Simulated data 3 included 3 clusters. Both methods correctly estimated number of clusters (see figure 6 and 7). Simulated data 4 included 5 clusters. Both methods correctly estimated number of clusters (see figure 8 and 9). The real computation time of both methods is compared for simulated data in table 1. The table shows that the silhouettes have higher real computation time than the elbow method.

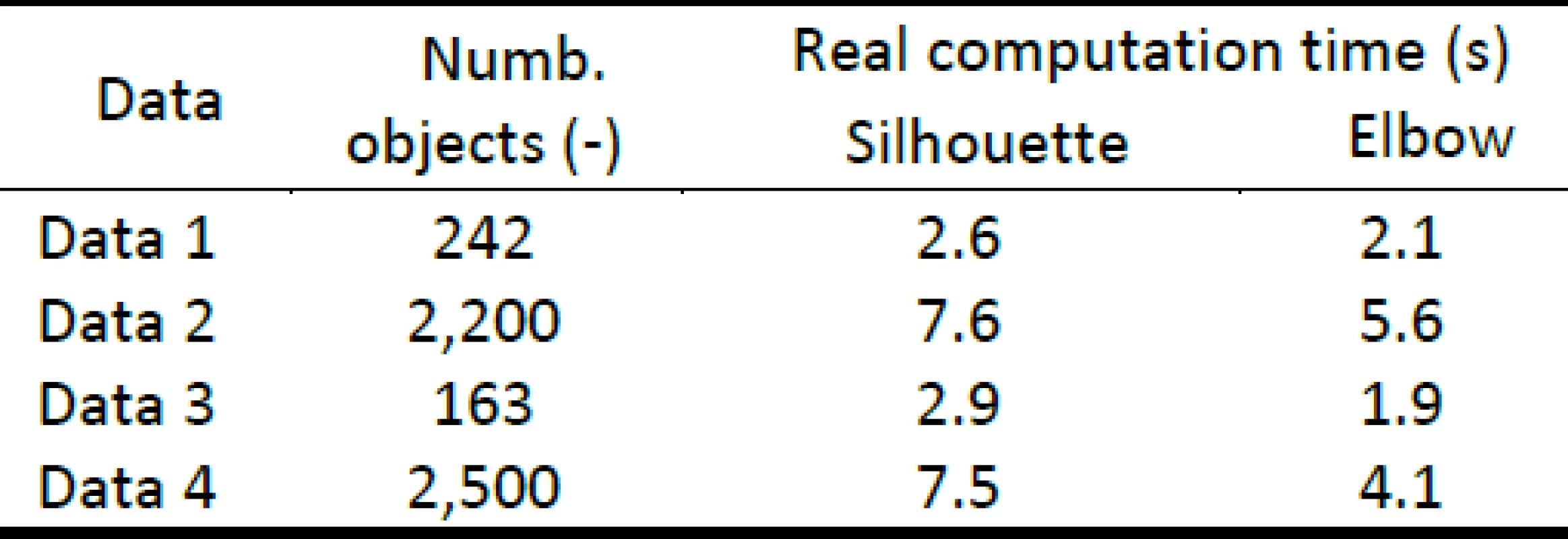
Real EEG signal

We tested both methods on 3 real EEG signals. The silhouettes had higher real computation time than the elbow method for real EEG signal. For example, real computation time of the silhouettes was 82.95 minutes for signal EEG 1 (see table 2). The real computation time was rising with higher number of segments included in EEG signal for both methods.

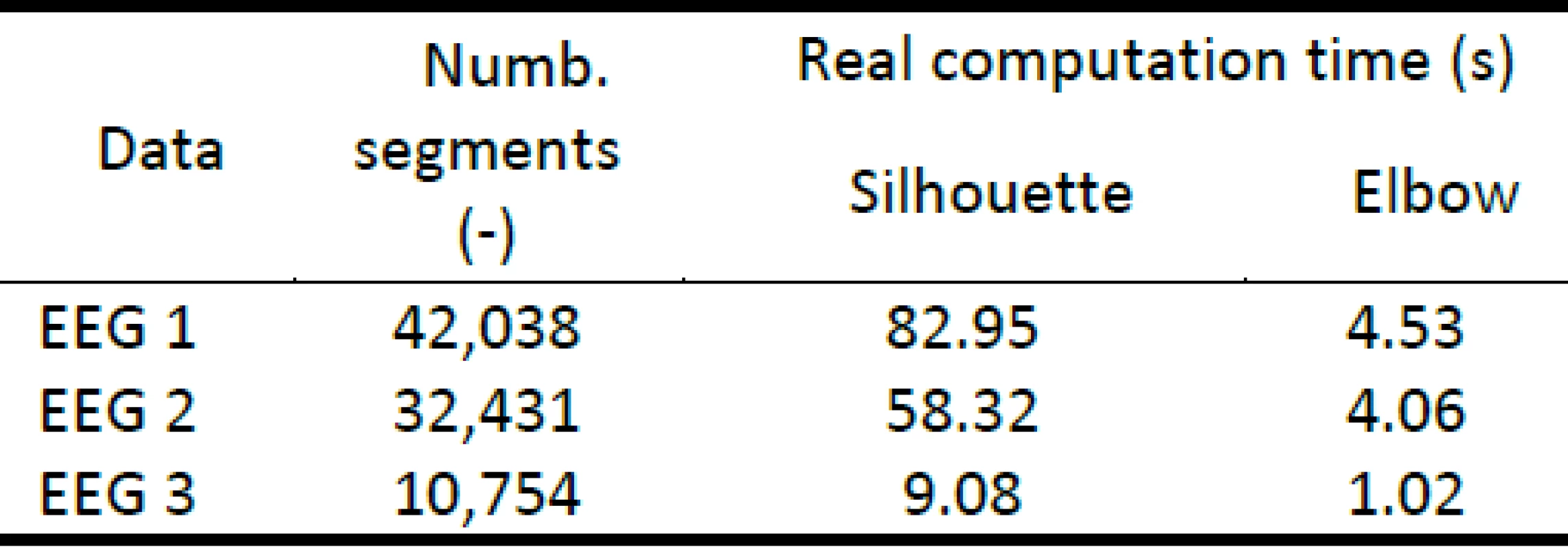
The elbow method detected two possible results of the number of clusters. One of detected number of clusters was 2 in every tested EEG signal for this method. The silhouettes detected 2 as number of clusters in every tested EEG signal (see figures 10–13). The expert determined that 2 clusters cannot be used in clinical practise (see figures 14–15). We can get higher information about classification using k-means algorithm by dimensional reduction. We reduced feature space by PCA method and we observed classification of the 2D EEG feature space using the k-means algorithm with different number of clusters (see figures 15–16).

Discussion

We used 4 types of simulated data with known number of clusters for validation. The results imply that both methods found correct number of clusters for all tested simulated data in 2D features space. The silhouettes are more time-consuming than the elbow method. However, real computation time of the silhouettes for maximum number of simulated testing objects (2500 obj.) was only 7.5 seconds (see table 1). We used 3 real EEG recordings for testing the applicability of both methods on EEG signal. The estimated number of clusters is determined by the expert for each EEG recording. The number of segments of one EEG recording ranges between 10,754 and 42,038 segments in 24-dimensional feature space. On such a high number of segments the silhouettes are computed for a longer time than the elbow method for this real EEG data sets (see table 2). The largest number of segments computed by the silhouettes in one EEG recording took 82.95 minutes. This disadvantage decreases the usability of the method on real EEG recording analysis in clinical practices. One of the main disadvantage of the elbow method is that it recognized more than one point in graph for our real EEG data that can represent the best estimation of the number of clusters (see figure 13). This ambiguity may be caused by non-separability of clusters in feature space in use k-means algorithm. We can see examples of results of 2D reduced feature space after use k-means classification in figures 16 and 17. These figures may indicate a problem of k-means algorithm with classification of EEG feature space. The silhouettes estimated 2 clusters in every EEG recording tested. The expert identified this estimation as unusable in practise. In figures 14 and 15 we can see that 2 clusters divide the EEG recording only in "distinct" and "less distinct" segments which does not reflect the medical meaning of segments. The elbow method detected 2 as one of the potential estimations of the number of clusters, but it detected also another possible number of clusters for every tested EEG recording. We can choose one of these points only after an expert entry to distinguish the more suitable number of clusters, so the elbow method is redundant in the case that the expert still needs to entry the process.

Conclusion

In this study, we compared two methods for determining the appropriate number of clusters for automatic classification of EEG by k-means algorithm. The compared methods are the silhouette and the elbow method. We verified the functionality of both methods on simulated data, then we tested these methods on 3 real EEG records. The silhouette method is more time-consuming than the elbow method, but the elbow method suggests more than one possible number of clusters which is not consistent with our goal of automatic classification. However, one of the suggested numbers of clusters was always 2 as well as the number of clusters suggested with the silhouette method. The expert visually evaluated the result after k-means classification into 2 clusters and observed that 2 clusters are not sufficient for classification of EEG in practise. This mistake can be based on itself k-means classification. Both tested methods for automatic classification of the number of clusters are looking for the ideal number of clusters. Compared to that, k-means algorithm can’t find the ideal cluster layout in 2D reduced PCA feature space. In the future work we want tested, whether this rule also applies to multidimensional feature space and whether the extraction of other features can improve efficiency of tested methods for automatic estimation of the number of clusters for EEG signals.

Acknowledgement

The work has been supported by the Grant Agency of the Czech Technical University in Prague, grant number SGS15/229/OHK4/3T/17 with topic: Modular hierarchical support system for EEG analysis and by the Grant Agency of Czech Republic with topic: Temporal context in analysis of long-term non-stationary multidimensional signal, register number 17-20480S and by project LO1611 under the NPU I program.

Ing. Jan Štrobl

Department of Biomedical Technology

Faculty of Biomedical Engineering

Czech Technical University in Prague

nám. Sítná 3105, CZ-272 01 Kladno

E-mail: strobja1@fbmi.cvut.cz

Phone: +420 224 357 996