-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Analýza dat v neurologii. VII.
Reprodukovatelnost a opakovatelnost měření u spojitých dat
Autoři: L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů: Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2008; 71/104(1): 106-109
Kategorie: Okénko statistika
V minulém díle seriálu jsme se věnovali hodnocení reprodukovatelnosti a opakovatelnosti u diskrétních dat. Ovšem i u spojitých dat je toto hodnocení vyžadováno jako doklad kvality a serióznosti experimentální práce. A obdobně jako u dat diskrétních se zde v zahraniční literatuře operuje s pojmy inter-observer a intra-observer variabilita. Význam těchto pojmů se přechodem na spojitá data nijak nemění, zásadně se ale mění možnosti hodnocení.
U diskrétních dat nabývajících pouze omezeného počtu hodnot je analýza reprodukovatelnosti i opakovatelnosti založena na sledování frekvence shody v měření (viz též díl VI seriálu). Ve srovnání s tím nabízejí spojitá data širší možnosti, včetně instruktivních grafických znázornění. Logicky jsou tyto testy povinnou komponentou hodnocení kvality u diagnostických zkoušek a obecně u laboratorních měření.
Reprodukovatelnost je stejně jako u diskrétních dat nadřazeným pojmem, neboť sleduje výsledky opakovaných měření prováděných různými experimentátory. Předpokládáme tedy, že reprodukovatelné výsledky umožňují zavádění postupů v různých laboratořích, protože reprodukovatelnost výstupů mohou kontrolovat nezávislé osoby a instituce. Opakovatelnost vyjadřuje shodu opakovaného měření určité sady vzorků „v sérii“ od stejného experimentátora. K měření reprodukovatelnosti i opakovatelnosti je možné použít totožné vzorky. Nejjednodušší možný příklad, kdy je měření provedeno pouze 2x uvádí tab. 1.
Tab. 1. Číselný příklad pro hodnocení opakovatelnosti a reprodukovatelnosti měření spojitého znaku. 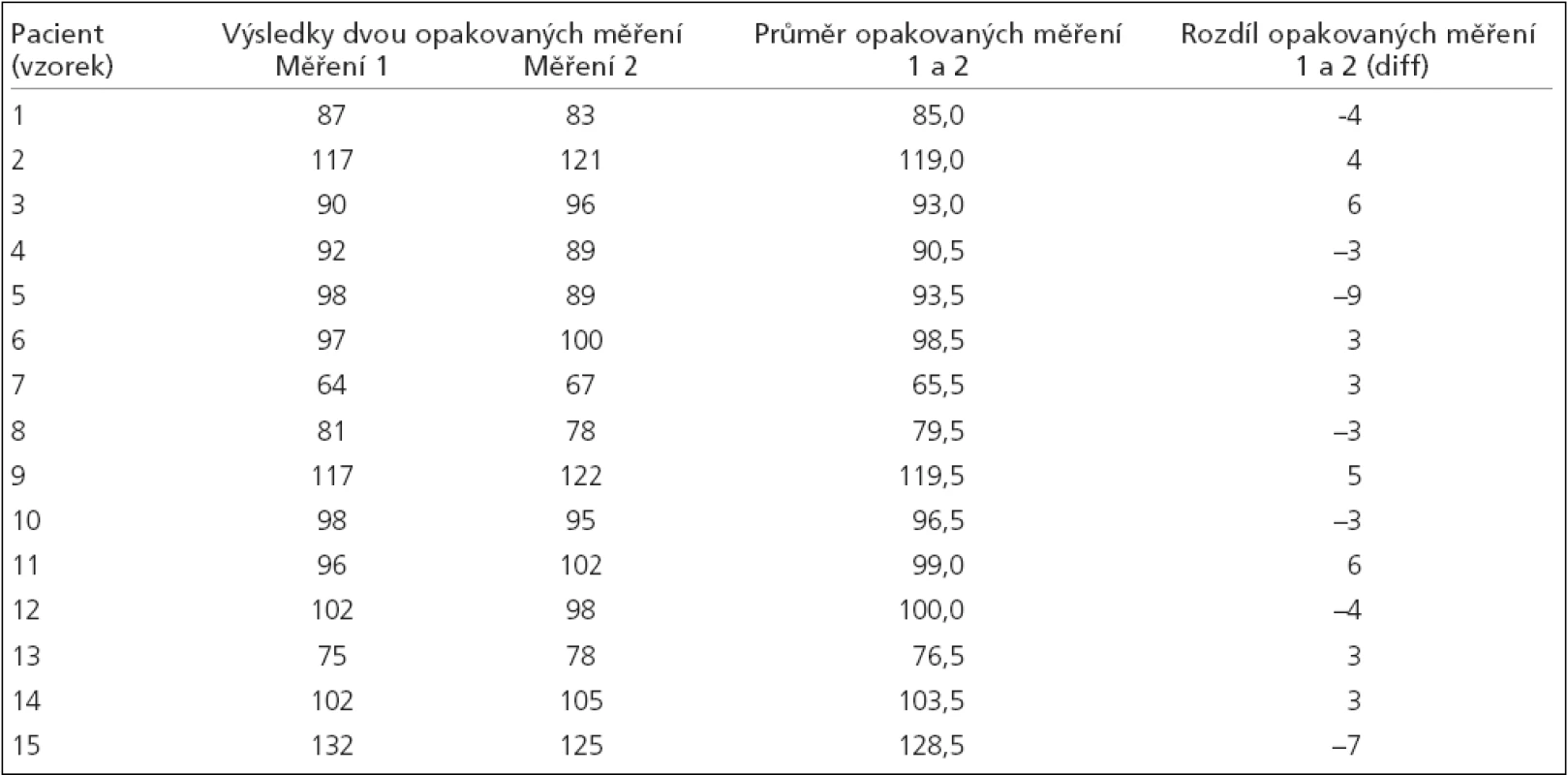
Měření 1 a 2 zde představují opakování experimentu nebo měření sady 15 vzorků. Podle toho, zda měření provedla jedna osoba nebo dva různí experimentátoři budeme hovořit o opakovatelnosti nebo reprodukovatelnosti výsledků. Obojí by nastalo ze 100 %, pokud by všech 15 párů měření poskytlo přesně stejný výsledek, což u hodnocení běžných biologických nebo chemických znaků v praxi nemůže nastat. Musíme tedy prověřit, o kolik se opakovaná měření liší (označeno jako sloupec diff) a vyhodnotit míru shody anebo neshody.
Hodnocení reprodukovatelnosti a opakovatelnosti je tedy kvantitativní analýzou odchylky opakovaných měření téhož znaku. Nejprve počítáme diference opakovaných měření (diff) a následně odhadujeme jejich průměr (̄xdiff) a směrodatnou odchylku (sdiff). Hodnota sdiff bývá označována jako směrodatná odchylka opakovatelnosti nebo reprodukovatelnosti. Další postup lze shrnout v následujících bodech:
- Vyhodnotíme, zda se průměr diferencí neliší od nuly. V ideálním případě je x̄diff přesně rovno nule (viz příklad v tab. 1) nebo se od nuly odchyluje jen nepodstatně. Významná odchylka průměru diferencí od nuly indikuje systematickou chybu („bias“), kdy jedno z opakovaných měření vede systematicky k vyšším nebo nižším hodnotám něž měření druhé. Odchylku průměru diferencí od nuly lze prověřit statistickým testem (např. t-test) nebo pro ni lze spočítat interval spolehlivosti.
- Vypočítáme tzv. limity shody opakovaných měření (limits of agreement). Za předpokladu, že diference opakovaných měření mají normální rozložení, můžeme limity pro výskyt 95 % diferencí počítat jako x̄diff ± 1,96*sdiff (místo 1,96 se používá i zaokrouhlená hodnota 2). Příklad v tabulce 1 vede k dolní hranici intervalu -9,6 a symetricky k horní hranici +9,6. Pokud jsou tyto limity v praxi akceptovatelné jako hranice přijatelného rozdílu opakovaných měření, pak je lze využít jako míru reprodukovatelnosti nebo opakovatelnosti. Pokud diference opakovaných měření dané hranice překračují, nelze měření označit za reprodukovatelná (opakovatelná).
- Použijeme grafické znázornění dle práce Bland a Altman (1986). Tento dnes již standardní graf (nazývaný téměř familiárně Bland&Altman plot) je znázorněn na obrázku 1a. Jednoduše vynášíme průměr opakovaných měření na osu X a jejich diference na osu Y. K ose Y jsou dále zakresleny pozice průměrné diference (v našich datech přesně 0) a pozice 95% limitů shody (viz výše výpočet v bodě 2).
Závěr hodnocení modelového příkladu z tabulky 1 je, že opakovaná měření 1 a 2 se podstatně neliší a splňují podmínku výskytu 95 % diferencí v intervalu ± dvě směrodatné odchylky (Bland a Altman, 1986). Průměrná diference je nulová a nepředpokládáme tedy žádné systematické zkreslení u opakovaně měřených hodnot.
Výše uvedené nastavení 95% limitů shody je funkční pouze při splnění předpokladu normality rozložení diferencí opakovaných měření. Tento předpoklad je nutné prověřit testy i graficky (např. histogram), k jeho posouzení významně přispěje i graf dle práce Bland a Altman (1986). Graf znázorněný na obrázku 1a umožní nejen posoudit shodu opakovaných měření, ale snadno identifikuje odlehlé body i jiné odchylky od normality (viz níže diskuze k obrázkům 3-4).
Limity shody x̄diff ± 1,96*sdiff se vztahují k výskytu všech diferencí v populaci a nelze je považovat za interval spolehlivosti odhadu x̄diff . Ten můžeme odhadnout dle standardního vzorce, s využitím standardní chyby odhadu průměru počítané jako sdiff /√n. Místo standardizovaného normálního rozložení zde musíme použít kvantil Studentova rozložení t pro n-1 = 14 stupňů volnosti. U dat z tabulky 1 je standardní chyba průměru diferencí 1,3 a kvantil t0,975 = 2,1. Můžeme tedy kalkulovat 95% interval spolehlivosti pro x̄diff s hranicemi ± 2,7. Obecně je interval spolehlivosti výpočet užitečný jako hodnocení systematického zkreslení opakovaných měření (bias). Jelikož je ale v našich datech průměr diferencí roven přesně nule, výpočet nemohl žádnou odchylku od nuly prokázat. Obdobně lze vypočítat i intervaly spolehlivosti pro spodní a horní limit shody. Zájemce o tento výpočet odkážeme na práce Bland a Altman (1986, 1999).
Pro praktickou práci s limity shody je nutné uvést ještě následující poznámky:
- Mezinárodně se používá alternativní termín „CR = coefficient of repeatability“. Jde jen o jiný název pro již uvedené 95% limity shody: CR = 1,96*[Σdiff2/(n-1)]1/2 = 1,96*sdiff. CR je tedy hranice, kterou za podmínek opakovatelnosti nebo reprodukovatelnosti nesmí absolutní hodnota diference opakovaných měření překročit.
- Limity shody se samozřejmě v praxi nepoužívají dogmaticky a z hodnocení je možné vyloučit ojedinělé zřetelně odlehlé body. Odlehlé body snadno identifikujeme na grafu, který modelově ukazuje obr. 1a.
- V praxi může nastat situace, kdy doporučené 95% limity shody nevyhovují, a to i přesto, že jde o dlouhodobě uznávaný standard (např. BSI, 1975). Je-li změna řádně zdůvodněna, lze využít jiné pravděpodobnostní hranice (90%, 99% apod.) anebo statistické hodnocení doplnit empirickým intervalem, který vychází ze znalosti dané metody měření, norem apod.
- Metodiku hodnocení reprodukovatelnosti lze také využít pro hodnocení shody různých metod, pokud měří stejnou veličinu. Příkladem může být posouzení nově zaváděné metody ve srovnání se starým postupem.
Obr. 1. Grafické hodnocení opakovatelnosti a reprodukovatelnosti měření spojitého znaku (data z tab. 1). 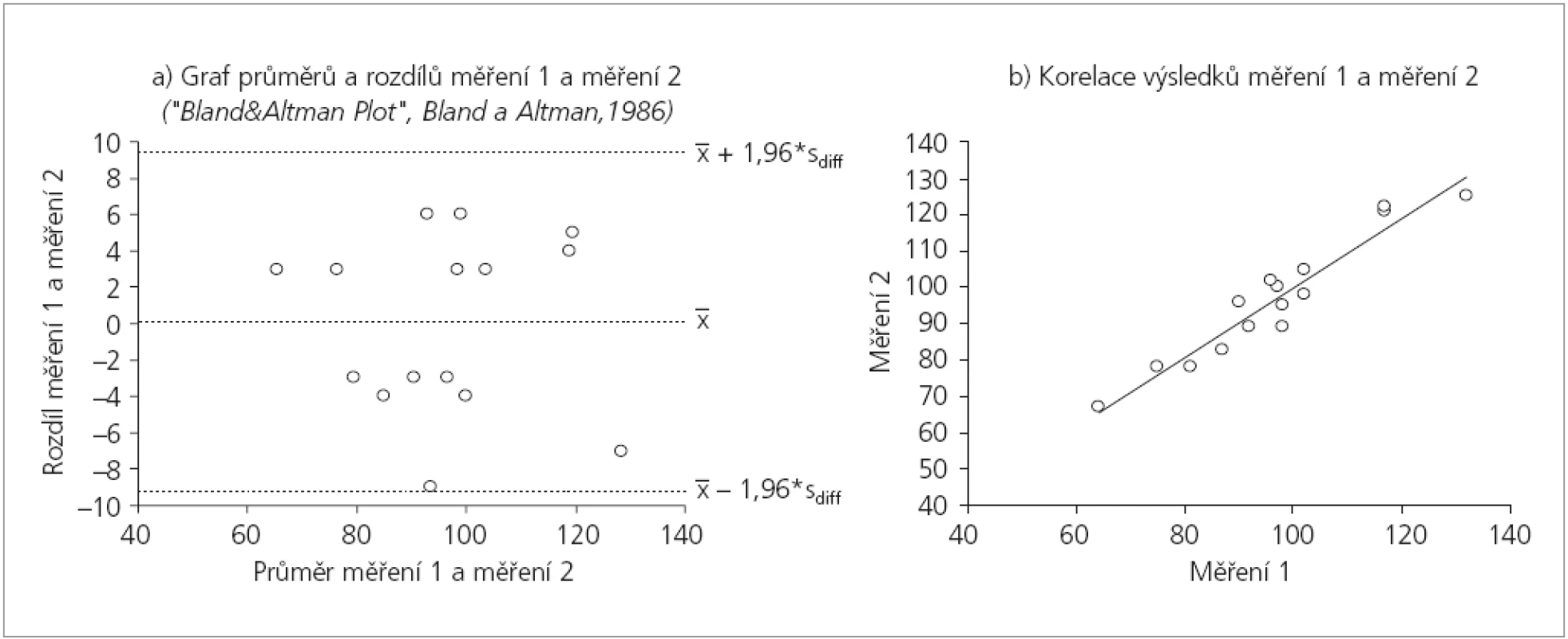
Hodnocení opakovatelnosti a reprodukovatelnosti musí pracovat s kvantitativními rozdíly opakovaných měření. Nelze je nahradit jinými mírami jako například korelací mezi opakovanými měřeními. Sám fakt, že opakovaná měření mezi sebou významně korelují ještě neříká nic o jejich skutečné shodě. Opakovaná měření mohou na dvourozměrném grafu vytvářet téměř ideální přímku, tato ale může mít různý sklon a může maskovat systematické nadhodnocování nebo podhodnocování některého z experimentátorů. Proto je korelace jako míra opakovatelnosti nebo reprodukovatelnosti zcela nepřijatelná. Nízký informační potenciál korelačního grafu je patrný i na obrázku 1b. Obr. 2a-b dále zobrazují situace, kdy hodnocení indikuje rozdílný rozsah diferencí mezi opakovanými měřeními. Korelační koeficient mezi měřeními by tyto rozdíly vůbec neodhalil.
Obr. 2. Ukázka interpretační hodnoty grafů dle práce Bland & Altman (1986) ve dvou modelových situacích. 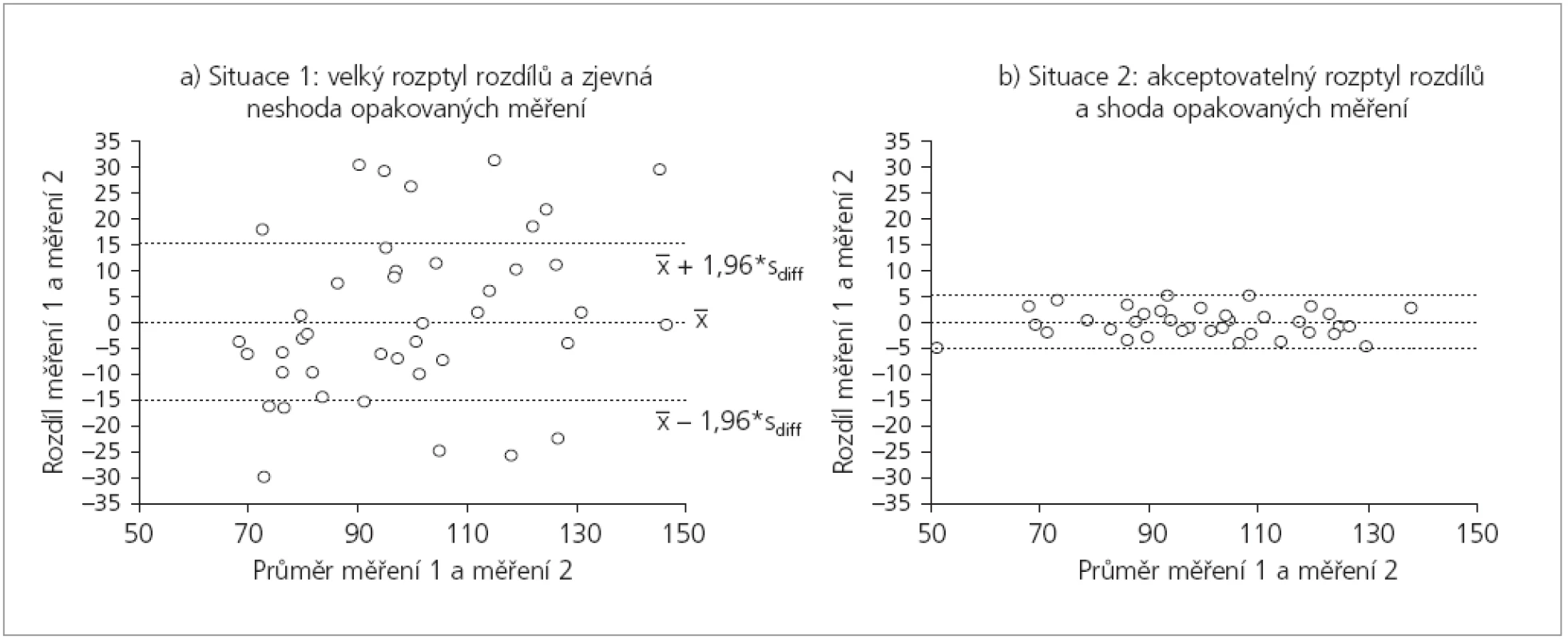
Z grafů dle práce Bland a Altman (1986) lze vyčíst i další skutečnosti, které dokumentují příklady na obr. 3–4:
- Zjistíme-li, že diference opakovaných měření (osa Y) souvisí s hodnotou měřené veličiny (osa X), musíme tuto skutečnost prošetřit. Na obrázku 3 je znázorněna situace, kdy diference narůstají s rostoucí hodnotou znaku. Zde téměř vždy pomůže logaritmická transformace (obr. 3a a 3b). Obecně jakýkoli vztah mezi hodnotami diferencí a hodnotami měřeného znaku indikuje narušení předpokladu normality rozložení a musí být prověřen.
- Diference opakovaných měření mohou vykazovat systematický rostoucí nebo klesající trend s rostoucí hodnotou měřeného znaku (obr. 4a) anebo se mohou v průměru významně odchylovat od nuly (obr. 4b). Obě situace ukazují na vážné systematické zkreslení opakovaných měření a je nutné prošetřit jejich příčinu v primárních datech.
Obr. 3. Rostoucí hodnota diferencí opakovaných měření s velikosti měřeného znaku (a) a řešení pomocí logaritmické transformace (b). 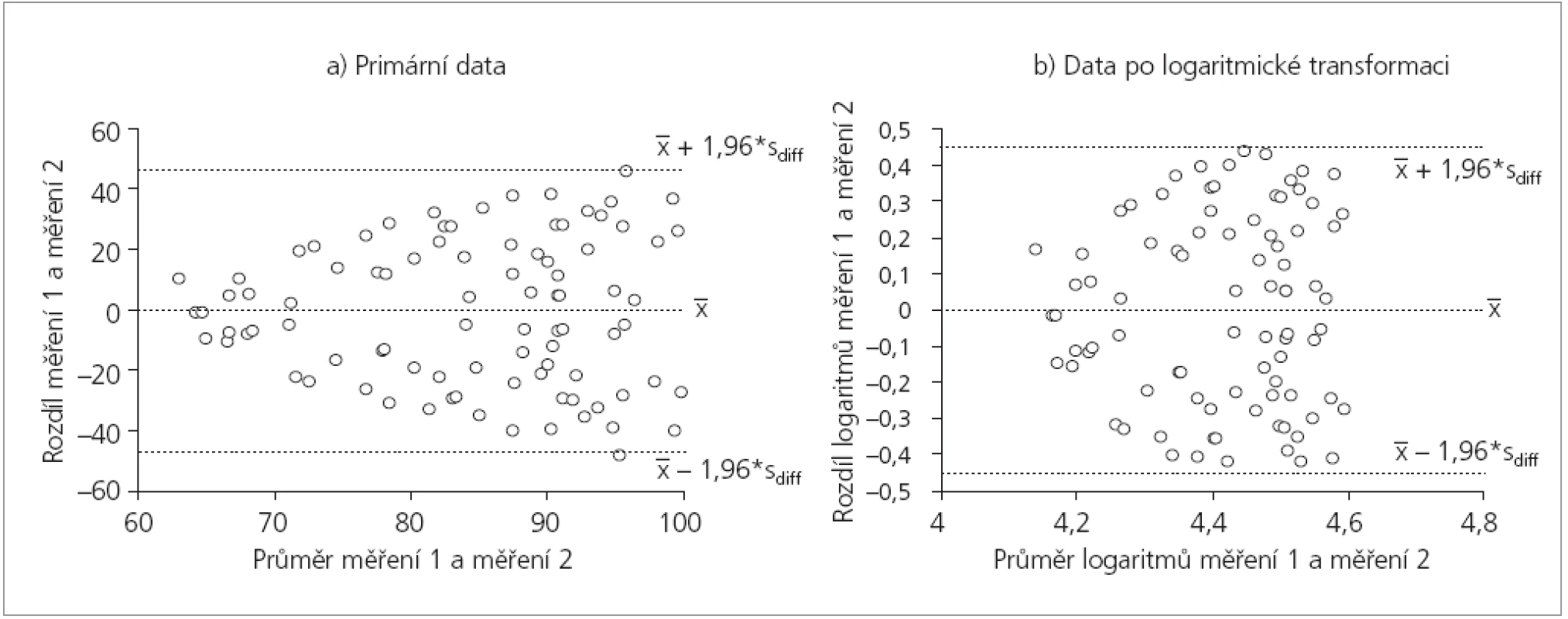
Obr. 4. Ukázky situací s pravděpodobným systematickým zkrelením opakovaně měřených hodnot. 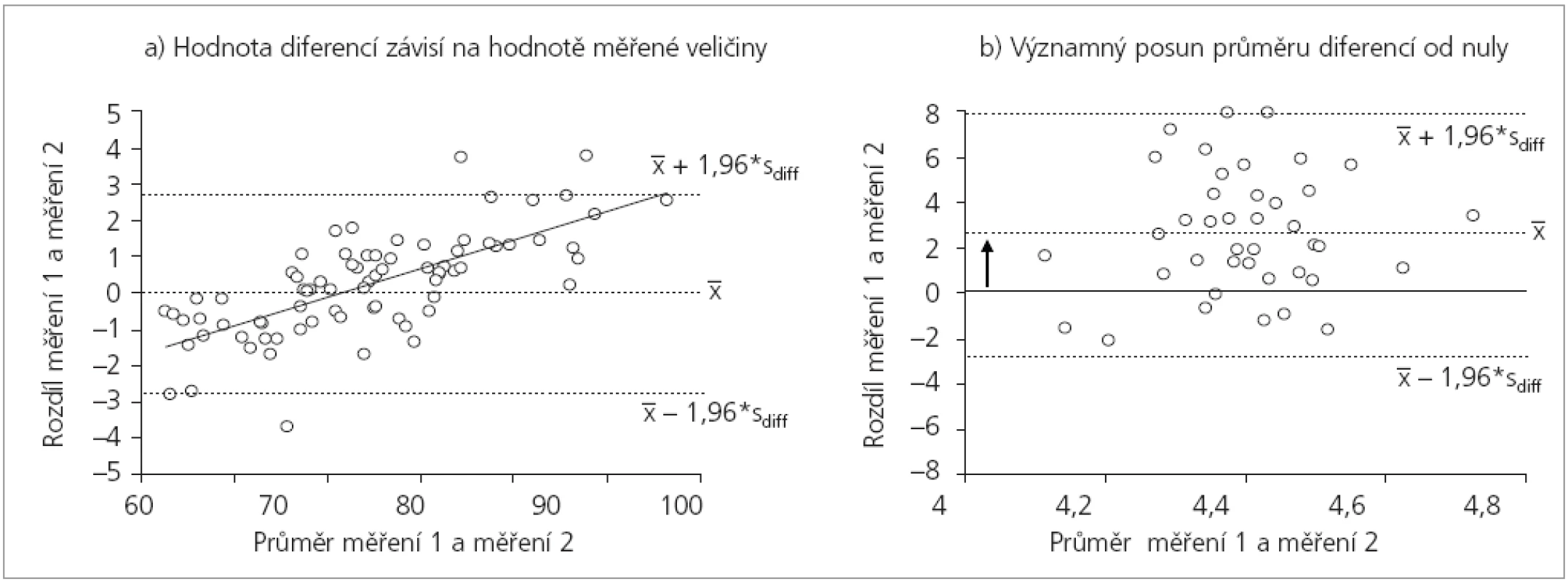
Jak vidno, k testování opakovatelnosti a reprodukovatelnosti máme k dispozici jednoduché početní i grafické nástroje. Zvídavé čtenáře jistě napadne, že všechny zde uvedené příklady pracovaly pouze se dvěma opakovanými měřeními. Jak ale postupovat v případě, kdy je opakovaných měření více? Pokud máme data opakovaných měření pro každého ze zapojených experimentátorů, je nutné korigovat odhad rozptylu diferencí. Hodnocení není ani v těchto případech nijak složité, ale výklad překračuje plánovaný rozsah tohoto dílu. U více než dvou opakovaných měření dále přichází ke slovu analýza rozptylu, kterou se budeme zabývat v některém z příštích dílů seriálu. Nicméně i u takových dat můžeme plně uplatnit zde prezentované výpočty a grafy navržené Blandem a Altmanem. O významu jejich práce z roku 1986 svědčí i fakt, že dosáhla téměř 10 000 citačních ohlasů. Jednoduchý a velmi chytrý nápad tak evidentně pomohl tisícům vědeckých prací. Věříme, že si uvedené grafy oblíbíte i vy a testy opakovatelnosti přestanou být vaším problémem.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz,
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
1. Barek J et al. Metrologická terminologie v chemii. Chem Listy 94, 439 – 444 (2000).
2. Bland JM, Altman DG (1986) Statistical method for assessing agreement between two methods of clinical measurement. The Lancet, i, 307-310.
3. Bland JM, Altman DG (1999) Measuring agreement in method comparison studies. Statistical Methods in Medical Research, 8, 135-160.
4. Dewitte K, Fierens C, Stöckl D, LM Thienpont (2002) Application of the Bland-Altman plot for interpretation of method-comparison studies: a critical investigation of its practice. Clinical Chemistry, 48, 799-801.
5. BSI (1975). British Standards Institution. Precision of test methods 1: Guide for the determination and reproducibility for a standard test method (BS 597, Part 1). London: BSI (1975).
Štítky
Dětská neurologie Neurochirurgie Neurologie
Článek Webové okénkoČlánek Dopis redakciČlánek Dopis redakciČlánek ÚvodníkČlánek Myasténia gravis
Článek vyšel v časopiseČeská a slovenská neurologie a neurochirurgie
Nejčtenější tento týden
2008 Číslo 1- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Magnosolv a jeho využití v neurologii
- Moje zkušenosti s Magnosolvem podávaným pacientům jako profylaxe migrény a u pacientů s diagnostikovanou spazmofilní tetanií i při normomagnezémii - MUDr. Dana Pecharová, neurolog
- Nejčastější nežádoucí účinky venlafaxinu během terapie odeznívají
-
Všechny články tohoto čísla
- Myastenie s pozitivními anti-MuSK protilátkami u mladého muže: kazuistika
- Webové okénko
-
Analýza dat v neurologii. VII.
Reprodukovatelnost a opakovatelnost měření u spojitých dat - Dopis redakci
- Dopis redakci
- Cohen-Gadol AA, Spenser DD. The Legacy of Harvey Cushing. Stuttgart, New York: Thieme 1999. ISBN973-3-13-147861-0.
- Anderson DG, Vaccaro A. Decision Making in Spinal Care. Stuttgart, New York: Thieme 2000. ISBN 3 13 140481-7.
- Klinické využití protilátek u roztroušené sklerózy
- Idiopatické generalizované epilepsie s typickými absencemi v dospělosti
- Difuzní gliomy mozkového kmene u dětí. Noční můra dětského onkologa.
- Bezpečnosť MRI vyšetrenia u pacientov s kovovými implantátmi a implantovanými prístrojmi
- Komentár k článku Nevrlý et al. Ovlivnění plazmatické hladiny homocysteinu u pacientů s Parkinsonovou chorobou terapií L-DOPA a entacaponem.
- Ovlivnění plazmatické hladiny homocysteinu u pacientů s Parkinsonovou chorobou terapií L-DOPA a entacaponem
- Úvodník
- Efekt nízké dávky manitolu na sérovou osmolalitu
- Komentář ke článku Charvát F et al. Mechanická embolektomie pomocí MERCI katétru u nemocných s akutním uzávěrem mozkových tepen.
- Mechanická embolektomie pomocí Merci katétru u nemocných s akutním uzávěrem mozkových tepen
- Myasténia gravis
- Komplementarita stentingu a endarterektomie karotid: tříleté zkušenosti
- Ageneze laterálního semicirkulárního kanálku: kazuistika
- Případ multifokální encefalitidy reagující na léčbu steroidy jako příčiny obtížně zvládnutelných epileptických záchvatů frontálního laloku
- Vznik neuritidy optického nervu v důsledku mukokély vedlejších nosních dutin - příčinná souvislost či koincidence? Kazuistika
- Mikroskopický nález kryptokoka v mozkomíšním moku jako první příznak rozvinutého stadia AIDS. Kazuistika
- Komentář ke článku Ehler E, Latta J. Myastenie s pozitivními anti-MuSK protilátkami u mladého muže: kazuistika
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Bezpečnosť MRI vyšetrenia u pacientov s kovovými implantátmi a implantovanými prístrojmi
- Difuzní gliomy mozkového kmene u dětí. Noční můra dětského onkologa.
- Myasténia gravis
- Klinické využití protilátek u roztroušené sklerózy
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



