The effect of the size of a conical hopper aperture on the parameters of the flow equation of sorbitol and its size fractions

Overview

Determination of the rate of gravitational flow through a hopper aperture is one of the most widely used methods for the evaluation of flowability properties of pharmaceutical materials. This work studies the influence of the diameter of a conical hopper aperture in the range of 0.6–1.5 cm on the mass flow rate Q (g/s) of the pharmaceutical excipient, sorbitol, for direct compression (Merisorb 200, MS 200) and its size fractions in the range of 0.080–0.400 mm in order to recommend the appropriate aperture size for testing. Non-linear dependence of the flow rate on the aperture diameter is modeled by the Jones-Pilpel power equation. Using the actual parameters of the power equation, the precision of the mass flow rate prediction was the basic criterion in optimization of the orifice diameter. It was detected experimentally that for the evaluation of the flow rate of MS 200 and its size fractions in the range used a 1.0 cm aperture is recommended, which allows the most precise prediction of the flow rate.

Key words:
particulate material • excipient, flow equation • conical hopper • size fraction

Introduction 

An important characteristic of pharmaceutical powders is flowability, which expresses the ability of powder substances to flow. The flow behavior is dependent not only on the material’s characteristics such as particle size and shape, adhesiveness, moisture content, etc.^1–4), but also on the conditions in which the flow behavior is specified, e.g. external conditions and equipment used.

It is possible to observe different kinds of flow behavior of particulate matter during the flow. During the unloading of the hopper a variety of different flow problems can take place. Detailed information provided, e.g., by the authors Prescott & Barnum⁵⁾. The conditions for each material, in which the flow experiences no significant problems, should be experimentally determined.

The correct description of the flowability properties is important not only for handling, storage and transportation of powder materials, but in pharmaceutics it is very important for the processes of blending, homogenization and dosing of active substances and excipients in the manufacturing of dosage forms, such as tablets or gelatin capsules. If, during filling, the mixture of powder substances has inappropriate flowability properties, then tablets or divided powder in gelatin capsules fail to comply with the requirements of content or mass uniformity. In pharmaceutical technology, the inappropriateness of flow of powder materials is solved, e.g., by adding lubricating substances or increasing the size of particles by granulation process.

Flow behavior of powders depends on their physicochemical and mechanical properties, and its characterization is very difficult, because the individual test methods are not able to sufficiently and, above all, completely, describe the properties of powders. The results of the flowability evaluations carried out in different laboratories are therefore often significantly varied, which is mainly due to large quantities of wide-spread methodologies of measurement, different types of measuring instruments, and especially the lack of a standardized measuring procedure. In pharmaceutical technology, the flowability evaluation is performed using pharmacopoeial methods of powder assessment (Ph. Eur., 2.9.36.), such as angle of repose⁶⁾, expression of the compressibility index and the Hausner ratio and the rate of flow through the aperture. Other assessment methods are used in technical testing and evaluating flow such as shear and avalanching behavior of powder materials^{4–5, 7–9)}.

The mass flow rate Q (g/s) through the hopper aperture is considered one of the best methods of flowability evaluation. This method is suitable for free-flowing materials. The condition is to achieve a uniform flow of material with minimal amount of failures. The literature also recommends optimum geometry of the test hopper to achieve this state. Normalized geometry takes into account the relationship between the diameter of the hopper D, the hopper aperture diameter D₀, the particle diameter x and the height of the hopper H.

It is recommended that: D > 2.5D₀, D – D₀ > 30x, D₀ > 6x, H > D, H > D₀ with a choice of different aperture diameter¹⁰⁾. The optimal (uniform) flow rate is not set and the success of an accurate estimate of the flow rate for a variety of hoppers is limited¹¹⁾. Increasing the accuracy of the estimation of the flow rate is therefore a constant focus for a number of research teams.

As already mentioned, the flow rate is primarily influenced by the diameter of the hopper aperture, the particle diameter and bulk density. The relationship between these variables is described by the flow equation. One of the most frequently used ones is the Brown and Richards power equation [1] which describes the flow rate of monodisperse particulate materials through the hopper aperture¹²⁾,

where Q is the mass flow rate (g/s), d is the true powder density (g/ml), g is the acceleration of gravity (cm/s²), x is the particle diameter (cm) and D₀ is the diameter of the hopper circular aperture (cm), k (dimensionless) is the empirical shape coefficient and π/4 is quadrature of the circle (dimensionless). The expression (k . x) is interpreted as the “empty annulus“ and describes the corrected influence of the hopper wall. Dependence of the flow rate on the diameter of the hopper is transformed by a constant exponent 5/2. It was discovered that the shape coefficient is usually in the range of 1 ≤ k ≤ 2¹³⁾.

The Beverloo et al equation [2]¹⁴⁾, which is also frequently used, is derived from equation [1].

 

The parameters of the equations are empirical discharge coefficient C ~ π/4 (dimensionless), and the previously mentioned shape coefficient whose value k = 1.4 is used as a constant. Instead of the true powder density, the equation introduces bulk density d_b, which describes the behavior of powders during flow and is more easily measurable. It is usually stated that the validity of equations [1] and [2] is limited to particles greater than 0.500 mm, respectively 0.200 mm¹⁵⁾.

In pharmaceutical technology, the Jones & Pilpel empirical equation [3] can also be used¹⁶⁾,

where A and n (the reciprocal value of the exponent) are dimensionless parameters of the equation, d_b is the powder bulk density (g/ml) and g, D₀ and Q were as already mentioned above.

This work evaluates the effect of the diameter of the conical hopper aperture on the mass flow rate Q (g/s) of sorbitol for direct compression (MS 200) and its fractions in the range of 0.080–0.400 mm with the goal of recommending the appropriate diameter for the hopper aperture D₀ (cm) to achieve the highest precision of the reverse prediction of the flow rate.

Experimental part

Materials

Sorbitol for direct compression (Merisorb 200, Tereos Syral SAS Nesle), of pharmaceutical quality was used. Sample MS 200 was characterized by a mean particle diameter x₅₀ = 0.123 mm and x₉₀ = 0.214 mm by the analytical sieving methods (Vibratory Sieve Shaker AS 200 basic, RETSCH, Germany) in accordance to European Pharmacopoeia (Ph. Eur., 2.9.38); the moisture content in the material of 0.79% ± 0.03% was determined (N = 3) gravimetrically (XM60, PRECISA, Switzerland).

The MS 200 size fractions were obtained by sieving (Vibratory Sieve Shaker AS 200 basic, RETSCH, Germany) with the use of the following sieves: 0.080 mm, 0.125 mm, 0.200 mm, 0.300 mm, and 0.400 mm. In Table 1, the particle diameter x (mm) is referred to as geometric mean of the used range of the sieves.

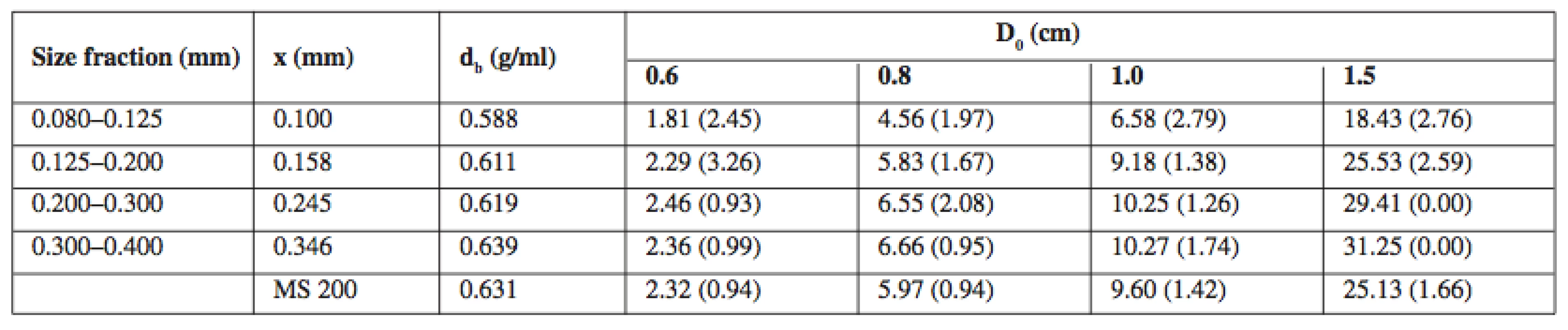
Methods

All measurements were carried out at a temperature in the range of 21 °C ± 1°C and relative air humidity in the range of 29% ± 2%.

Bulk density

The bulk density of MS 200 and its size fractions was determined by Scott’s volumeter (COPLEY, SOTAX, UK) in accordance with the European Pharmacopoeia (Ph. Eur., 2.9.34). The powder was layered into a cylindrical stainless cup with volume of 25.00 ml ± 0.05 ml. The distance between the powder heap and the cylindrical stainless cup was 1.9 cm. The excess powder was carefully removed so as to avoid any compression, tapping or losses of powder from the cup. The bulk density d_b (g/ml) was calculated from a known volume of the cylindrical cup, and the weight of the powder. Table 1 lists the means for ten repetitions of measurements, the relative standard deviations (RSD) were less than 1%.

The flow rate Q (g/s) through the test hopper aperture

To measure the flow rate of MS 200 and its size fractions the Automated Powder and Granulate Testing System was used (PTG S3, PHARMATEST, Germany). The mass flow rate Q (g/s) was determined by measuring the time it took to empty a 50.0 g of powder through a stainless steel conical test hopper with a capacity of 300.0 ml. For the measurements, the following sizes of the aperture diameter were used: 0.6 cm, 0.8 cm, 1.0 cm, and 1.5 cm. The selected aperture was fixed on the bottom part of the hopper. After unblocking the aperture, the pass-through time was measured automatically with an accuracy rating of 0.1 s. The uniform mass flow rate was detected by graphical registration. The flow rate of MS 200 and its fractions was then calculated from the discovered pass-through time. Table 1 lists the means for ten repetitions of measurements, the relative standard deviations (RSD) in % are provided in brackets.

Mathematical model

The results have been modeled using the equation [3]. The accuracy of the reverse prediction of the flow rate Q_p  (g/s) was expressed as the percentage deviation Δ (%) between the experimentally noted flow rate and that calculated by the generated flow equation.

Results and discussion

Particulate materials are the most common materials used in the manufacturing of dosage forms. The exact description of their flow behavior is essential to ensure the continuity of the production process and the quality of the final products. An appropriate method of evaluation is measuring the flow rate Q through the test hopper aperture. Achieving uniform flow without faults is a main requirement. In order to achieve this, the appropriate diameter of the hopper aperture D₀ should be determined experimentally.

Table 1 summarizes the overview of properties of sorbitol for direct compression (MS 200). The size fractions are characterized by the particle diameter x (mm), the bulk density d_b (g/ml) and the mass flow rate Q (g/s) depending on the diameter of the circular aperture of the conical test hopper D₀ (cm). Geometrical requirements for the test hopper and the progress of measurement have been in compliance with the recommendation^10–11). The uniformity of flow was monitored by using a graphical record of the quantity of poured material in time. No malfunctions were observed during the flow for the tested size fractions, not even for the smallest fraction with a mean diameter of 0.100 mm.

With increasing the size of the aperture, the flow rate increases non-linearly. This dependency can be mathematically described by a power equation, which is usually referred to as the flow equation. The experimentally determined flow rates Q (g/s) of Merisorb 200 and its size fractions (Table 1) were modeled using the Jones-Pilpel power equation [3]¹⁶⁾.

Calculation of the parameters of the equation A and n is possible due to the graphical dependencies between (Q/√g.π/4.d_b) and the size of the aperture D₀ (cm). The parameters of the flow equation [3] A and n are given in Table 2. The results are supplemented by the correlation coefficient r in the range of 0.9950–0.9966 which demonstrates that the mathematical model describes experimental data with a high degree of accuracy. Parameter A (dimensionless) expresses the correction of the influence of the hopper wall and its values are in the range of approximately 1.15–1.34. The values of the exponent n are in the range of approximately 2.5–2.8, with a mean value of 2.6.

When testing the flow, it is usually necessary to first select an appropriate diameter of the aperture. The criterion for the proposal of the optimal diameter of the hopper aperture can be the precision of the individual reverse estimates of the flow rate Q_p (g/s) of MS 200 and its size fractions through the individual test hopper aperture D₀ (cm). In the used range of D₀ = 0.6–1.5 cm, the flow equation parameters A and n (Table 2) were used in the estimation of Q_p (g/s) according to the equation [4],

Comparing the reverse estimate of the flow rate with the experimentally obtained value of Q, percentage deviations Δ (%) between the two values could be subsequently expressed. The results are listed in Table 3. The accuracy of the reverse estimate of the flow rate for all of the hopper apertures (i.e. without discern to the aperture diameter) for polydisperse MS 200 is approximately 7% and is comparable with the precision for monodisperse fractions in the range of 0.080 mm – 0.400 mm, which ranges from 5.5% to 7.7%. The mean deviation in the last column of Table 3 allows for an expression of the optimal diameter of the hopper aperture D₀ (cm) for the flow of MS 200 and its size fractions in the studied range of 0.080–0.400 mm. Regardless of the fraction size and the minus or plus sign, the lowest mean deviation has been recorded for the aperture of 1.0 cm as is evident from Table 3.

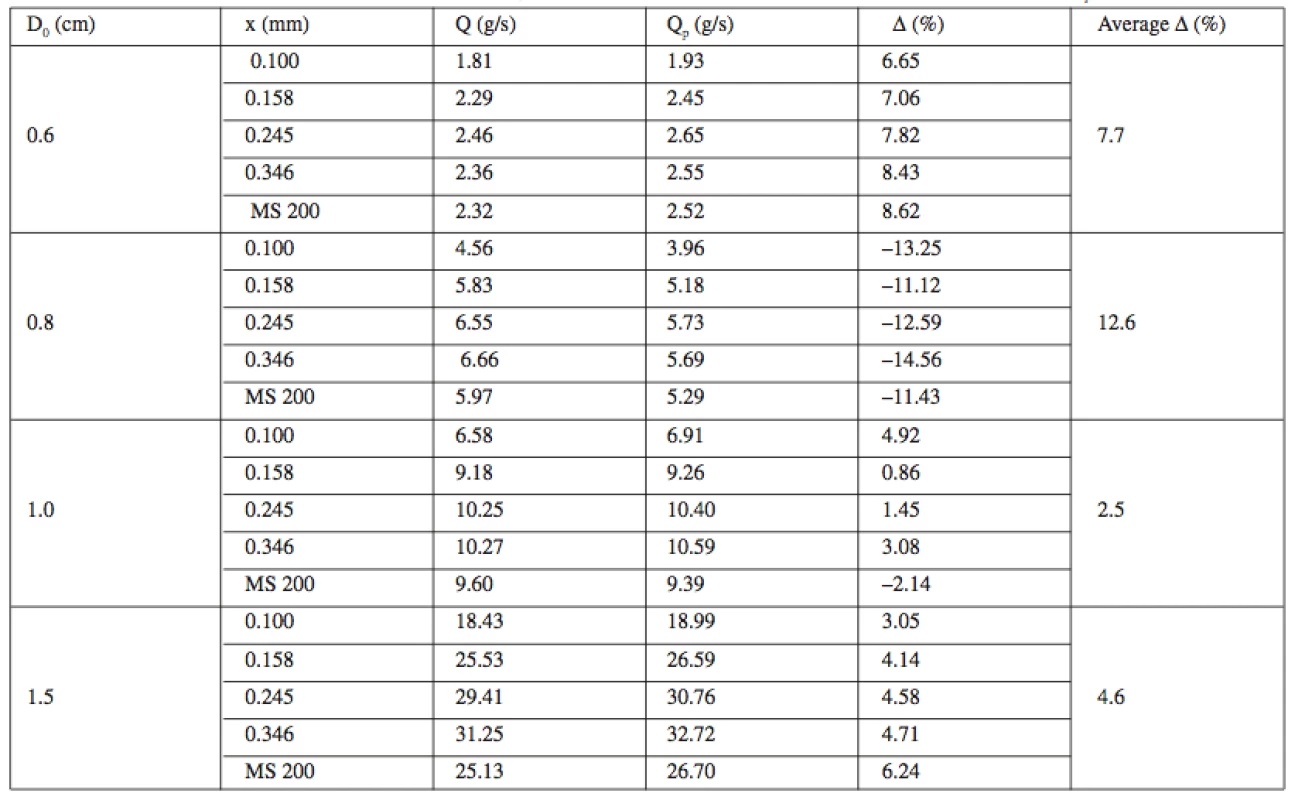
Conclusions 

The mass flow rate of sorbitol and its size fractions through the conical hopper aperture is non-linearly influenced by the size of the test hopper aperture D₀. On the basis of the experimental results, it is possible, for evaluation of flow rate of sorbitol MS 200 and its fractions in the studied range of 0.080–0.400 mm and in the used range of aperture diameters of 0.6–1.5 cm, to recommend aperture of 1.0 cm, for which a mathematical model used allows the most precise estimate of the flow rate (g/s), characterized by the lowest average deviation from the experimentally observed flow rate of 2.5%.

Acknowledgement

The authors wish to express their thanks to the grant No. 322315/2015 of Grant Agency of Charles University in Prague and the specific research project SVV 260 183 of Charles University in Prague for the financial support, and to Dr. Müller Pharma Ltd. for lending the Automated Powder and Granulate Testing System, PTG S3 (PHARMATEST, Germany). 

Conflicts of interest: none.

Received 23 February 2015

Accepted 16 March 2015

doc. PharmDr. Zdenka Šklubalová, Ph.D. • H. Hurychová

Charles University in Prague, Faculty of Pharmacy

Department of Pharmaceutical Technology

Heyrovského 1203, 500 05 Hradec Králové, Czech Republic

e-mail: zdenka.sklubalova@faf.cuni.cz