-
Medical journals
- Career
Srovnatelnost výsledků vyšetření – možné postupy
Authors: J. Ambrožová
Authors‘ workplace: OKB-H Nemocnice Prachatice, a. s.
Published in: Klin. Biochem. Metab., 30, 2022, No. 2, p. 37-47
Overview
Klíčový problém srovnávacích experimentů kvantitativních postupů měření představuje stanovení mezí shody, které jsou platné pro celý rozsah měřených hodnot v dané studii. Pouze tak je možné správně data interpretovat a dosáhnout adekvátních závěrů. V rámci dostupných regresních metod jde o to navrhnout tu nejvhodnější k určení vztahu mezi navzájem porovnávanými postupy měření a popsat silné a slabé stránky těchto technik pro dané datové soubory.
První část práce uvádí klíčové body aktualizovaného CLSI pokynu EP09c, Porovnávání postupů měření a odhad vychýlení (bias) pomocí vzorků pacientů [2], jehož 3. vydání vyšlo v roce 2018. Část druhá předkládá praktický příklad srovnávacího experimentu s pomocí dostupných statistických SW nástrojů zvláště vhodných k použití ve srovnávacích experimentech.
Klíčová slova:
bias – Srovnávací experiment pro kvantitativní postupy měření – vizualizační techniky – regresní techniky – vyhodnocení
Úvod
Pokyn Clinical Laboratory Standard Institute EP09c je určen k přímé aplikaci na postupy měření, které poskytují kvantitativní numerické výsledky, a jeho záměrem je dosáhnout globální harmonizace zajišťující srovnatelnost kvantitativních výsledků vyšetření klinických laboratoří i výrobců. Nabízí postupy, jak provádět účinnou, správnou analýzu dat prostřednictvím standardních experimentálních a statistických metod. Doporučuje ověřené postupy stanovení vychýlení resp. bias mezi dvěma kvantitativními postupy měření a identifikuje faktory, které je třeba vzít v úvahu při navrhování plánu srovnávacího experimentu sloužícího k porovnávání a analýze dvou kvantitativních postupů měření s použitím vzorků pacientů. Poskytuje návody, jak tvořit rozdílové a bodové grafy pro vizuální kontrolu a popis dat, a uvádí různé metody účinné kvantifikace vztahu mezi dvěma postupy měření, tj. předkládá možnosti způsobů odhadu bias např. prostřednictvím regresních technik.
Norma ISO 15189 v platném znění, článek 5.6.4 Srovnatelnost výsledků vyšetření stanoví: „Musí být definovány způsoby porovnávání používaných postupů, zařízení a metod a stanovení porovnatelnosti výsledků vzorků pacientů v klinicky relevantních intervalech. Takové porovnávání zahrnuje stejné či různé postupy, zařízení, různá místa nebo na vše uvedené“. Cílem tohoto sdělení je podat stručný návod, jak tento požadavek normy s pomocí doporučených statistických postupů splnit. Tematicky lze při srovnávání kvantitativních postupů měření čerpat z řady dostupných literárních zdrojů, za všechny zde uvádím dva [1,2].
Pokyn CLSI [2] oproti předchozím vydáním klade hlavní důraz na:
• Vizualizaci dat pomocí rozdílových grafů
• Popisy regrese v rámci volitelných analytických technik (jednoduché lineární, Demingovy a Passing - Bablokovy regrese)
• Měření bias pomocí rozdílových grafů
• Měření bias v bodech klinického rozhodování
• Výpočet intervalů spolehlivosti pro všechny parametry
• Detekci odlehlých hodnot
Pokyn CLSI [2] pracuje výhradně s platnou terminologií dle TNI 01 0115 Mezinárodního metrologického slovníku. Míra pravdivosti měření, která není veličinou, tj. nemůže být vyjádřena číselně (viz míry pro těsnost shody pravdivosti - ISO 5725) je zde vyjadřována jako bias a dosud používaný měřicí interval, je nahrazen termínem vydávaný rozsah, který je označen r[a;b], a odkazuje se na „soubor hodnot měřené veličiny, pro který má chyba měřicího přístroje (testu) ležet ve stanovených mezích“. Interval [a;b] je vymezen dvěma limity a a b, kde (b > a), zatímco rozsah (r[a;b]) je vyjádřen jako rozdíl mezi b minus a (b - a).
Vzhledem ke složité povaze výpočtů je důrazně doporučováno, aby uživatel pokynu měl zajištěn přístup k počítači resp. k softwaru (SW) vhodnému pro statické zpracování dat.
Srovnávací experiment kvantitativních postupů měření
Srovnávací experiment kvantitativních postupů měření (zde SEKPM) je založen na výsledcích získaných pomocí dvou různých kvantitativních postupů měření z experimentálního výběru pacientských vzorků a představuje jednu z nejběžnějších technik, kterou velmi využívají jak výrobci, tak klinické laboratoře ke srovnávání dvou postupů, které měří stejnou veličinu. Cílem SEKPM je odhadnout vychýlení (bias) tzv. kandidátského měřicího postupu in vitro diagnostiky (IVD) vzhledem k ověřenému komparátoru tj. srovnávacímu postupu měření. V tomto smyslu zadání jsou definovány dvě různé úrovně srovnávání postupů měření dle jejich účelu v rámci SEKPM:
• zaváděcí a validační, které provádějí výrobci a jsou určeny ke zjišťování vhodnosti k danému účelu,
• verifikační, které provádějí klinické laboratoře a jsou určeny ke zjišťování shody s deklaracemi výrobce.
Obligátně se předpokládá, že tzv. referenční postup měření vždy poskytuje „skutečné“ hodnoty, a proto se v rámci takového experimentu srovnávání provádí přímo i odhad vychýlení tj. bias čili odhad systematické chyby měření (SE).
Za srovnávací postup měření (ověřený komparátor) lze považovat:
• uznávaný referenční postup měření,
• postup měření používaný výrobcem v definovaných požadavcích,
• stávající postup měření ověřený v dané klinické laboratoři někdy považovaný za tzv. „zlatý standard“.
V běžné praxi mnohdy standardní ani referenční postup měření k dispozici není. Proto i výrobci IVD obvykle srovnávají kandidátský postup měření s postupem nejvhodnějším, aktuálně dostupným. Klinické laboratoře tak činí zcela běžně, když např. nový produkt IVD zaváděný do testovací nabídky (kandidátský postup) srovnávají s postupem měření v laboratoři dosud používaným.
Za situace, kdy klinická laboratoř potřebuje kvantifikovat a následně analyzovat rozdíl mezi postupem měření, který má být zaveden, a tím, který právě používá, bývá stávající postup měření nejpravděpodobnější volbou komparátoru. V každém případě je nutné přijmout fakt, že jakýkoliv srovnávací postup měření, jiný než referenční, může mít určitou zranitelnost vůči interferujícím látkám a účinkům matrice. Ve srovnávacím experimentu navíc „skutečná“ hodnota nemusí být známa, pak se spíše než „bias“ zjišťuje „rozdíl“ obou postupů. Výsledkem SEKPM by měla být objektivní kvantifikace vztahu mezi oběma srovnávanými postupy, a výsledek může být vyjádřen buď jako vychýlení (bias) na zvoleném rozsahu měření nebo bias určité hodnoty měřené veličiny. Cílem SEKPM může být také ověření výrobcem deklarovaného vychýlení (popř. rozdílu) či jeho nezávislá kvantifikace. Zjištěné vychýlení pak může pomoci určit, jestli a jaké změny je třeba provést při vydávání výsledků poskytnutých kandidátským postupem měření.
Odběr a manipulace se vzorky – požadavky
Určení vztahu mezi kandidátským a srovnávacím postupem měření se doporučuje realizovat pomocí neupravených vzorků pacientů, u nichž výsledky měřené veličiny pokrývají běžně vydávaný rozsah měření. Vzorky pacientů je obligátně nutno odebírat a následně s nimi manipulovat pouze v souladu s uznávanou správnou laboratorní praxí a doporučeními výrobců. Je-li žádoucí provádět opakovaná stanovení nebo uchovávat dostatek vzorku pro případná opětovná testování a zároveň potřebný objem vzorku nelze získat od jednoho pacienta, je povoleno tvořit jakési „minipooly“ smícháním vzorků od více pacientů (nejlépe dvou), vždy však s přibližně stejnou koncentrací měřené veličiny a podobnou historií onemocnění.
Provádějí-li se srovnávané postupy měření v různých lokalitách, může být zapotřebí vzorky určené pro SEKPM řádně uskladnit v místech, kde byly odebrány. V takovém případě by laboratoř měla zajistit, aby změny související s poškozením nebo zhoršením v důsledku přepravy nebo skladování žádný srovnávaný postup měření neovlivnily. Pokud vzorky byly pro oba postupy rozděleny a postupy měření to umožňují, mělo by se s nimi vždy v obou postupech měření zacházet obdobným způsobem.
K měření každého vzorku srovnávacím a kandidátským postupem by vždy mělo dojít v časovém rozpětí konzistentním se stabilitou měřené veličiny. Pokud je to možné, je doporučeno odebrat i použít vzorky k analýze v týž den. Vzorky by měly být skladovány a uchovávány identickým způsobem, který spolehlivě zajistí jejich stabilitu, splňuje podmínky skladování stanovené výrobci obou postupů měření a tím pádem vylučuje nutnost zavedení podmínky skladování jako proměnné.
Stejně rozdělené vzorky, pokud je to možné, by měly být změřeny oběma srovnávanými postupy měření zhruba ve stejnou dobu, a to dle předem stanoveného plánu SEKPM. Synchronizace je méně kritická, jsou-li vzorky skladovány zmrazené. Může to být nezbytné, nacházejí-li se dva srovnávané analytické systémy, na nichž se postupy měření realizují, v různých lokalitách. Jsou-li vzorky rozděleny do skupin určených k měření v předem daných časech, v ideálním případě by stejně označené skupiny vzorků měly být zpracovány v týchž časech oběma postupy měření (např. skupina jedna se provádí v den jedna na obou analytických systémech). Jsou-li zjištěny u konkrétního výsledku vzorku jakékoliv problémy, každé další opakování testu by se mělo provést co nejdříve.
Pokyn [2] doporučuje klinickým laboratořím k řádnému zjištění vychýlení (bias) nebo rozdílu mezi postupy měření změřit alespoň 40 vzorků pacientů, které spadají do běžně vydávaného rozsahu měření obou postupů měření. V každém postupu měření se typicky provádí měření jednoho neopakovaného vzorku. S cílem snížit výslednou nejistotu odhadu vychýlení však lze, pokud to objem vzorku a časové limity z obou postupů měření dovolí, použít i průměrný výsledek vícenásobných opakování měření vzorků.
Měření každého jednotlivého objektu se v praxi zdravotnické laboratoře obvykle provádí jen jednou, v singletu. Cílem SEKPM vždy zůstává získat nejlepší odhad přesnosti metody nebo průměru změřené hodnoty u daného objektu, k čemuž lze samozřejmě s výhodou použít opakovaných měření. Pokud to vedení klinické laboratoře považuje za vhodné, jsou pro každý srovnávaný postup měření běžně přijatelná jednotlivá měření. Naopak, je-li k dispozici více opakování měření téhož vzorku, měly by se naměřené koncentrace každého vzorku zprůměrovat a za odhad výsledku pak považovat vypočítaný průměr nebo medián opakovaných měření. Základním předpokladem zprůměrování výsledků je, že opakování každého měřícího postupu na daném vzorku je pokusem měřit vždy stejnou, neměnnou veličinu a že průměrování snižuje nejistotu odhadu měřené veličiny ve vzorku. Počet opakování měření může, ale nemusí být omezen.
Následující proces shromažďování dat musí zajistit přesný, úplný a včasný sběr výsledků SEKPM, včetně zaznamenání jakýchkoli chyb v experimentu nebo přístrojů.
Vizuální kontrola získaných dat
Každý proces kvantifikace bias začíná důkladnou vizuální kontrolou souborů dat pořízených oběma srovnávanými postupy měření v rámci srovnávacího experimentu, přičemž prvotní situační přezkum dat na přítomnost výjimečných nebo odlehlých hodnot mohou dobře zprostředkovat i grafy krabicové. Nicméně k zásadní vizualizaci souborů dat doporučuje pokyn [2] bodové a rozdílové grafy, které odhalí základní charakteristiky variability vztahu navzájem srovnávaných metod, a jsou proto velmi důležitým nástrojem následné volby vhodné analytické techniky. Údaje z rozdílových grafů lze také použít k přímému odhadu vychýlení mezi oběma postupy měření. V praxi ovšem stále ještě existuje mnoho zrádných neznalostí o validitě, výhodách či nevýhodách různých rozdílových grafů [3].
Bodový graf zobrazuje výsledky SEKPM tak, že výsledky měřené veličiny srovnávacího postupu měření (xi) se vynášejí na osu x a výsledky získané v kandidátském postupu (yi) měření na osu y.
Rozdílový graf zobrazuje výsledky SEKPM, tak že výsledky měřené veličiny stanovené srovnávacím postupem (xi) se uvádějí na horizontální ose x a rozdíly (di) mezi výsledky kandidátským a srovnávacím postupem měření (xi -yi) na vertikální ose y. Nejčastěji používaným příkladem rozdílového grafu je Bland-Altmanův graf.
Podstatná část [2] se věnuje právě rozdílovým grafům určeným a priori k vizualizaci vztahu mezi oběma srovnávanými postupy měření s cílem pomocí nich určit základní charakteristiky variability zkoumaného vztahu, a především zjistit, zda se v rámci vydávaného rozsahu měření vyskytuje buď konstantní (konstantní SD) nebo procentuální (konstantní CV) rozdíl. Při verifikaci metod v klinické laboratoři lze také rozdílové grafy využít přímo k odhadu bias stanovením průměru nebo mediánu rozdílů. Zjištění vyplývající z inspekce grafů rozdílů následně také pomáhají při odhadu bias prostřednictvím přímky regresního proložení, při odhadech jejího sklonu (směrnice) a průsečíku, ale také k přímému odhadu bias na zvolených koncentracích.
Čtenář [2] si na základě dvou volitelných faktorů musí vybrat ze čtyř typů rozdílových grafů. První faktor volby grafů je dán tím, zda si uživatel přeje vidět srovnávací metodu jako pravdu, s níž se kandidátská metoda porovnává, nebo zda za nejlepší odhad skutečné hodnoty vzorku považuje průměr obou srovnávaných metod. V prvním případě se na vodorovnou osu rozdílového grafu vynáší výsledky srovnávacího referenčního postupu měření. Tato možnost se obvykle používá k prezentaci dat získaných při validaci. V druhém případě, prezentovaném poprvé Blandem a Altmanem, jsou na vodorovné ose vyneseny průměry výsledků obou postupů měření.
V případě, že srovnávacím postupem měření je referenční postup měření se na vodorovnou osu vždy přímo vynáší jeho výsledky. Ovšem i výrobci často potřebují, například k vizualizaci dat během zaváděcí fáze vývoje testu, použít jako srovnávací postup měření ten aktuálně nejběžnější. V takovém případě se srovnávací postup měření nepovažuje za referenční a na vodorovnou osu se opět vynášejí poloviny součtů výsledků obou postupů měření, tj. kandidátského a srovnávacího.
Klinická laboratoř ale může za srovnávací postup měření použít svůj stávající postup měření a ten vydávat za „zlatý standard“, a považovat jej za referenční, třebaže tomu tak není. V takovém případě bývá cílem porovnat známé chování ověřeného stávajícího postupu měření s chováním neznámého kandidátského IVD postupu. Výsledky srovnávacího postupu měření by se pak stejně jako v případě referenčního postupu měření měly na vodorovnou osu vynášet přímo a bez úprav.
Druhý faktor volby typu rozdílového grafu představuje posouzení, zda variabilita rozdílů mezi dvěma srovnávanými postupy měření zůstává ve vydávaném rozsahu měření konstantní nebo zda je úměrná hodnotě měřené veličiny na vodorovné ose (např. koncentraci). Tabulka 1 shrnuje vztahy určené k vytváření rozdílových grafů.
Table 1. Formulas for creating difference plots adopted from [2], where xi is the result of the comparative measurement procedure for patient sample number i; yi is the result of the candidate measurement procedure for patient sample number i; (zi, di) are the resultant coordinates on the difference plot for patient sample number i. ![Formulas for creating difference plots adopted from [2], where xi is the result of the comparative measurement procedure
for patient sample number i; yi is the result of the candidate measurement procedure for patient sample number i; (zi, di)
are the resultant coordinates on the difference plot for patient sample number i.](https://www.prolekare.cz/media/cache/resolve/media_object_image_small/media/image_pdf/9981d82fdfdd9de37d78cd1719247553.jpg)
Abbreviations: SD, standard deviation; CV, coefficient of variation, and CV=SD/mean Odhad bias resp. vychýlení pomocí rozdílových grafů
V klinické laboratoři (kde postačuje N = 40) představuje dle [2] rozdílový graf optimální techniku odhadu vychýlení mezi kandidátským a srovnávacím postupem měření, nicméně vysoce závislou na specifických předpokladech, že variabilita rozdílů mezi oběma postupy měření je buď v rozsahu měření konstantní, nebo úměrná koncentraci.
Je-li chování rozdílů v rozdílových grafech konstantní, pak lze odhad vychýlení zjištěný v rozdílovém grafu vztáhnout k jakékoliv hodnotě měřené veličiny v daném intervalu měření. Naopak, mění-li se bias v průběhu vydávaného měřicího rozsahu lineárně, poskytují jedinečný odhad vychýlení pro jakoukoli hodnotu měřené veličiny pouze regresní analýzy, viz níže.
a) Konstantní SD (konstantní variabilita absolutních rozdílů):
Zjistí-li se v rozdílovém grafu absolutních rozdílů mezi oběma postupy měření, že distribuce těchto rozdílů je v celém vydávaném rozsahu měření uniformní, lze odhad vychýlení provést přímo buď pomocí jejich průměru nebo mediánu. Při verifikaci metody platí takový odhad vychýlení pro každou koncentraci v rámci měřicího rozsahu. Pro vztah s konstantními rozdíly SD platí, že se zjištěné rozdíly dají přímo použít k výpočtu vychýlení dle rovnice (5):
di = yi - xi (5)
Pro vztah s nezkresleným vertikálním rozdělením se pak odhad vychýlení vypočítá jako průměr všech takových rozdílů dle rovnice (6):
V konstantním rozdílovém vztahu se zkoseným vertikálním rozdělením se za odhad vychýlení považuje medián hodnot rozdílů.
b) Konstantní CV (proporcionální variabilita rozdílů):
Při konstantním rozložení CV lze použít průměr CV rozdílů adekvátního rozdílového grafu. V případech, kdy je v nich detekována významná šikmost, lze použít medián CV rozdílů.
Odhad bias:
Při výskytu symetrického rozdělení rozdílů (buď SD nebo CV) se tedy jako odhad vychýlení využívá jejich průměr či medián a k následnému stanovení konfidenčních intervalů (CI) výpočet standardní chyby (SE) daný rovnicí (7):
kde di je rozdíl mezi kandidátským a srovnávacím postupem měření pro každý vzorek i a d je průměr všech takových rozdílů.
Lineární regresní techniky proložení bodů v grafech přímkou (regresní analýza)
Srovnávací experiment provedený za účelem zavedení kandidátského postupu měření v klinické laboratoři nemusí vyžadovat žádné další techniky nad rámec analýzy rozdílového grafu. Pokud však některé výše uvedené předpoklady použití rozdílových grafů (konstantní SD resp. CV) splněny nejsou, pak zůstává nejlepší volbou regresní analýza. Pro výrobce provádějící validační studie je tato technika nezbytná. Mění-li se totiž bias v průběhu měřicího intervalu lineárně, jsou techniky přímého odhadu vychýlení z rozdílových grafů nevhodné. U takových datových souborů by regresní analýza měla být aplikována vždy.
Regrese je analytická technika obecně použitelná na širší rozsah situací než rozdílové grafy. Lineární regrese je matematická metoda, jejímž cílem je proložit body ilustrujícími daný datový soubor co nejlépe přímku. Pro každé rozhodování, jakou regresní techniku použít, by vždy prvním krokem mělo být přezkoumání předešlých studií preciznosti a důkladný popis typu rozložení rozdílů zprostředkované rozdílovými grafy.
Poskytne-li tedy srovnávací postup měření u vzorku (x1) výsledek 1, pak kandidátský postup měření musí u téhož vzorku v ideálním případě dát výsledek stejný (y1) tj. také 1, a stejně tak dává-li srovnávací postup měření u jiného vzorku (x2) výsledek 100, pak se také výsledek kandidátského postupu měření téhož vzorku (y2) musí rovnat 100. Statistická významnost rozdílu je následně posuzována testováním hypotéz (př. takové nulové hypotézy H0: průsečík přímky prochází na grafu bodem (0,0) a směrnice přímky je rovna 1).
Ve srovnávacích experimentech se dále často kvůli jeho citlivosti k náhodné chybě používá korelační koeficient (r). Jeho užitečnost v rámci SEKPM ale v zásadě spočívá při vyhodnocování rozsahu použitého analytického rozmezí a při volbě metody k proložení dat přímkou [1]. Korelační koeficient je bohužel také citlivý k rozsahu měření a jeho největší úskalí spočívá v často nesprávně přisuzované důležitosti zjištění jeho významné rozdílnosti od nuly. Korelační koeficient však nedokáže odhalit přítomnost ani konstantní, ani proporcionální složky systematické chyby, a proto se nehodí k posuzování potenciálních chyb kandidátského postupu měření. V této souvislosti by také neměla být uváděna jeho statistická významnost. Umocněním na druhou se stává koeficientem determinace (r2), což je zlomek rozptylu na ose y vysvětlený regresní přímkou nejmenších čtverců proloženou daty. Uplatnění r2 v regresních technikách viz též níže.
Pokyn [2] uvádí následující regresní techniky jako obzvláště vhodné pro srovnávací experiment: obyčejnou (jednoduchou) lineární regresi (OLR), regresi nejmenších vážených čtverců (WLS), dva různé typy Demingovy regrese a Passing-Bablokovu regresi.
• OLR je technika vhodná pro vztahy, v nichž se vyskytuje konstantní SD a rovnoměrné rozložení bodů ve vydávaném rozsahu měření a kde r2 > 0,95. Při splnění těchto podmínek poskytne OLR výsledky v souladu s jinými, složitějšími regresními technikami. Odhad r2 by neměl být používán jako kritérium přijetí či zamítnutí kandidátského postupu měření, ale jako indikátor síly regresní shody a základní pravidlo určující, zda je OLR přijatelná. OLR minimalizuje součet čtverců rozdílů vzdáleností bodů od proložené přímky ve vertikálním směru (osa y). Bohužel předpokládá, že pouze kandidátský postup měření je zatížen inherentní neprecizností, což v praxi není téměř nikdy pravda, neboť i srovnávací postup měření založený na vzorcích vyrobených gravimetricky ze standardního materiálu jeví trvalé nepreciznosti spojené s určením hmotnosti.
• WLS je volbou pro soubory dat s proporcionální rozdílovou variabilitou, které nesplňují základní předpoklady platné pro OLR a Demingovu regresi konstantních SD. Specifická váha známá jako regrese nejmenších čtverců konstantních CV dává každému bodu váhu nepřímo úměrnou druhé mocnině koncentrace na ose x. Úskalí této regrese spočívá v nesprávném předpokladu nulové nepreciznosti srovnávacího postupu měření a ve faktu, že pokud se osy navzájem zamění, poskytne výsledky ještě méně konzistentní než OLR.
• Demingova regrese konstantních SD je technika, která na rozdíl od OLR bere v úvahu jistou inherentní nepreciznost obou postupů měření. Je to speciální případ metody nejmenších čtverců, který umožňuje libovolný počet prediktorů a složitější chybovou strukturu. Jsou-li známy profily preciznosti obou srovnávaných postupů měření nebo je lze aproximovat z dostupných údajů, pak se tato regrese považuje za nejlepší volbu. Dokáže totiž pracovat se všemi informacemi o preciznosti závislými na postupu měření a velikosti měřené veličiny.
• Demingova regrese konstantních CV používá specifické vážení podobné jako WLS, ale body nacházející se v grafu vpravo nahoře mají menší vliv na regresní proložení přímkou než body ležící vlevo dole. Platí také předpoklad, že oba postupy měření mají určitou inherentní variabilitu, v tomto případě vyjádřenou jako CV.
• Passing-Bablokova regrese je technika vhodná nejen pro soubory dat s konstantním CV, ale i pro ty, které porušují snad všechny předpoklady požadované jinými lineárními technikami. Vyžaduje však větší velikost vzorku než kterákoliv jiná technika poskytující stejné výsledky. S ohledem na pokynem [2] navrhované velikosti souborů vzorků platné pro výrobce (N=100) a pro klinické laboratoře (N=40) jde o plnohodnotnou techniku obzvláště vhodnou pro soubory dat s konstantním CV. Při prokládání přímky daty nestanovuje žádné podmínky týkající se typu distribuce datových bodů. V podstatě kreslí středovou přímku přes data s tím, že na každé straně Passing-Bablok pásu je téměř stejný počet bodů.
Regresní rovnici získanou pomocí kterékoliv z uvedených technik lze následně použít k odhadu vychýlení mezi oběma postupy měření pro jakoukoliv hodnotu uvnitř intervalu srovnávaných měřených hodnot. Pro OLR nebo WLS, lze konfidenční intervaly CI (obvykle 95 %) tohoto odhadu vypočítat přímo.
U všech ostatních regresních technik však nelze konfidenční interval (CI) odhadu vychýlení vypočítat přímo pomocí rovnice. Pro techniky kombinující CI sklonu a průsečíku platí, že CI odhadu vychýlení se na specifické srovnávací hodnotě neurčuje v jejím vertikálním směru (osa y). K vytvoření sady dat N regresních bodů se zde používají tzv. iterační techniky a takto vytvořený soubor bodů se následně proloží regresní přímkou. Poté se provede odhad vychýlení ve vertikálním směru (podél osy y), vypočítají se střední chyby (SE) odhadu vychýlení, sklonu a průsečíku přímky a na jejich základě se stanoví CI. Pokyn [2] zmiňuje dvě vhodné iterační techniky: jackknife a bootstrap. V případě Passing-Bablokovy regrese musí být výhradně použita technika bootstrap.
Interpretace výsledků studie jako nejdůležitější část srovnávacího experimentu
Rozdíl mezi srovnávacím a kandidátským měřicím postupem může být zajímavý v celém jejich společném vydávaném rozsahu měření (vyjádřený obvykle jako směrnice), ale také třeba jen v jedné či více klinicky významných hodnotách měřené veličiny. Konfidenční interval (CI) zjištěného odhadu bias (průměrné vychýlení napříč celým rozsahem měření nebo vychýlení na specifické koncentraci) je vždy porovnáván s předem definovanými přijatelnými limity vychýlení.
Obr. 1 uvádí dle [2] hypotetické možnosti interpretace pěti různých výsledků odhadů bias včetně jejich 95% CI. Černé kruhy představují odhady bias a svislé čáry protínající kruhy jejich 95% CI.
Figure 1: Possible bias estimate outcomes adapted from [2]. ![Figure 1: Possible bias estimate outcomes adapted from [2].](https://pl-master.mdcdn.cz/media/image_pdf/74fc080d25578694fb5ab530b77954ec.jpg?version=1663247206)
Výsledky A a B ilustrují z pohledu laboratoře a jejího výsledného prohlášení vyplývajícího ze SEKPM obdobný případ, tj. že mezi kandidátským a srovnávacím postupem měření nebylo pozorováno žádné významné vychýlení. Výsledek A znamená, že 95% CI odhadu vychýlení zahrnuje i nulový rozdíl hodnot měřené veličiny. Výsledek B též leží uvnitř předem definovaného limitu přijatelnosti vychýlení, který zahrnuje nenulový odhad bias včetně jeho 95% CI. Vychýlení kandidátského postupu měření vzhledem k srovnávacímu postupu měření v obou případech splňuje kritérium jeho přijatelnosti s 95% spolehlivostí, a zjištěná vychýlení jsou přijatelná pro definovanou aplikaci.
Výsledek C představuje poněkud ambivalentní případ, kdy odhad bias sice stále ještě leží uvnitř předem definovaného limitu přijatelnosti, CI odhadu bias nikoliv. Nelze proto tvrdit, že kritéria přijatelnosti vychýlení byla splněna s 95% spolehlivostí. Vzhledem k tomu, že odhad bias je menší než nejvyšší limit jeho přijatelnosti, lze přijmout závěr, že vychýlení ještě přijatelné je, ale stejně tak může platit i alternativní závěr, že nepřijatelné procento výsledků bude mít vychýlení mimo přijatelný limit.
Výsledek D znamená případ, kdy odhadnutý bias leží mimo předem definovaný limit jeho přijatelnosti, což neplatí pro CI odhadu bias. V takovém případě posuzovaná data stále ještě nevykazují vychýlení mimo kritérium jeho přijatelnosti s 95% spolehlivostí. Překrývá-li totiž CI odhadu bias nejvyšší limit přijatelnosti vychýlení, lze stále ještě přijmout závěr, že vychýlení je ještě přijatelné. Takové prohlášení se zároveň považuje za ještě méně důvěryhodné než u výsledku C.
V případě výsledku E leží odhad vychýlení včetně jeho CI zcela mimo předem definovaný limit přijatelnosti bias. Provádění kandidátského postupu měření proto není pro definovanou aplikaci přijatelné. Není-li však zamítnutí kandidátského postupu měření z nějakého důvodu možné, může výsledek E srovnávací studie následně přimět klinickou laboratoř k úpravě referenčních intervalů. To však neplatí pro obligátně přijímané rozhodovací body klíčové pro klinické rozhodování. Mezní body stanovené na základě rozsáhlých klinických studií či klinických zkušeností nelze totiž libovolně účelově měnit.
V případě, že výrobce uskutečnil svůj srovnávací experiment kandidátského postupu měření a v rámci něho provedl svůj odhad bias, může zjištěný bias výrobce sloužit pro verifikační srovnávací experiment klinické laboratoře jako další vhodné kritérium přijatelnosti.
Stručný závěr pokynu [2]: klinické laboratoře potřebují vydávat prohlášení o bias zjištěném buď pomocí rozdílových grafů nebo regresních analýz. Namísto prostého uvádění směrnice a průsečíku doporučuje pokyn [2] uvádět popis rozsahu měření, na němž byla např. zjištěna konstantní SD, a bias uvádět v konkrétních měrných jednotkách nebo v případě popisu rozsahu měření, v němž byl zjištěn konstantní CV, v procentech. Pak platí, že bias stanovené v kterémkoli bodu klinického rozhodování, ležícím uvnitř takových vydávaných rozsahů měření, odpovídá pozorovanému bias.
Část – příklad provedení SEKPM ve zdravotnické laboratoři
Jako názorný příklad srovnávacího experimentu postačí minimalistický design respektující navíc zásadu cost-benefit. Proti pokynu [2] byl počet srovnávaných vzorků snížen na 20, čímž se současně zvýšilo riziko, že naměřené hodnoty budou mít jinou než normální distribuci. Je proto dobré vědět, že snížení počtu srovnávaných vzorků není v souladu s volbou některých doporučených regresních technik.
Měřenou veličinou v našem srovnávacím experimentu byla katalytická aktivita (μkat/L) ALT stanovená ve 20 vzorcích sér pacientů ambulantních lékařských zařízení v soukromé zdravotnické laboratoři (ZL) v předem určeném termínu. V dané ZL se běžně může provádět měření dané měřené veličiny na dvou analytických systémech stejného výrobce označených pro účely srovnání jako postupy A a B, přičemž postup A je laboratoří považován za „stávající osvědčený postup“ a postup B je k dispozici na analytickém systému s polovičním hodinovým výkonem, který v dané ZL slouží jako náhradní provoz. V obou postupech byl používán stejný princip měření, reagencie stejného výrobce v daném případě identických šarží. Vzorky byly nejprve měřeny srovnávacím postupem A, a to pouze jednou v rutinním denním provozu. Po zjištění hodnot μkat/L ALT postupem A byl proveden výběr vzorků tak, aby byl, co se týče hodnot měřené veličiny, co nejlépe pokryt obvyklý rozsah měření a se zpožděním cca 1 hodiny bylo provedeno měření stejných vzorků měřicím postupem B v jedné sérii měření.
Ke zpracování objektů datových souborů získaných během srovnávacího experimentu byl použit tabulkový SW Excel, který umožňuje nejrůznější zpracování souborů dat, mj. jejich uspořádání do tabulek a vizualizaci za účelem další volby vhodných analytických technik. Níže jsou v Tabulce 2 uvedeny hodnoty měřené veličiny (ALT v jednotkách μkat/L) získané pomocí obou srovnávaných postupů A a B.
Table 2. Reported ALT catalytic activity (μkat/L) obtained in two measurement procedures A and B 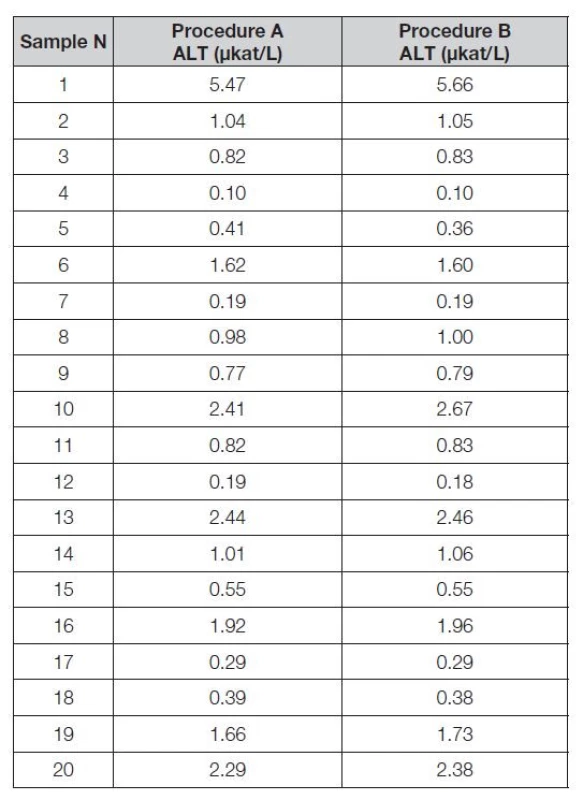
Specifikace dat
Dále je doporučeno provést popis obou získaných datových souborů, například pomocí nástroje SW Excel „Data“ → „Analýza dat“ → „Popisná statistika“ a jeho prostřednictvím zjistit, zda oba datové soubory mají normální distribuci. Je to zjištění zásadní pro vhodnou volbu dalších analytických technik. Z níže uvedených popisných charakteristik datových souborů, viz tabulka č. 3, vyplývá, že data normální (Gaussovské) rozložení nemají. V takovém případě jsou v literatuře preferovány testy neparametrické oproti parametrickým. Důležité výstupy zjištěné v rámci experimentu srovnávání jsou ve všech dalších tabulkách výrazněji šedě podbarveny.
Table 3. Summary statistics, SW MedCalc outcome 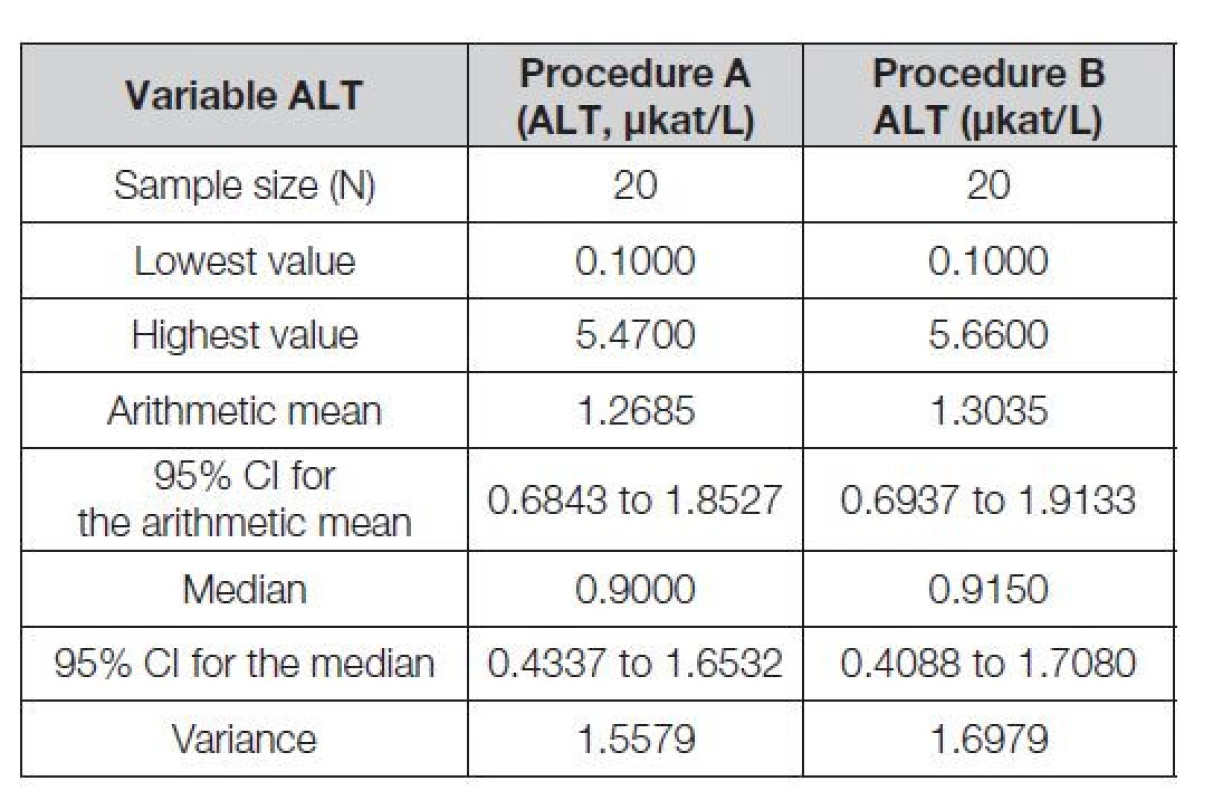
Analýza dat pomocí vhodných statistických testů
Nástroj SW Excel dále uživateli umožňuje volbu dalších vhodných testů k efektivní analýze datových souborů. F-testem o rovnosti dvou rozptylů, se příkladně ověřuje, zda dva výběrové datové soubory pochází z rozdělení se stejným rozptylem. V tomto konkrétním případě, když F < 1,0, je shoda rozptylů neprůkazná; třebaže F> f krit. (1) s pravděpodobností P ≥ 0,05, (Tabulka 4).
Table 4. F-test for variance, SW Excel outcome 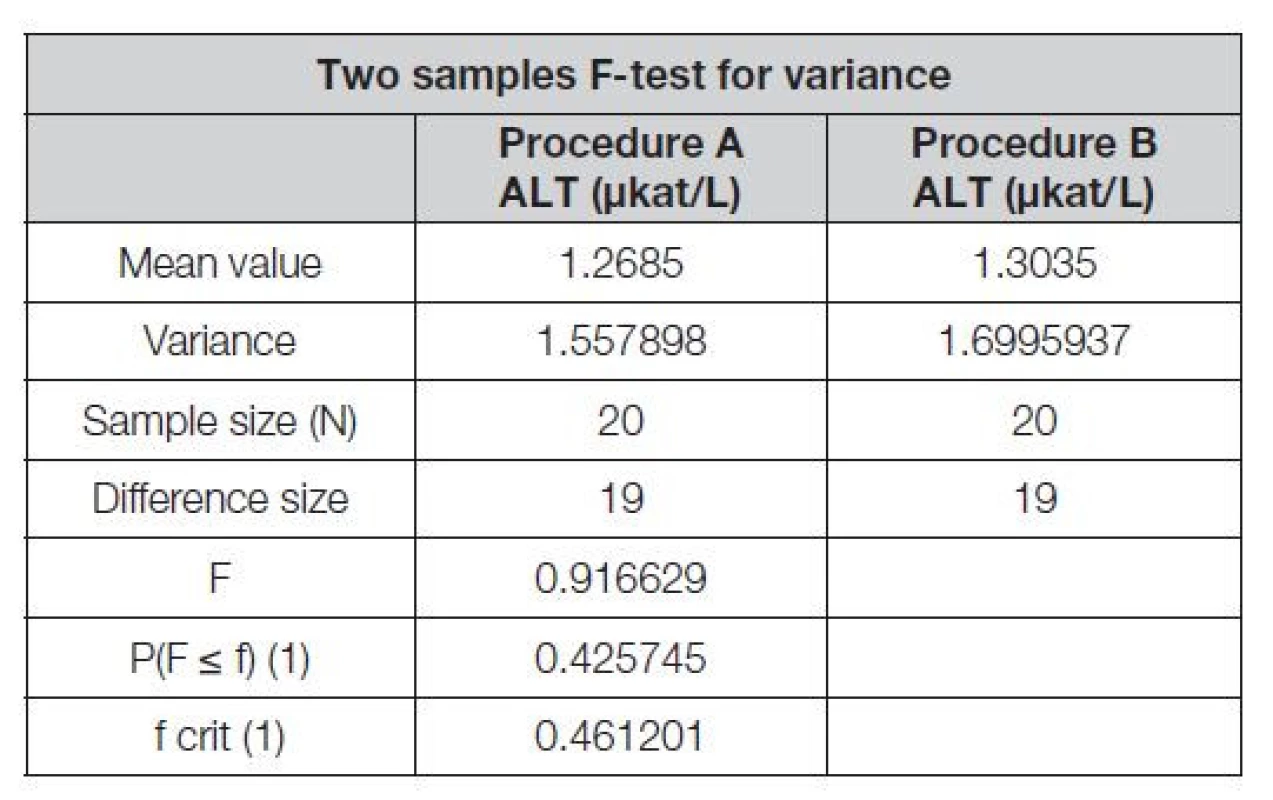
Následně byly oba datové soubory podrobeny analýze pomocí dvou různých statistických testů, a to jak parametrického (párový t-test na střední hodnotu), tak neparametrického (Wilcoxonův test). Párový t-test zde byl použit jen jako příklad. Je totiž vhodný pro data s normální distribucí, což ale pro dva výše uvedené navzájem srovnávané datové soubory neplatí, neboť podmínku normality nesplňují. Testovací statistika se počítá pomocí směrodatné odchylky diferencí sd párů měření a průměrné diference md. Tyto statistiky se uvádějí ve zprávách o srovnávacích experimentech spolu s t-statistikou, která se počítá dle rovnice (8):
kde n je počet měřených objektů.
Table 5. Two sample paired t-test of the mean, SW Excel outcome 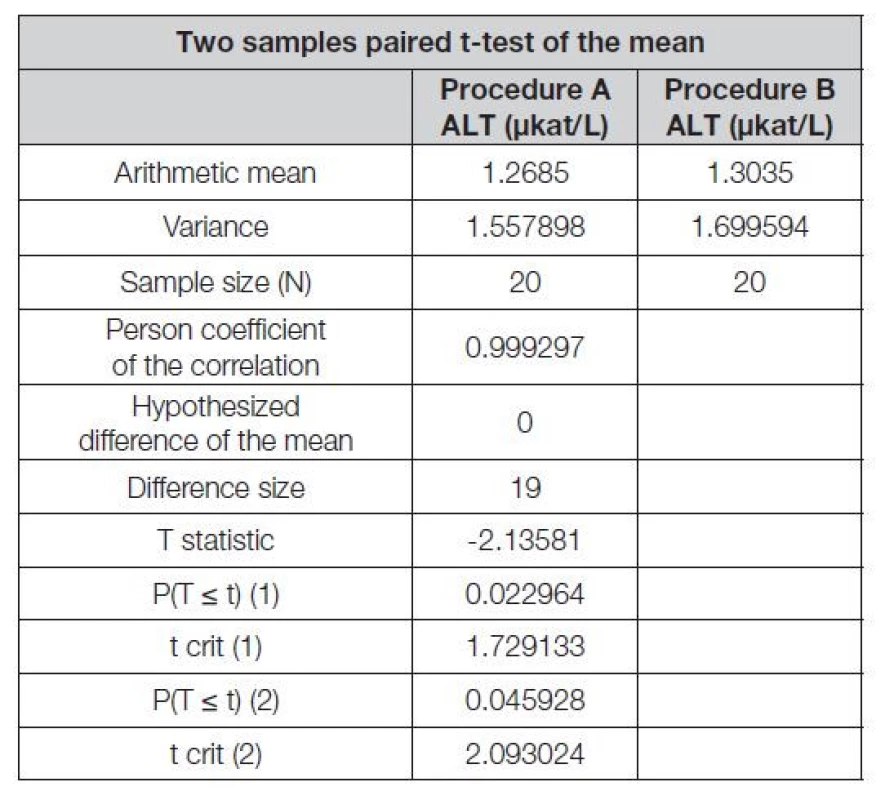
Závěr párového t-testu na střední hodnotu: T statistika > t (1) jednostranného resp. T > t (2) dvoustranného testu, a P je v obou případech ≤ 0,05. Čili na 5% hladině významnosti se zamítá nulová hypotéza H0: md = 0, tj. že průměrný rozdíl dvou datových souborů je roven 0 a přijímá se hypotéza alternativní H1: md ≠ 0, tj. že průměrný rozdíl dvou datových souborů není roven 0. Mezi oběma datovými soubory byla na zvolené hladině významnosti zjištěna párovým t-testem na střední hodnotu statisticky významná rozdílnost.
Wilcoxonův test (W-test) je pro srovnávané datové soubory, které mají jiné než normální rozložení, viz výše Tabulka 3, vhodnou a doporučenou testovací alternativou. To platí i pro naše datové soubory.
Table 6. Wilcoxon test, Analyse-it outcome, SW Excel 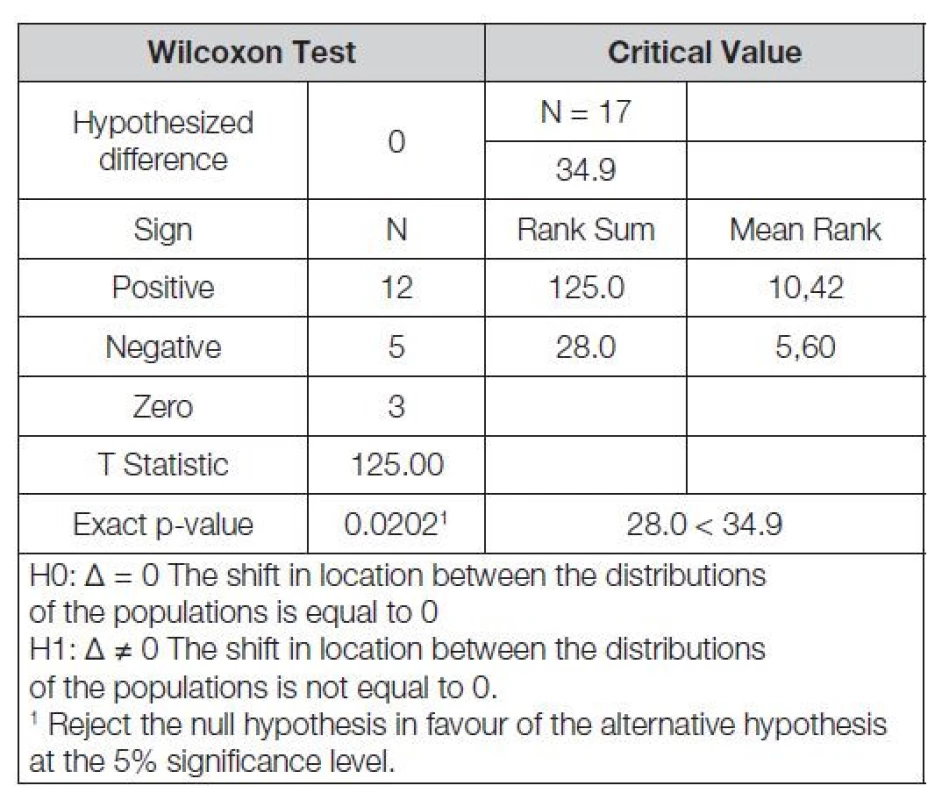
Závěr W-testu: mezi oběma datovými soubory byla na zvolené 5% hladině významnosti W-testem zjištěna statisticky významná rozdílnost. Za zmínku stojí, že neparametrický W-test poskytl v příkladové studii prakticky stejný výsledek jako parametrický párový t-test na střední hodnotu.
Vizualizace datových souborů byla provedena Bland - Altmanovým grafem, v uvedeném případě pomocí dodatku Analyse-it SW Excel. V obr. 2 je linie identity znázorněna šedou linkou a limit přijatelnosti bias přerušovanou čárou téže barvy. Rozdílový graf má své shrnutí v Tabulce 7. Na zvolené 5% hladině významnosti byla tzv. B-A fitem zamítnuta nulová hypotéza o rozdílu = 0.
Figure 2: Bland - Altman difference plot, Analyse-it outcome, SW Excel. Abbreviations: LoA, limit of acceptance. 
Table 7. Bland-Altman fit, Analyse-it outcome, SW Excel 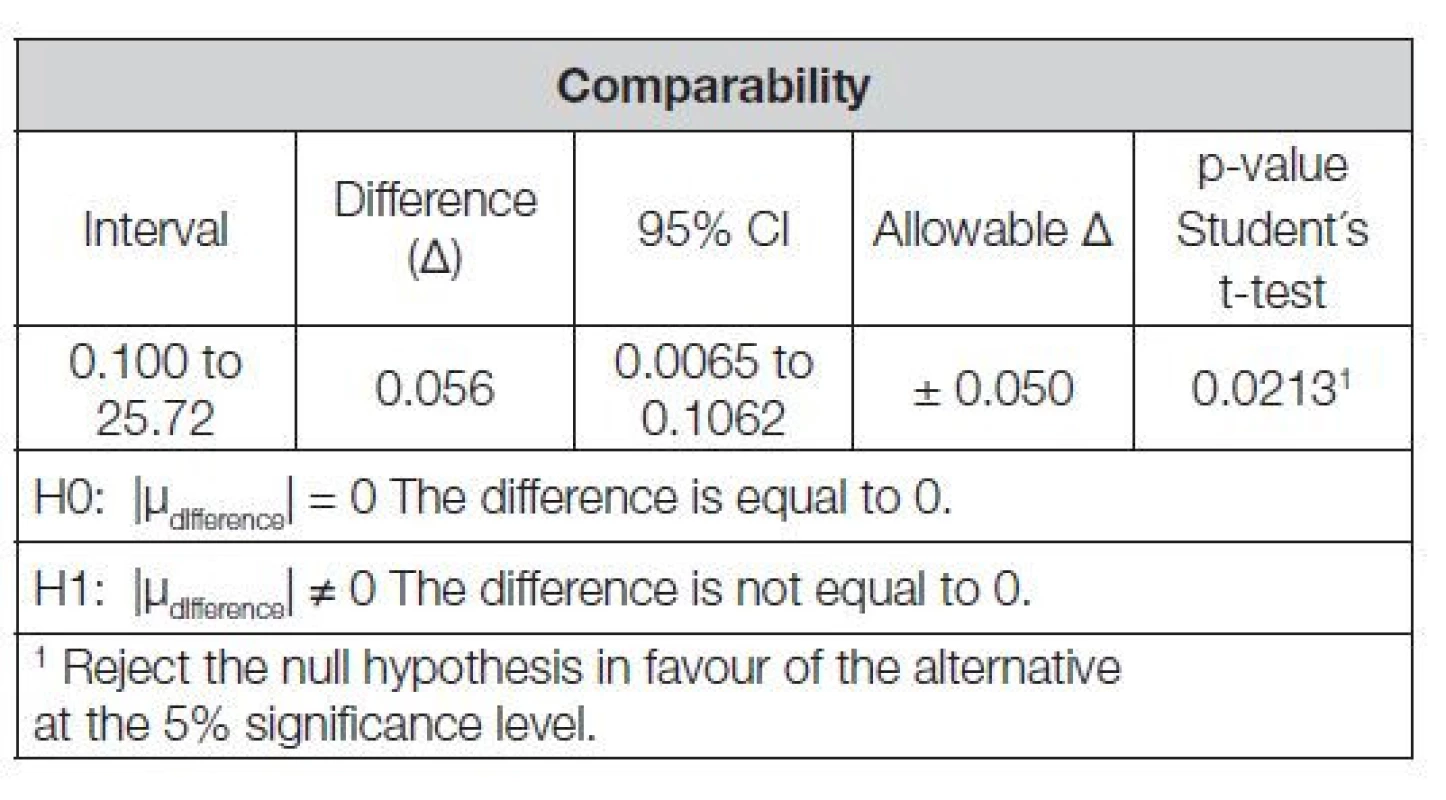
Volba regresních technik v praxi
Úvodem trocha známé teorie, v níž se praví, že ve srovnávacím experimentu jsou užitečné pouze ty statistiky, které jsou citlivé k předpokládanému typu analytické chyby [1], a výchozí model měření vyjadřuje rovnicí (9):
y = T + SE + ε (9)
kde T je naměřená resp. pravdivá hodnota, SE systematická chyba, a ε náhodná chyba s nulovou střední hodnotou a rozptylem σ. Je důležité si znovu uvědomit, že tento model lze uplatnit jak pro kandidátskou, tak pro srovnávací metodu. U systematické chyby (SE) se vždy rozlišuje konstantní složka, která je stejná v celém vydávaném rozsahu měření a proporcionální složka, která je úměrná hladině měření. Obě tyto složky mohou být způsobeny jinými mechanismy v měřícím procesu. Odhady analytických chyb pomocí parametrických testů a přidružených charakteristik se používají, pokud není přítomna proporcionální složka systematické chyby. Uvádí se pak také intervaly spolehlivosti pro průměr rozdílů a další charakteristiky.
Nejlepší odhady systematických chyb lze získat právě odhadem regresní přímky s uvedením parametrů (a, b). Testy o parametrech (a, b) regresní přímky se provádí pomocí konfidenčních intervalů (CI). Níže, v Tabulce 8, je uvedeno souhrn OLR regrese SW MedCalc, provedené na srovnávaných datových souborech; v tomto SW se regrese volí rovnicí (viz výše též Pravidlo č. 4).
Table 8. Regression y = a + bx, SW MedCalc outcome 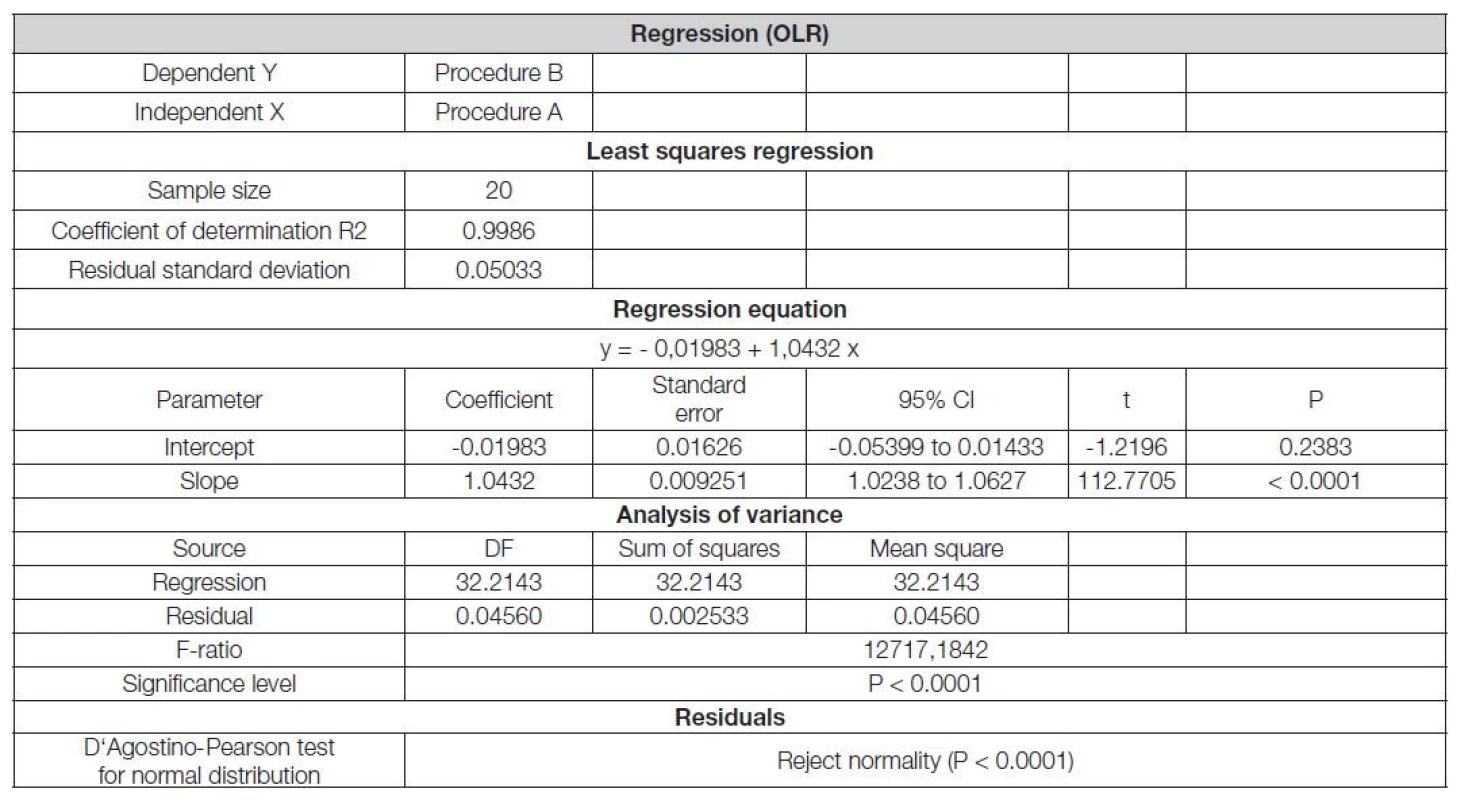
Zjištění z OLR: 95% CI průsečíku zahrnuje bod 0, což potvrzuje, že není přítomna konstantní složka SE zároveň však 95% CI směrnice nezahrnuje 1, tudíž je přítomna proporcionální složka SE. Regrese se v SW MedCalc.
Jako poslední byla na datové soubory příkladového srovnávacího experimentu aplikovaná Passing-Bablokova regrese – viz níže obr. 3, pomocí SW Analyse-it a její souhrn je uveden v Tabulce 9. Výsledky testů každého vzorku jsou na obr. 3 prezentovány jako tečky, jejichž souřadnice tvoří výsledky postupu A na ose X a postupu B na ose Y. Šedá čára představuje, identifikační čáru (linii shody), tučná černá přímka P-B regresi, tečkované čáry 95% CI P-B regrese a diagonální přerušované čáry přípustný rozdíl od identifikační čáry.
Figure 3: Passing-Bablok regression, Analyse-it outcome, SW Excel outcome 
Table 9. Passing-Bablok fit summary 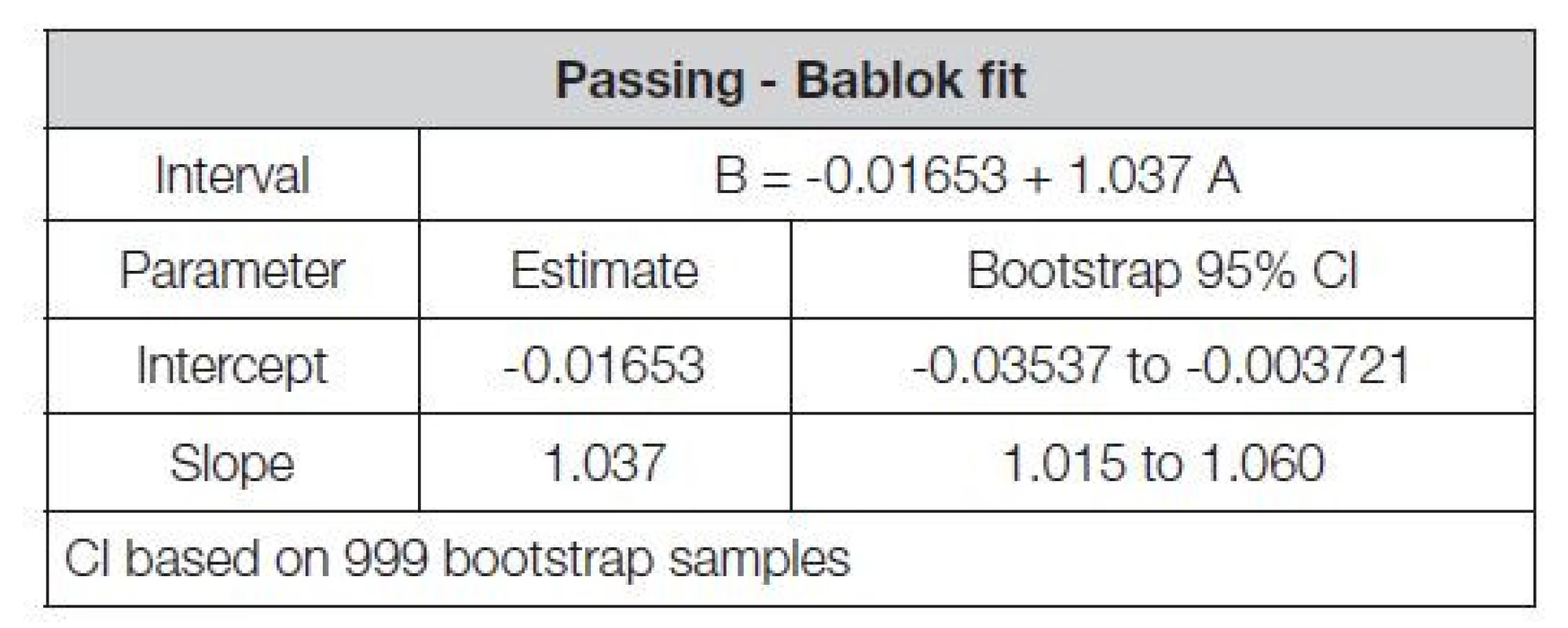
Zjištění na základě P-B regrese: 95% CI průsečíku nezahrnuje bod 0, což znamená, že je přítomna konstantní složka SE (na rozdíl od výše uvedené OLR) a zároveň 95% CI směrnice nezahrnuje 1, tudíž je přítomna proporcionální složka SE (stejně jako u OLR).
Shrnutí příkladu SEKPM: V daném srovnávacím experimentu byly zjištěny významné statistické rozdílnosti srovnávaných kvantitativních postupů měření, a to jak pomocí Bland-Altmanova rozdílového grafu, tak prostřednictvím parametrického (párový t-test na střední hodnotu) i neparametrického (Wilcoxonova) testu, a následně také pomocí dvou různých regresních technik (OLR a P-B regrese). Bylo proto nezbytné provést také srovnání obou měřicích metod postupem, který by bral v úvahu tzv. klinickou interpretační nejistotu. Za kritérium klinické přijatelnosti byl použit výpočet kritické diference (CD) na klinicky uznávané rozhodovací mezi [3,4].
CD resp. RCV (Reference Change Value) byla vypočtena na základě analytické nepreciznosti CVa (údaj převzatý z verifikace metody ALT dané ZL) a intraindividuální variability CVi (údaj převzatý z databáze biologické variability), viz Tabulka 10 dle známé rovnice (10):
CD (RCV) = 2,77 (CVa 2 + CVi 2)1/2 (10)
Table 10. Table %CD equation summary 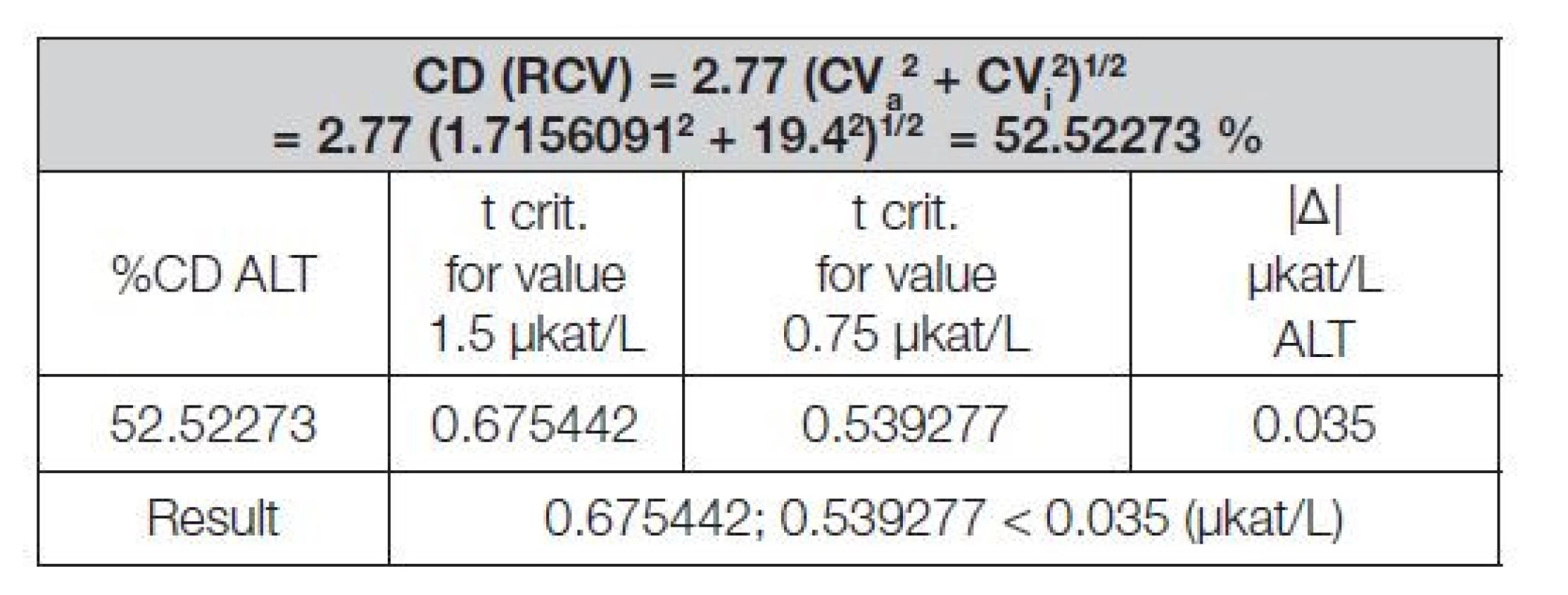
Závěr CD: Zjištěný průměrný rozdíl |Δ| dvou srovnávaných postupů měření A a B je nižší než t kritéria zjištěná na dvou zvolených hladinách katalytické aktivity ALT. Zjištěný rozdíl srovnávaných kvantitativních postupů měření byl tudíž shledán klinicky nevýznamný. Celkové shrnutí SEKPM viz Tabulka 11.
Table 11. Possible final summary outcome of the two measurement procedure comparison 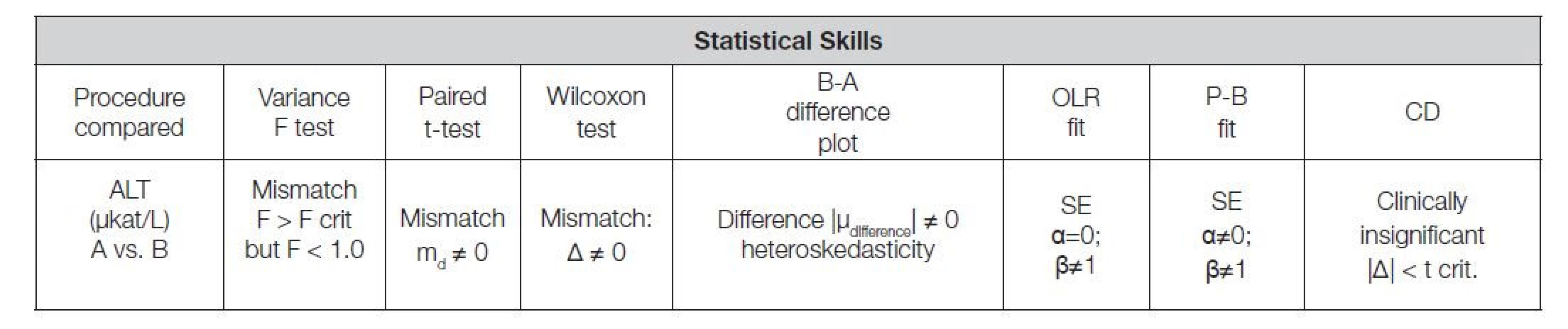
Abbreviations: B.A. Bland-Alman; P-B. Passing-Bablok; CD. Critical difference; SE = Standard error; OLR. Ordinary linear regression; md mean difference Závěr
Úkolem práce bylo dát čtenářům povědomí, že pokyn CLSI EP09c představuje metody vhodné k provádění srovnávacích experimentů kvantitativních postupů měření. Jde však o dokument obsahově poměrně rozsáhlý. Za zásadní poznání budiž přijato, že konečné prohlášení ve smyslu přijetí či nepřijetí kandidátského postupu měření vždy musí vycházet z konkrétních zjištění. jakých bylo v rámci daného srovnávacího experimentu mj. volbou vhodných statistických technik fakticky dosaženo. Je proto nezbytné srovnávací experiment nejen správně provádět, ale získané odhady rozdílů či vychýlení (bias) včetně jejich CI pak umět správně interpretovat. Totéž se týká i správné prezentace všech výsledků testování hypotéz. Většina statistických SW provádí odhad bias včetně výpočtu CI v rámci zvoleného statistického testu často společně s testováním hypotéz automaticky. Je ale důležité výsledky testů pochopit a následně řádně písemně okomentovat. A nakonec, v případě zjištění statistické významnosti rozdílů či bias, je důležité umět používat i výpočet CD jako nástroj v podstatě poslední instance resp. potenciálně nezbytné kritérium klinické přijatelnosti testovaného kandidátského postupu. A konečně mít na paměti. že v jistých specifických případech lze zjištěný rozdíl jen stěží technicky ovlivnit, což může třeba znamenat nutnost změny referenčních rozmezí.
Poděkování:
profesoru RNDr. Vlastimilu Křivanovi, CSc. za velmi podnětné připomínky Mgr. Martinu Humplovi, Abbott Laboratories ČR
Autorka prohlašuje, že není ve střetu zájmů
Do redakce došlo 19. 4. 2022
Adresa pro korespondenci
prim. MUDr. Jaroslava Ambrožová
OKB-H
Nemocnice Prachatice a.s.
Nebahovská 1015
383 01 Prachatice
e-mail: ambrozova@nempt.cz
Sources
1. Hendl, J. Statistické přístupy k porovnání biomedicínských metod měření. Česká kinantropologie 1997, 6(2), s. 87-96.
2. EP09c 3rd ed. Measurement Procedure Comparison and Bias Estimation Using Pacient Samples. CLSI June 2018.
3. Tworney, P. J. How to use difference plots in quantitative method comparison; Am Clin. Biochem., 2006, 43, 124-129.
4. Mikušková, A., Beňovská Wievorková, O., Dastych, M. Metodika a výsledky porovnání stanovení vybraných analytů na pracovištích OKB FN Brno.
5. Ricos, C., Alvarez, V., Cava, F. et al. Desirable Biological Variation database specifications; the 2014 update.
Labels
Clinical biochemistry Nuclear medicine Nutritive therapist
Article was published inClinical Biochemistry and Metabolism

2022 Issue 2-
All articles in this issue
- Editorial
- Harmonization in the clinical laboratory and the nature of external quality assessment in the near future.
- Comparability of examination results - recommended procedure
- Sborník 50. celostátního sjezdu biochemických laborantů České společnosti klinické biochemie ČLS JEP
- Abstrakta přednášek
- Abstrakta posterů
- Clinical Biochemistry and Metabolism
- Journal archive
- Current issue
- Online only
- About the journal
Most read in this issue- Comparability of examination results - recommended procedure
- Abstrakta přednášek
- Sborník 50. celostátního sjezdu biochemických laborantů České společnosti klinické biochemie ČLS JEP
- Abstrakta posterů
Login#ADS_BOTTOM_SCRIPTS#Forgotten passwordEnter the email address that you registered with. We will send you instructions on how to set a new password.
- Career









