-
Články
- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
- Kongresy
- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Statistika v biomedicínském výzkumu III
Statistics in biomedical research III
The article deals with common mistakes in data presentation, interpretation and publication. It points out the most frequent mistakes in graphic data presentation. It explains the relations between causality and correlation. It reminds of the necessity of thinking about a possible coincidence or confounding factors. It deals with the misunderstanding and misinterpretation of the p-value. It mentions publication bias which occurs when authors and editors publish mostly positive findings. It recommends researchers to contact a statistician before commencing a study.
Keywords:
data presentation – data interpretation – p-value interpretation – data publication – publication bias
Autoři: K. Langová
; J. Zapletalová; L. Ličman
Působiště autorů: Ústav lékařské biofyziky, Lékařská fakulta, Univerzita Palackého v Olomouci
Vyšlo v časopise: Anest. intenziv. Med., 28, 2017, č. 6, s. 367-370
Kategorie: Speciální článek
Souhrn
Článek se zabývá častými chybami, které jsou spojeny s prezentací, interpretací a publikací dat. Upozorňuje na nejčastější chyby při grafické prezentaci dat. Vysvětluje vztahy mezi kauzalitou a korelací, připomíná nutnost myslet i na možnou koincidenci či vliv zavádějících faktorů. Zabývá se problematikou nesprávného pochopení a špatné interpretace tzv. p-hodnoty. Upozorňuje na problém publikačního bias, který vzniká tím, že autoři a především vydavatelé časopisů publikují převážně pozitivní výsledky. Doporučuje experimentátorům kontaktovat statistika ještě před započetím studie.
klíčová slova:
prezentace dat – interpretace dat – interpretace p-hodnoty – publikace dat – publikační biasPREZENTACE
Statistické údaje prezentujeme formami textové, tabulkové nebo grafické prezentace. Textově prezentujeme statistická data v článcích především v odstavci s výsledky výzkumu. Protože textová prezentace je málo přehledná a je vhodná jen pro malý počet dat, doplňujeme ji tabulkami a grafy. Tabulkami bychom neměli čtenáře zahltit. Příliš velké množství tabulek ukazuje, že se výzkumník v datech ztratil, neumí najít správnou hierarchii, a proto uvedl vše, co měl k dispozici.
Rádi bychom upozornili i na další úskalí, kterým bychom se měli při prezentování dat vyhnout. Kvantitativní data obvykle prezentujeme pomocí statistických ukazatelů (průměru, mediánu, směrodatné odchylky, kvantilů…). Jejich správné použití bylo vysvětleno v předchozím dílu našeho statistického zamyšlení. Často se setkáváme s prezentováním kvantitativních dat pomocí sloupcových grafů s chybovými úsečkami, kde výška sloupce prezentuje průměrnou hodnotu a chybová úsečka směrodatnou odchylku, bez ohledu na typ rozdělení dat. V případě asymetrické distribuce dat je vhodné použít kvartilové box grafy, které obvykle zobrazují hodnoty mediánu, kvartilů, maxima, minima a ukazují i odlehlé či extrémní hodnoty. Na obrázku 1 vlevo je ukázka nevhodně graficky prezentovaných hodnot veličiny triacylglyceroly u mužů a žen pomocí průměrné hodnoty (výška sloupce) a hodnoty směrodatné odchylky (chybová úsečka). Rozložení této veličiny je ale zešikmené doprava, byly zde naměřeny odlehlé a extrémně vysoké hodnoty, proto je mnohem vhodnější použít ke grafické prezentaci krabicový graf (na obrázku 1 vpravo), kde vodorovná čára v krabici znázorňuje hodnotu mediánu, dolní hrana krabice hodnotu 1. kvartilu (25. percentilu), horní hrana hodnotu 3. kvartilu (75. percentilu). Anténky ukazují neodlehlé maximální a minimální naměřené hodnoty, odlehlé hodnoty jsou zakresleny kroužky a extrémní hvězdičkami.
Obr. 1. Chybné a správné grafické zobrazení distribuce veličiny triacylglyceroly u mužů a žen 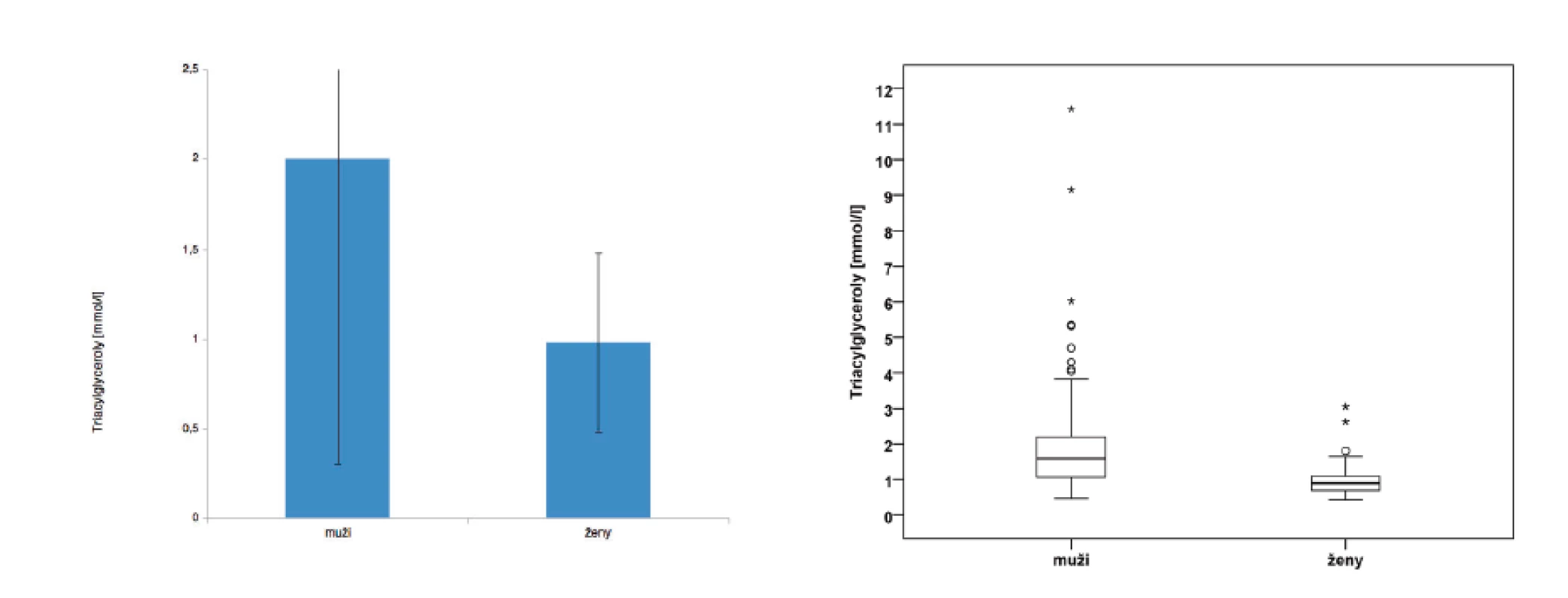
Při grafickém znázornění různými typy grafů by měly být osy grafů správně popsány a mělo by být použito správné a vhodné měřítko. Použití nevhodných měřítek na osách dokáže výsledky graficky zkreslit. Na obrázku 2 vidíte použití téhož grafu pro znázornění poklesu pravděpodobnosti přežití u pacientů s leukémií v čase. Zatímco na obrázku vlevo se pokles jeví jako mírný, na obrázku vpravo se vlivem použití odlišného měřítka na ose y zdá mnohem dramatičtější.
Obr. 2. Znázornění poklesu pravděpodobnosti přežití u pacientů s leukémií v čase 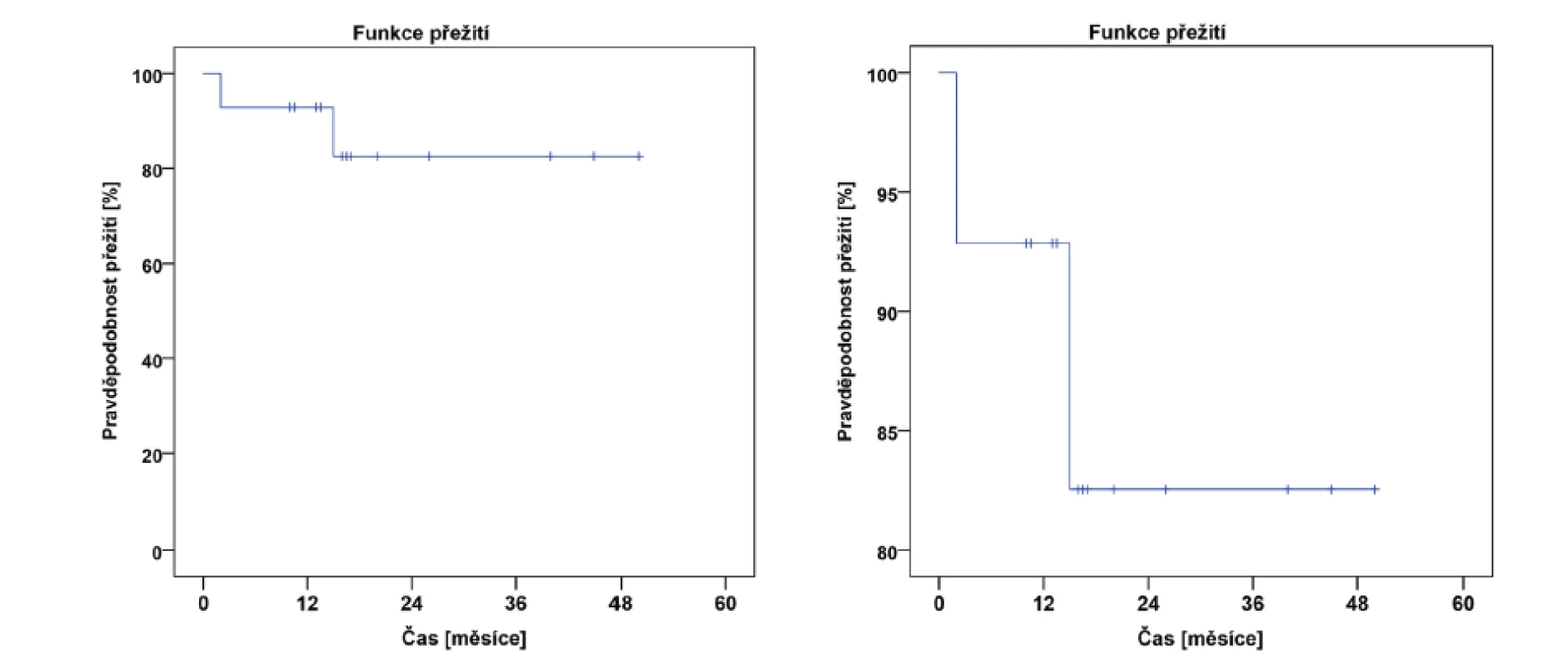
INTERPRETACE
Základní chybou je prezentovat závěry šetření, které byly provedené na vzorku populace, jen pomocí popisné statistiky bez provedení induktivní statistiky, tedy příslušných statistických testů. Pozorované rozdíly nebo závislosti mohou být jen dílem náhody a nemusejí znamenat skutečné diference nebo asociace. Naopak, v případě vyčerpávajících šetření nemá použití statistické indukce (statistických testů) žádný smysl. Cílem statistické indukce je zobecnit poznatky pozorované na vybraném vzorku z populace na celou populaci. Pokud jsou vyšetřeny všechny prvky populace, máme kompletní informaci a stačí použít metody popisné statistiky.Problematické bývá často interpretování pozorovaných vzájemných korelací mezi veličinami. Čistě statistickými způsoby nelze prokázat, zda vztah mezi veličinami je či není kauzální, testuje se pouze, zda existuje asociace (vazba) mezi zkoumanými veličinami. Pro úvahy o kauzalitě je nutno dále posoudit například časový sled, rozlišit mezi příčinami a následkem, porovnat vlastní výsledky s dosud známými fakty, posoudit konzistenci závěrů různých studií.
Ani velmi silná korelace mezi dvěma veličinami nemusí znamenat, že jedna skutečně ovlivňuje druhou. Může se jednat o koincidenci – náhodný výskyt dvou nebo více jevů či událostí, mezi kterými není zjevná souvislost. Někdy je nutné hledat tzv. zavádějící (confounding) faktory. Můžeme pozorovat asociaci mezi studovanou expozicí a následnou nemocí, která je buď částečně, nebo zcela výsledkem působení těchto „třetích“ faktorů. Příkladem může být studium vlivu pití černé kávy na riziko vzniku infarktu myokardu. Při sledování pouze pití černé kávy vyjde poměrně vysoké riziko, nicméně vesměs jde na vrub zavádějícího faktoru kouření. Jiným poměrně častým zavádějícím faktorem je sledování protektivního faktoru potravy na některá onemocnění. Například lze vysledovat velký protektivní vliv chlorofylu na vznik kolorektálního karcinomu, zavádějícím faktorem je zde vzhledem k obvyklé formě, ve které je chlorofyl přijímán, vláknina.
POCHOPENÍ A INTERPRETACE P-HODNOTY
Velkým problémem je i nesprávné pochopení a interpretace významu p-hodnoty. Interpretace p-hodnoty není vždy jednoduchá. V případě poměrně vysokých p-hodnot (řekněme > 0,2) můžeme říci, že data podobná našim bychom mohli získat poměrně často, pokud je nulová hypotéza pravdivá. Proto nemůžeme vyloučit možnost, že nulová hypotéza je pravdivá. Naopak, pokud dostaneme velmi nízké p (řekněme < 0,001), je nulová hypotéza neudržitelná, protože data podobná našim bychom dostali jen stěží náhodou, pokud by nulová hypotéza byla platná. Nulovou hypotézu v takovém případě zamítáme. Mezi těmito dvěma extrémy leží šedá zóna nejistoty, ale obvyklým postupem je zvolit si jistou mezní hodnotu α, nazývanou hladinou významnosti, a pokud je p-hodnota menší než tato mez, zamítneme nulovou hypotézu ve prospěch hypotézy alternativní. Nejčastěji je za tuto mezní hodnotu α zvolena hodnota 0,05 (5 %) [1].
P-hodnota není pravděpodobnost, že při zamítnutí nulové hypotézy děláme chybu, ani pravděpodobnost, že nulová hypotéza je pravdivá či alternativní hypotéza je nepravdivá. P-hodnota se počítá za předpokladu platnosti nulové hypotézy a neříká nám nic o platnosti alternativní hypotézy, která je obvykle předmětem našeho zájmu. Zamítnutí nulové hypotézy však ještě neznamená, že alternativní hypotéza musí být pravdivá [1].
P-hodnota nám pouze udává pravděpodobnost, že pozorujeme naše zkoumaná data nebo data ještě více extrémní (ve větším rozporu s nulovou hypotézou), když je ve skutečnosti nulová hypotéza pravdivá. Je to způsob rozhodování o výsledku testu vzhledem k předem zvolené hladině významnosti. Hladina významnosti α není dána p-hodnotou, ale je to experimentátorem volená hodnota, která by měla být stanovena před zahájením sběru dat. Obvykle volená hladina 0,05 vychází z historických konvencí, byla navržena statistikem R. A. Fisherem v roce 1925. Obecně ale neexistuje žádný důvod, proč volit právě tuto hodnotu. V mnohých publikacích již bylo upozorňováno, že takto zvolená hranice zpomaluje vědecký pokrok a má škodlivý vliv na odbornou literaturu [1].
Sám R. A. Fisher nezamýšlel používat tuto hodnotu striktně fixně. V publikaci z roku 1956 doporučil, že by hladina významnosti měla být nastavována podle specifických okolností výzkumu.
PUBLIKACE
Publikační bias
Závažným problémem je i publikační bias (předpojatost). Podstatou je to, že autoři publikují převážně pozitivní výsledky, méně pak negativní a jen výjimečně výsledky paradoxní. Pozitivní výsledek znamená, že je testovaný postup efektivnější než placebo nebo než jiný postup. Negativní výsledek znamená, že statisticky nelze zamítnout hypotézu o stejném účinku testovaného postupu a placeba, respektive jiného postupu. Paradoxní výsledek může nastat v situaci, kdy se na malé skupině dobrovolníků testuje postup, který je jen velmi málo účinný nebo je neúčinný. Při hodnocení výsledků takové studie může vlivem náhodných fluktuací dojít k tomu, že placebo vyjde jako mnohem účinnější postup, než je ten testovaný, přičemž z předchozích pozorování plyne, že testovaný postup nelze pokládat za škodlivý [3]. Publikační bias je způsoben autocenzurou výzkumníků, kteří ani neuvažují o publikaci jiných než pozitivních výsledků, a především neochotou vydavatelů odborných časopisů, kteří málokdy publikují statisticky nevýznamné výsledky. Nesignifikantní výsledky studií by měly být publikovány a neměly by být interpretovány jako negativní. Pokud zpracováváme data malých souborů, statistické testy mají nižší sílu a prokázání statisticky významných rozdílů je obtížné [2]. Na takové výsledky bychom měli nahlížet jako na neprůkazné. Publikační bias pak znehodnocuje výsledky metaanalýz, které jsou založeny na statistické kombinaci dříve publikovaných výsledků více vzájemně si podobných studií.
ZÁVĚR
Naše rada na závěr? Zamysleme se před každou studií nad tím, co chceme prokázat, proč to chceme prokázat a jakým způsobem to budeme prokazovat. To nám umožní zvolit optimální postup, vhodné statistické metody, správnou (i kritickou) prezentaci a interpretaci závěrů a úspěšnou publikaci výsledků. Pokud nejste odborníci zběhlí ve statistice, nebojte se obrátit na statistika, který se zabývá zpracováním biomedicínských dat. Nejlépe ještě před započetím studie, kdy vám statistik může pomoci i s volbou optimální velikosti souboru.
Práce je původní, nebyla publikována ani není zaslána k recenznímu řízení do jiného média.
Práce byla prezentována formou přednášky na XXV. šumperských dnech alergologie a klinické imunologie (8.–9. dubna 2016, Kouty nad Desnou).
Autoři prohlašují, že v souvislosti s tématem práce nemají střet zájmů.
Všichni autoři rukopis četli, souhlasí s jeho zněním a zasláním do redakce časopisu Anesteziologie a intenzivní medicína.
Financování: Práce byla podpořena grantovým projektem LO1304.
Do redakce došlo dne 3. 5. 2017.
Do tisku přijato dne 30. 6. 2017.
Adresa pro korespondenci:
Mgr. Kateřina Langová, Ph.D.
E-mail: katerina.langova@upol.cz
Zdroje
1. Hynek M, Zvárová J. Statistické metody v medicíně II – p-hodnota. Actual Gyn. 2016;8 : 24–25.
2. Zvárová, J. Základy statistiky pro biomedicínské obory, Praha: Karolinum; 2004.
3. Greenhalgh T. Jak pracovat s vědeckou publikací. Praha: Grada; 2003.
Štítky
Anesteziologie a resuscitace Intenzivní medicína
Článek vyšel v časopiseAnesteziologie a intenzivní medicína
Nejčtenější tento týden
2017 Číslo 6- Jak souvisí postcovidový syndrom s poškozením mozku?
- Perorální antivirotika jako vysoce efektivní nástroj prevence hospitalizací kvůli COVID-19 − otázky a odpovědi pro praxi
- Neodolpasse je bezpečný přípravek v krátkodobé léčbě bolesti
- Metamizol v léčbě různých bolestivých stavů – kazuistiky
- Léčba akutní pooperační bolesti z pohledu ortopeda
-
Všechny články tohoto čísla
- Srovnání monitorace srdečního výdeje metodou „Pulse wave transit time“ a analýzou arteriální křivky
-
Dospělý onkologický nemocný v intenzivní péči
Je již čas říci „ano, zvážíme to“ než říkat „ne“?! - Ultrazvukově asistovaná infraklavikulární pokračující blokáda brachiálního plexu
- Srdce jako zdroj systémových embolizací
- TotalTrack VLM – nová pomůcka pro obtížné zajištění dýchacích cest
- Perioperační nutrice – význam a nutnost edukace pacientů
- Statistika v biomedicínském výzkumu III
- Bezpečné podávání farmak během anesteziologické péče
- ETIKA V INTENZIVNÍ PÉČI
- Mapovitá spinální anestezie – co je příčinou?
- MUDr. Milan Poledna (1. 6. 1922 – 1. 12. 2017)
- Doporučení pro léčbu kardiálního selhání
- Pravidelná chůze znamená menší riziko smrti
-
Anestezie v Rakousko-Uhersku během I. světové války a po vzniku samostatného československého státu
Část III – Intravenózní regionální anestezie a neuroaxiální metody anestezie - Zajímavosti, tipy a triky
- Rejstříky
- Anesteziologie a intenzivní medicína
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- ETIKA V INTENZIVNÍ PÉČI
- Srdce jako zdroj systémových embolizací
- Srovnání monitorace srdečního výdeje metodou „Pulse wave transit time“ a analýzou arteriální křivky
- Ultrazvukově asistovaná infraklavikulární pokračující blokáda brachiálního plexu
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Autoři: prof. MUDr. Vladimír Palička, CSc., Dr.h.c., doc. MUDr. Václav Vyskočil, Ph.D., MUDr. Petr Kasalický, CSc., MUDr. Jan Rosa, Ing. Pavel Havlík, Ing. Jan Adam, Hana Hejnová, DiS., Jana Křenková
Autoři: MUDr. Irena Krčmová, CSc.
Autoři: MDDr. Eleonóra Ivančová, PhD., MHA
Autoři: prof. MUDr. Eva Kubala Havrdová, DrSc.
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



