THE FRACTAL DIMENSION-BASED DESCRIPTOR OF THE MICROVASCULAR PATTERN ON THE HISTOLOGICAL SECTION

Overview

The microvascular pattern in the histological section, i.e. the point-pattern composed of capillaries perpendicular to the plane of section, contains information about the three-dimensional structure of the capillary network. Histological processing is followed by the shrinkage of tissue of uncertain magnitude. In order to obtain relevant information, the scale-independent analysis is necessary. We used an approach based on the Minkowski cover of measured set. The true fractal dimension of the point pattern is obviously of zero, but the artificial result of the algorithm can be related to the complexity of shape. We fitted the log-log plot by the modified rounded ramp function and the slope of the oblique part was used as the fractal based descriptor. We demonstrated on histological samples of the heart that this fractal-based parameter has the property of scale and rotation invariance.

Keywords:

histopathology – biomedical image analysis – fractal analysis – point-pattern analysis

Introduction

Main approach to the analysis of tissues under both physiological and pathological conditions is usually based on the analysis of two-dimensional sections. Tissue processing for the histological analysis is accompanied by some artifacts including shrinkage. The magnitude of shrinkage depends on the composition of the tissue [1, 2]. Obviously, the shrinkage affects quantitative analysis of the structure of tissues.

The microvascular density, i.e., the surface density of capillaries on the two-dimensional histological section, is commonly used to description of the microvascular network. Changes of the microvascular network are associated with several pathologies including cardiovascular diseases [3], metabolic syndrome [4], and tu-mors [5].

The fractal dimension is the scale invariant descriptor by nature. There are plenty of methods of estimation of the fractal dimension in digitalized images [6]. Results of these algorithms are assumed to be scale invariant with certain limitations [7]. The estimated fractal dimension of the non-fractal object can be also noninteger. As demonstrated by Carlin [8], the result can be related to the complexity of the shape. This observation makes the fractal dimension attractive for biology because it allows to quantify irregularity of the shape by the scale-invariant manner. Unfortunately, this property can be lost [7]. Moreover, there are several terms denoted as the "fractal dimension". In this paper, the Minkowski-Bouligand fractal dimension [9] is used.

The differential box-counting algorithm is commonly used method for estimation of the fractal dimension [7]. Modification of this algorithm in order to analyze the point-pattern is straightforward and also sometimes used, but this approach has substantial disadvantages [10]. Indeed, if we tested the scale invariance of the box-counting algorithm used to analysis of the microvascular patter, but the result was unsatisfactory [11].

Instead of the regular mesh, which is probably the root of disadvantages of the box-counting algorithm, we have focused on the measurement based on the Minkowski cover [9].

Methods

The Descriptor Main derivation of the fractal dimension is described in the paper [9], we briefly recall important steps. The Minkowski cover E(ε) of a set E assumed to be the subset of the Euclidean space R2 is defined as follows:

where B_ε (x) is a ball of radius ε centered on the point x. Let |o|2 denotes the area of given object in the Euclidean space R2. The Minkowski-Bouligand dimension of the set E is defined as follows:

For estimation using finite-sized covering balls, the following linear relationship between parameters has been derived:

By their definition, balls B_ε (x) should be any geo-metric structure with diameter ε, the only one require-ment is that the closure of the ball ¯(B_ε (x) ) must be homeomorphic to the disc. In this work, squares were used. Main advantage of squares is their simplicity in digital geometry, main disadvantage is their rotational asymmetry. The disc is seemingly better due to the symmetry of their shape. Unfortunately, the errors associated with description of the disk in digital plane can lead to the worse result [12].

The log-log plot (Equation 3) describes the line only in the case of the fractal object. The finite set of points in the plane has the fractal dimension of zero by its definition. Indeed, if the diameter of the covering balls is too small or too big, the incline of the log-log plot is zero. The log-log plot has therefore the sigmoidal shape. For reasonable small diameters of covering balls, the shape of the fitting curve looks rather like the ramp. The fractal dimension-based descriptor, simply the fractal dimension, can be estimated as the oblique asymptote of the fitting function. We modified the rounded ramp function described by Lagerlöf [10]:

Lagerlöf proposed this function as possible alternative to splines. We modified the rounded ramp function in order to obtain independent parameters of shape and position. We also respected basic shape of the log-log plot (Equation 3). The result is as follows:

The oblique asymptote of the rounded ramp function can be assessed using the technique well known from the elementary calculus. Generally, the slope of the oblique asymptote (FD) is as follows:

Analytical solution of this limit is as follows:

Parameters A, B, C, D in the equations above are not necessarly from the set of real numbers. In order to keep the shape and orientation of the ramp function and with respect to the pixel-based nature of distances and areas, both A and B are greater than zero and both C and D are lesser than zero in all cases. This ensures that the estimated fractal dimension is greater than zero.

Histological samples

We used samples of the myocardial tissue harvested during the cardiac surgery. These samples were used in our previous research, informed content allows also this use. We used one sample from the left ventricle and one sample from the right ventricle.

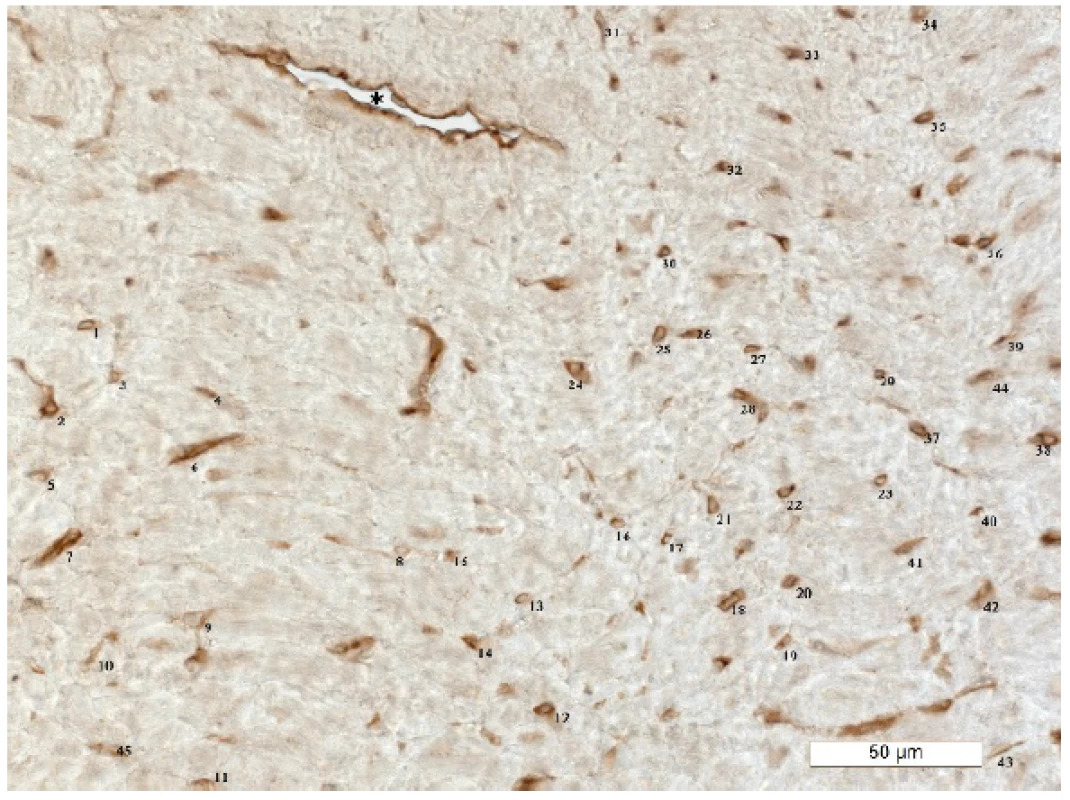
Samples of tissue were fixed in the 4% formalin, embedded into the paraffine-wax, and cut to the 5 μm thick sections. For visualization of the capillaries, immunohistochemical staining with antibodies targeted to CD31 protein was used. From each slide, one representative image under high magnification (400×) was obtained. Capillaries perpendicular to the plane of section were selected manually as the center point in the visible lumen. Example of histological staining and manual counting is on Figure 1. Files with coordinates of the center points were used for further analysis. For the analysis of the numerical stability of the algorithm, numerically scaled and rotated data were used.

Implementation and analysis

In order to calculate the covered area, we wrote the straightforward implementation of the covering in the C language (gcc 7.3.0). The coordinates of the capil-laries were used as centerpoints of boxes with sub-sequently higher and higher size. For each size of boxes, total covered area was assessed and both the covered area and diameter of the disc were used to calculate points of the log-log plot according to the Equation 3. Fitting of the log-log plot was performed in the R language (3.4.4) using the standard function nls (nonlinear least-squares). With respect to previously published works [12], we used half of the length of the shortest side of the source image as maximal length of side of the covering box. The smallest box has the length 21 pixels and the step of increase of the side of the covering boxes was 2 pixels. In the case of scaled and rotated data, the size of the image was also scaled.

We used two samples of the myocardium, the left and right ventricle. From each sample, one representative image was taken for further analysis. Numerically shrunk (scale 0.5 to 1.5, step 0.1) and rotated (from 0 to 90 degrees, 11 steps) images were used for analysis of the quality of the scale and rotational invariance.

Results

For all data, the convergence of the non-linear least square method (nls function) was obtained. In all cases, the value of all parameters of the model was significant with p-value below 0.001. Example of the fitting curve is on Figure 2.

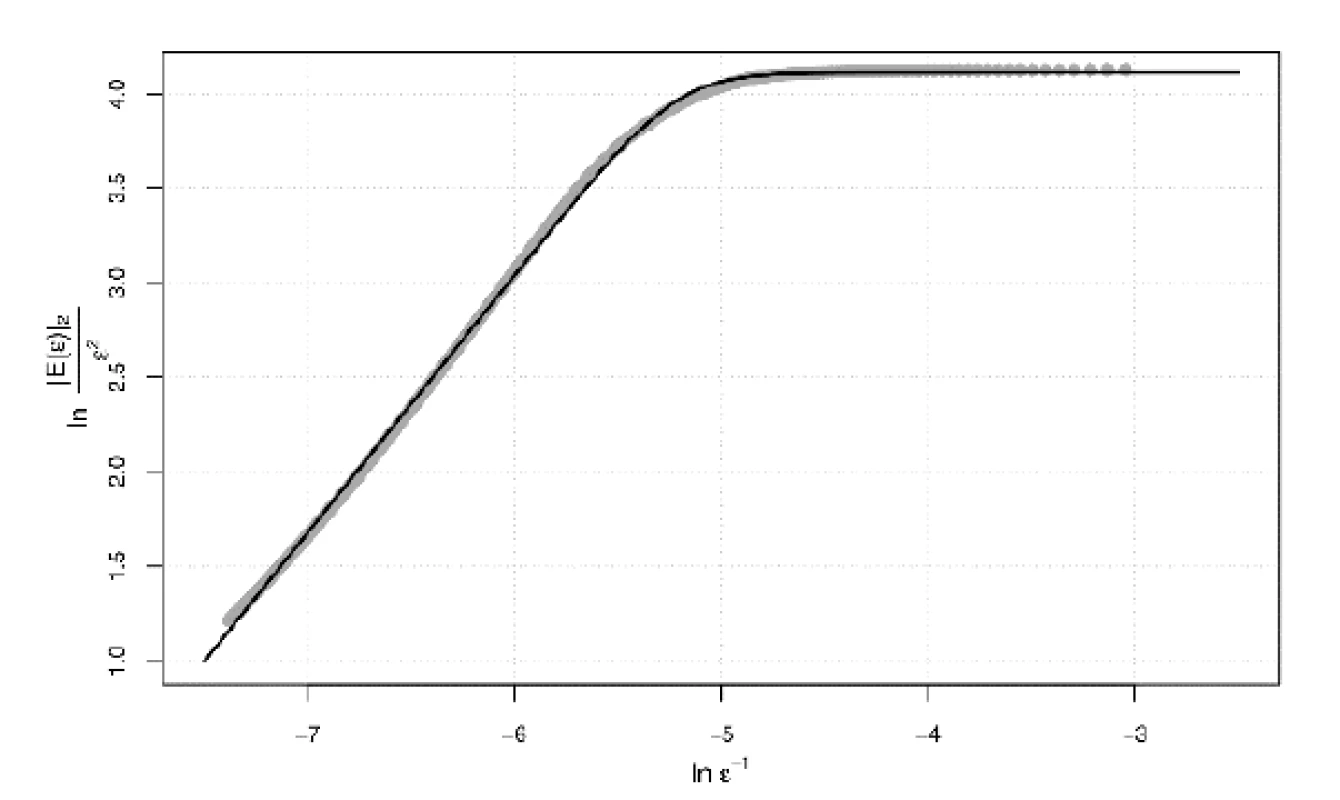
Results are summarized in Table 1 as the mean value and standard deviation. The algorithm shows very good stability with respect to the change of the scale, the variational coefficient is 0.01% for both samples. The algorithm shows good stability with respect to the rota-tion, the variational coefficient is 0.82% for the left ventricle and 0.74% for the right ventricle.

Discussion

Our approach seems to be sufficiently invariant with respect to scale and rotation. The distance of results, at least at our training samples, is sufficient to discriminate between the microvascular pattern of both samples irrespectively to the changes of the scale. This result has the biomedical importance. Scale invariance allows to compare samples obtained or processed by different ways. The assumption that the shrinkage of the tissue during the processing is homogeneous in different settings of processing of the tissue is significantly weaker than the assumption that the magnitude of the shrinkage is the same in different settings.

The advantage consisting in the scale invariance is counterbalanced by the loss of information about number of capillaries. The fractal dimension is related rather to the regularity of the distribution of the capillaries over the plane of section. This statement is related to Carlin's conclusion that the estimated "fractal dimension" is related to the complexity of the non-fractal object [8].

Conclusion

Main goal of our work was to try that the fractal-based descriptor of the point-pattern of the microvascular network on the histological section can be used as the scale invariant descriptor. Further step will be the analysis of different healthy and diseased tissues in order to detect or to compare changes in the microvascular network in the tissue during the pathogenesis.

Acknowledgement

The work has been supported by grants AZV 17-28784A and PROGRES Q25.

MUDr. Jaromír Šrámek

Institute of Histology and Embryology

1st Faculty of Medicine Charles University

Albertov 4,

CZ-128 00 Praha

E-mail: jsram@lf1.cuni.cz

Phone: +420 224 968 118