-
Medical journals
- Career
New Algorithm for EEG and EMG Separation
Authors: Jan Šebek; Radoslav Bortel
Authors‘ workplace: Dept. of Circuit Theory, Czech Technical University in Prague, Czech Republic
Published in: Lékař a technika - Clinician and Technology No. 2, 2015, 45, 43-47
Category: Original research
Overview
The paper presents newly proposed algorithm for the blind separation of EEG and EMG sources measured by high density electrode arrays. The algorithm is based on the maximization of the variance of variances of filtered principal components. Utilized high pass filter was optimized in order to extract the information which is used by the gradient algorithm to separate New Algorithm for EEG and EMG SeparationEEG and EMG components. The performance of the algorithm was evaluated by its use for the muscular artifacts removal. Present muscular artifacts were extracted from the estimated components with the use of the previously used classifier. It is compared with other similar approaches and it is shown that the suggested algorithm achieves higher quality of the processed EEG signal especially in the case of strong muscular artifacts and is therefore useful for the preprocessing of the EEG records contaminated with the muscle activity.
Keywords:
BSS, variance of variances, gradient, muscular artifacts, EMG, EEGIntroduction
This paper presents the newly proposed gradient algorithm for the blind separation of EEG and EMG sources which can be used for muscular artifacts suppression.
The distortion of EEG signals which is caused by muscular artifacts poses a serious threat to the further processing of EEG, since it can completely mask any measured EEG content. Furthermore, the conventional approaches to its removal are not always effective. The simple filtering in time or frequency is not effective because of the overlapping spectra of EEG and EMG signals and the regression filtering, which is often used for EOG artifacts removal, is not usable because of the propagation of EEG signals to the reference channel.
Algorithms using Independent Component Analysis (ICA) principle try to solve this problem by a spatial filtering principle; therefore, they are achieving better results in comparison with other techniques. Most often used algorithms in the EEG processing are FastICA [2], extended Infomax [3] and SOBI [1].
The typical ICA algorithm for muscular artifacts removal is based on four main parts [3, 4, 5]. After the necessary preprocessing, which is usually applied in order to get rid of the baseline wander and the power line disturbance, the BSS method is applied on measured EEG signals to invert the mixing process
X = AS
where the matrix A is the so-called mixing matrix, the rows of a matrix X are measured EEG signals, and the rows of a matrix S are underlying source signals. We further suppose that number of measured signals is the same as the number of sources and will be further denoted as N.
By the inversion of the mixing process, the BSS technique estimates the underlying source signals, which are of either the EEG or the artifact origin
Ŝ = WX
where the rows of a matrix Ŝ are estimated source signals, and W is the so-called demixing matrix.
The classifier is then used to select the artifactual sources [7]. The rows of the matrix containing these sources are zeroed and the EEG signal is reconstructed
Xc = W-1Ŝe
where the rows of Xc are clean EEG signals, and Ŝe denotes the matrix of the estimated source signals, where all artifactual sources were zeroed.
This algorithm should be applied on the segments of EEG with the length that is equal to the length of the present muscular artifact; otherwise, the useful information from the EEG surrounding EMG artifacts can be lost. The results presented in this paper were gained for one second long EEG segments.
The weakness that lies within this ICA approach is the necessity of sufficiently long EEG records with respect to the number of measured signals (often 8 and more seconds). If this condition is not fulfilled, the higher order statistics might not be estimated correctly and the phenomenon known as the overlearning might occur. The overlearning dramatically suppresses the capability of ICA to separate EEG and EMG sources [8], which results in the poor performance of the muscular artifacts removal algorithms.
In [8], the author uses spatial dimension reduction principle in order to suppress the overlearning within one second long EEG segments, however, the performance of these ICA algorithms tends to deteriorate with the stronger present artifacts and get close to the performance of a mere low-pass filtering applied to the measured signals [8].
Therefore, the new algorithm based on the maximization of the second order based feature is presented [8]. This estimation is not susceptible to the overlearning and can process even very short EEG segments; furthermore, it will be shown that its performance degrades more slowly in comparison with ICA for stronger artifacts.
The paper is organized as follows. The first part presents the newly proposed algorithm and its derivation. The second part gives the description of the used evaluation principle. The third part summarizes the achieved results with the algorithm and compares its performance with other used BSS methods. Finally, the advantages of the proposed algorithm are highlighted.
Methods
Proposed separation algorithm
The developed separation algorithm is based on the constrained maximization of the feature which was previously used in a control mechanism of the separation quality for the utilized FastICA algorithm [8].
As in [8], we also preprocess the input signals with the use of principal component analysis (PCA), but instead of the ICA step, we will estimate the final form of separation matrix W with the following procedure.
Let us denote N principal components by a matrix U, their filtered versions by a matrix Uf and the number of measured samples by M. We further multiply matrix Uf by a separation row vector vi, i = 1, 2, .., N to get separated components. Then the previously used checking feature, the variance of the variances of high-pass filtered components after separation, has the following form
where C is the checking feature and the function
After some algebraic manipulation, we get the following form of the checking feature
The first term in (6) is now to be maximized with respect to the separation vectors vi, i = 1, 2, .., N under the condition of their unit norm
The second term in (6) will be handled during the orthonornalization phase of the algorithm, which is also necessary as in the case of the FastICA algorithm.
For the maximization of the first term, we use the Lagrange multiplier method combined with the Newton’s method. The main goal is to determine the form of each term in
where f(vi) is the first derivative of the Lagrangia8
and J(vi) is the Jacobian matrix of form
The Lagrange multiplier λ can be derived by multiplication of (9) by viT from the left side to get
When we substitute equations (9), (10) and (11) to equation (8), we get an update step for one separation vector. In the final form of the algorithm, the separation vectors are estimated one by one following the deflation scheme of the FastICA algorithm [2]. After each update of the separation vector, the Gram-Schmidt orthonormalization is performed. The estimation stops when the separation vector change between two consecutive iterations is minimal [8]. The scheme of the proposed separation algorithm is illustrated in Fig. 1.
Fig. 1: The overall scheme of the proposed separation algorithm. 
The utilized high-pass filter should extract the maximum possible information about present muscular artifacts; therefore, the following procedure was used to determine its transfer characteristic.
The set of clean EEG signals was averaged and the PSD of result was computed and the same procedure was carried out for a set of EEG signals with strong muscular artifacts. Then the transfer characteristic of the utilized filter was determined
where S emg (Ω) denotes averaged power spectral density (PSD) of the measured EEG signal with strong muscular artifacts and S eeg (Ω) denotes averaged PSD of the measured clean EEG signals.
The estimated transfer characteristic of the utilized filter is shown in Fig. 2.
Fig. 2: The transfer characteristic of the used filter. 
Evaluation Method
To evaluate the performance of the proposed algorithm, we compared the original clean EEG signals, which are contaminated by EMG artifacts, with processed EEG signals. In order to do this, we need to have the set of clean EEG signals as well as the set of their contaminated versions.
Actually, it is impossible to measure both clean and corrupted EEG signals at the same time; therefore, we measured a set of clean EEG signals and simulated the distribution of muscular artifacts along the head's surface.
All signals were measured using the sampling frequency 1024 Hz. EEG signals were measured by the electrode system with 111 electrodes. EMG samples which were taken as muscular sources for the simulation were measured by four electrodes, two of them were placed on mandibles and the rest of them were placed on the both sides of the neck.
To simulate the distribution of muscular sources along the head's surface we used the realistic head model computed by the Boundary Element Method (BEM). Simulations were performed using a three-shell realistic head model. Each layer of this model contained 6 480 triangular elements which resulted in 19 440 elements in total. The conductivities of the brain, skull and skin regions were in ratio 1 : 1/80 : 1 [18].
The number of muscular sources in the simulation was 11, five sources represented cervical muscles and the rest of sources represented mandibles.
The simulated EMG signals were added to the clean EEG signals in the same manner as in the [9] and a set of clean EEG signals and two sets of EEG signals with variously strong muscular artifacts were created.
The performance of the proposed method was evaluated by the computation of average correlation coefficients rxy between the original clean EEG signals and the processed EEG signals for each level of EEG distortion.
Results
In the tables Tab. 1, Tab. 2, and Tab. 3, there are summarized achieved average correlation coefficients for the proposed algorithm and the FastICA algorithm with various dimension reduction strength for one second long EEG segments.
1. Correlation coefficients from processing of EEG without muscular artifacts. 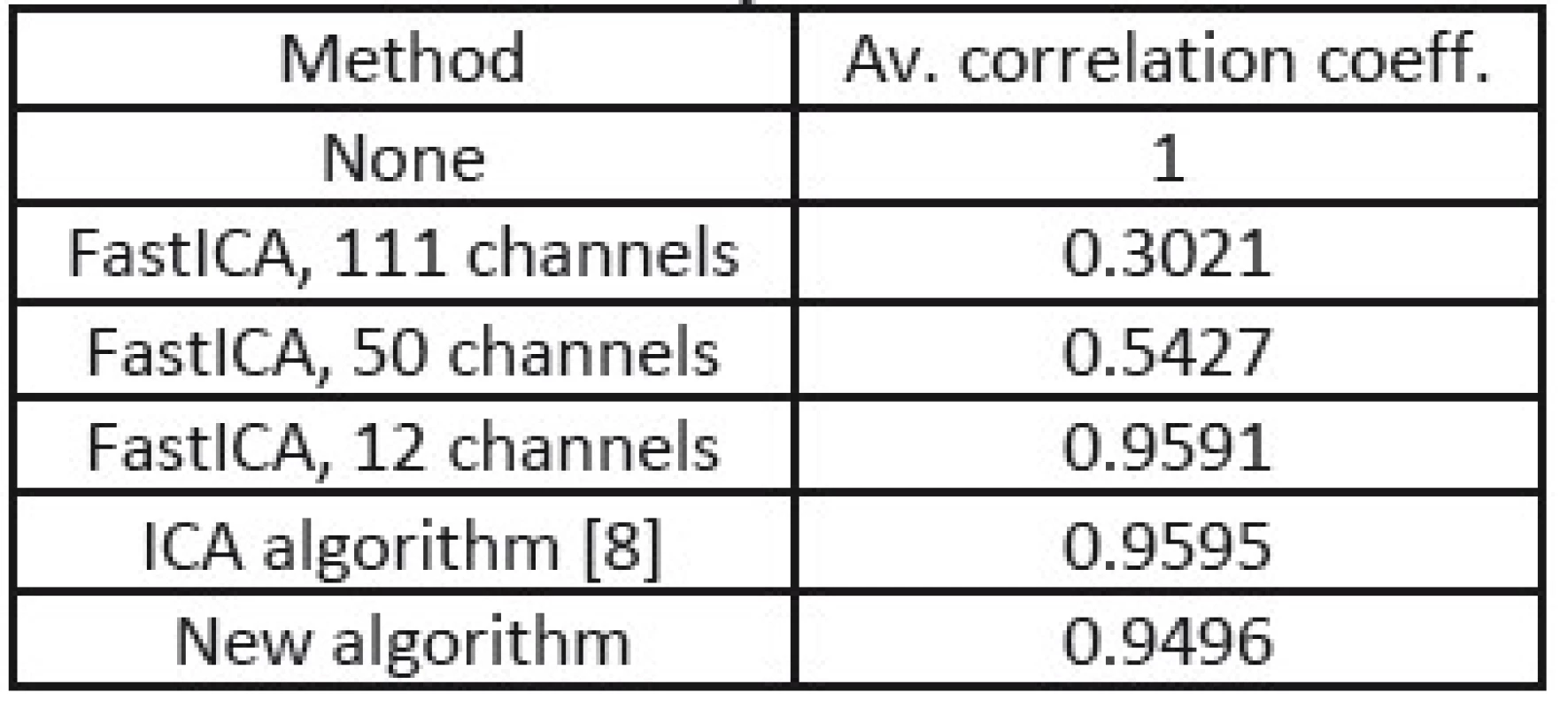
2. Correlation coefficients from processing of EEG with equally strong muscular artifacts. 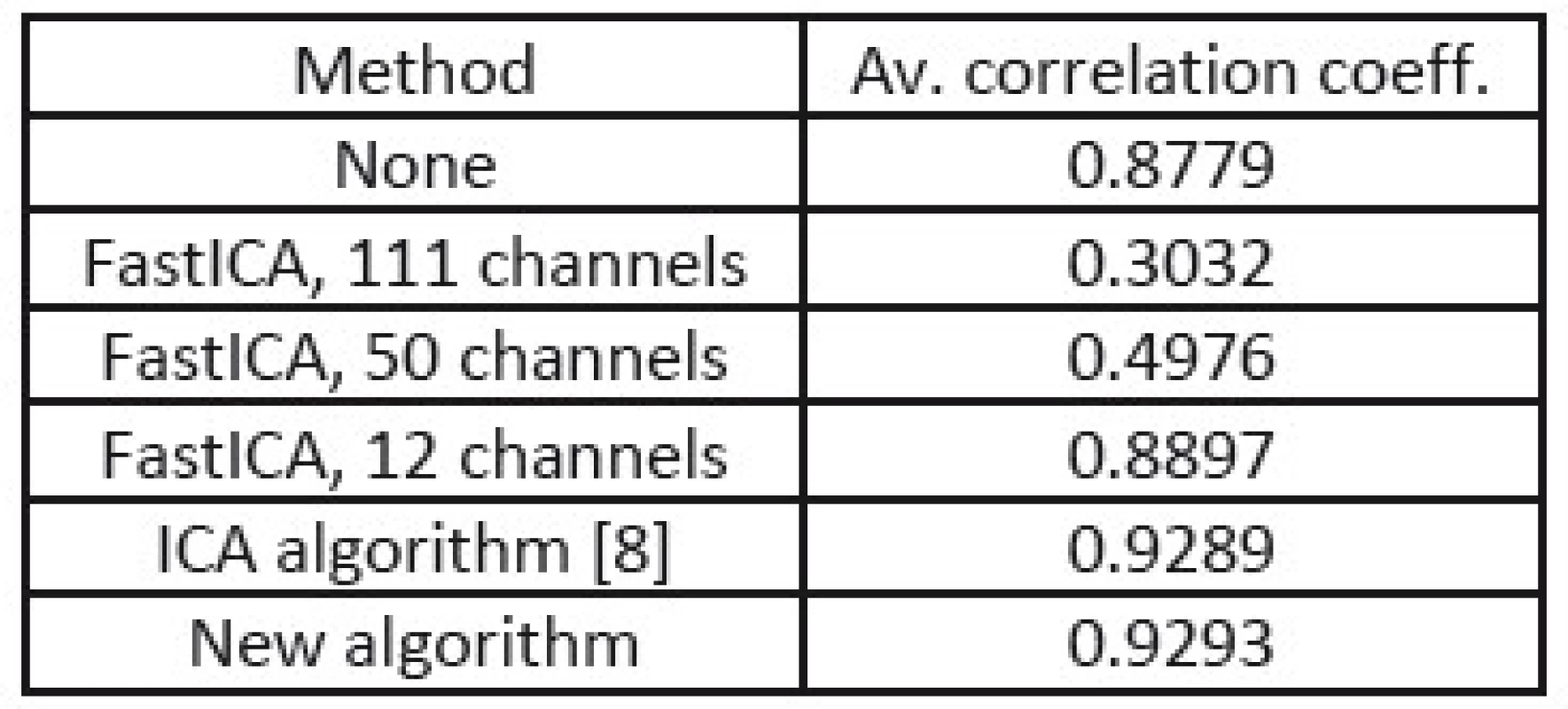
3. Correlation coefficients from processing of EEG with four times stronger muscular artifacts. 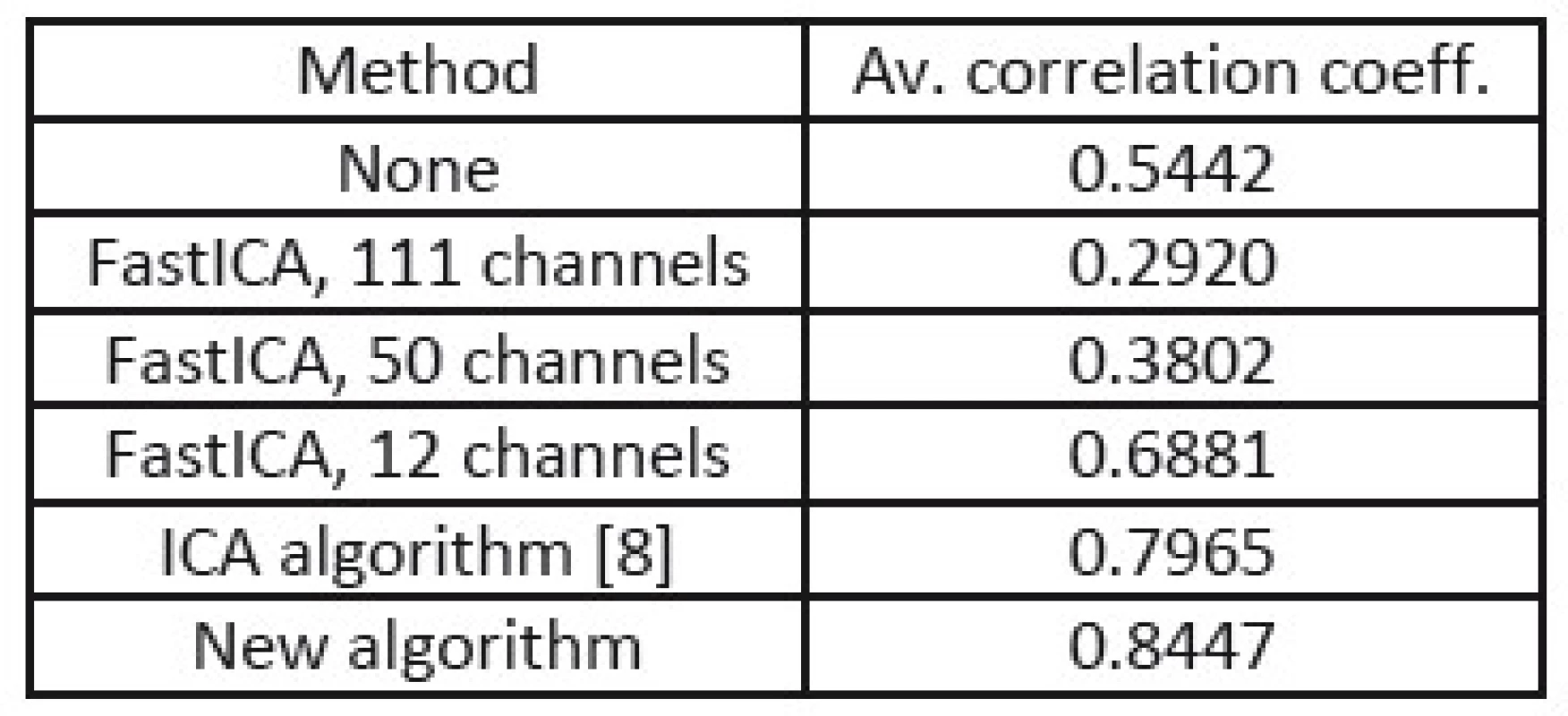
From the results in Tab. 1, 2, and 3, we can point out, that the proposed method achieved the highest value of average correlation coefficient in the cases where muscular artifacts were present in the recorded EEG. It appears that the overlearning did not occur and muscular artifacts were efficiently suppressed. In the case of the dimension reduction principle of 12 channels, the overlearning was also suppressed, but lower value of correlation indicates the greater loss of useful EEG data.
In the Fig. 3, several separated EEG and EMG components are shown indicating that the proposed algorithm successfully separated useful and artifactual contents of the measured data.
Fig. 3: a) Original measured EEG dataset with artifact. b) Several separated EEG and EMG sources. 
Acknowledgement
Research described in the paper has been supported by the Czech Student Grant Agency under grant No. SGS14/191/OHK3/3T/13.
Jan Šebek
Department of Circuit Theory
Faculty of Electrical Engineering
Czech Technical University in Prague
Technická 2, CZ-166 27 Praha 6
E-mail: sebekja4@fel.cvut.cz
Phone: +420 732 570 786
Sources
[1] BELOUCHRANI, A., ABED-MERAIM, K., CARDOSO, J.-F., MOULINES E. A Blind Source Separation Technique Using Second-Order Statistics, IEEE TRANSACTIONS ON SIGNAL PROCESSING, FEBRUARY 1997, vol. 45, no. 2, p. 434 - 444.
[2] HYVARINEN, A., OJA, E. Independent Component Analysis: algorithms and applications, Neural Networks, 2000, vol. 13, no. 4-5, p. 411-430.
[3] MAMMONE, N., MORABITO, F.C. Enhanced Automatic Artifact Detection based on Independent Component Analysis and Renyi's Entropy. Neural Networks, 2008, vol. 21, p. 1029-1040.
[4] DELORME, A., SEJNOWSKI, T., MAKEIG, S. Enhanced Detection of Artifacts in EEG Data using Higher-order Statistics and Independent Component Analysis. NeuroImage, 2007, vol. 34, p. 1443-1449.
[5] JIANWEI, W. Estimating source kurtosis directly from observation data for ICA. Signal Processing, 2011, vol. 91, p. 1150-1156.
[6] NG, S.-C., RAVEENDRAN, P. Removal of EOG artifacts using ICA regression method. IFMBE Proceedings 21 IFMBE 2008, vol. 1, p. 226-229.
[7] ŠEBEK, J., Classification of the EEG and EMG sources estimated by ICA. 17th INTERNATIONAL STUDENT CONFERENCE ON ELECTRICAL ENGINEERING, 2013, ISBN 978-80-01--05242-6.
[8] ŠEBEK, J., Metody odstraňování svalových artefaktů ze záznamů EEG. IV. Letní doktorandské dny 2014, ISBN 978-80-01-05506-9.
[9] ŠEBEK, J., Removal of Muscular Artifacts from EEG Records. 18th INTERNATIONAL STUDENT CONFERENCE ON ELECTRICAL ENGINEERING, 2014, ISBN 978-80-01-05499-4.
[10] KÁBRT, J., KÁBRT, J. LEXICON MEDICUM. 2nd ed. Galen, Praha, 2004, ISBN 80-7262-235-8.
[11] BORTEL, R., SOVKA, P. Potential approximation in realistic Laplacian computation, Clinical Neurophysiology, 2013, vol. 124, no. 3, p. 462-473.
[12] BORTEL, R., SOVKA, P. Electrode Position Scaling in Realistic Laplacian Computation. IEEE Transactions on Biomedical Engineering, 2008, vol. 55, no. 9, p. 2314 - 2316.
[13] BORTEL, R., SOVKA, P. Statistical evaluation of coherence estimated from optimally beamformed signals, Computers in Biology and Medicine, 2013, vol. 43, no. 9, p. 1286 - 1262.
[14] DELORME, A., SEJNOWSKI, T., MAKEIG, S. Enhanced detection of artifacts in EEG data using higher-order statistics and independent component analysis, NeuroImage, 2007, vol. 34, p. 1443 - 1449.
[15] BLANCO, S., GARCIA, H., QUIAN QUIROGA, R., ROMANELLI, L., ROSSO, O., A. Stationarity of the EEG series, IEEE Eng Med Biol, 1995a, vol. 14, p. 395-399.
[16] BLANKERTZ, B., TOMIOKA, R., LEMM, S., KAWANABE, M., and MULLER, K.-R. Optimizing spatial filters for robust EEG single-trial analysis, IEEE Signal Proc Magazine, 2008, vol. 25, no. 1, p. 41 - 56.
[17] SHWEDYK, E., BALUSUBRAMANIAN, R., and SCOTT, R. N. A non-stationary model for the electromyogram, IEEE Trans. Biomed. Eng, 1977, vol. BME-24, p. 417 - 424.
[18] RUSH, S., DRISCOLL, D. A. Current distribution in the brain from surface electrodes, Anesthesia and Analgesia, 1968, vol. 47, no. 6, p. 717 - 723.
Labels
Biomedicine
Article was published inThe Clinician and Technology Journal

2015 Issue 2-
All articles in this issue
- Dose Distribution Verification in stereotactc radiosurgery using radiochromic gel dosimeter
- STRUCTURED PDMS USED AS ACTIVE ELEMENT FOR A BIOMIMETICS INSPIRED FLUID TRANSPORTER
- New Algorithm for EEG and EMG Separation
- Detection of facial areas in ThERMAL IMAGES
- MODELING OF THE CHEMICAL STAGE OF RADIOBIOLOGICAL MECHANISM USING PETRI NETS
- The Clinician and Technology Journal
- Journal archive
- Current issue
- Online only
- About the journal
Most read in this issue- Dose Distribution Verification in stereotactc radiosurgery using radiochromic gel dosimeter
- STRUCTURED PDMS USED AS ACTIVE ELEMENT FOR A BIOMIMETICS INSPIRED FLUID TRANSPORTER
- New Algorithm for EEG and EMG Separation
- Detection of facial areas in ThERMAL IMAGES
Login#ADS_BOTTOM_SCRIPTS#Forgotten passwordEnter the email address that you registered with. We will send you instructions on how to set a new password.
- Career










