Respiratory Rate Estimation in Postoperative Care-State of the Art and Perspectives

Overview

In this work, respiratory rate computation based on the respiratory sinus arrhythmia is described. Based on ECG and PPG signals acquired from standard monitoring, heart rate variability was computed. After that, the respiratory sinus arrhythmia was computed filtering heart rate variability. Finally, the respiratory rate was estimated using a simple peak detection algorithm.

The benefit of the presented method is that standard monitoring, available in the recovery room, intensive care, and intermediate care, can be used. No additional sensors, such as capnography, respiration belts, or thermistors, are necessary. In future PPG imaging, a method for image-based PPG assessment, can be used as a source for the presented methods. This could permit a contactless estimation of heart rate, heart rate variability, and therefore also estimated respiratory rate.

Combining with other methods for respiratory rate estimation, such as PPG amplitude analysis or frequency analysis, can make assessment of respiratory rate more reliable. Furthermore, a combination with respiratory sinus arrhythmia based analgesia assessment can be implemented to improve pain therapy in postoperative care.

Keywords:
respiratory rate, heart rate variability, respiratory sinus arrhythmia, analgesia, ECG, PPG

Introduction

Observing a patient's respiratory rate (RR) during postoperative care, especially in the recovery room and intensive care, is very important. Changes in RR can indicate postoperative complications such as post-opioid depression [2] or arising sepsis [3]. Currently, in clinical praxis, the respiratory rate is estimated by measuring the impedance of the patient’s ECG system monitor or it is measured manually by the staff. These methods are quite imprecise. More advanced methods like capnography, respiration belts, or thermistor measurement require additional patient connections in parallel with standard monitoring. Consequently, often no reliable RR estimation is done in clinical praxis.

For RR monitoring, different approaches used previously have [4] estimated the ECG or PPG amplitude [5]. Furthermore, Bettermann et al. [6] used heart rate variability (HRV) to estimate RR based on the respiratory sinus arrhythmia. The respiratory sinus arrhythmia (RSA) is one factor that influences the HRV and is controlled by the autonomous nervous system (ANS).

HRV between 0.02 Hz and 2.6 Hz can be separated into different frequency ranges that are influenced by different physiological mechanisms. The frequency range between 0.15 Hz and 0.5 Hz is mainly associated with the RSA caused by the ANS. Lower frequencies are associated with thermo regulation. The RSA can be computed from an ECG, but the PPG is a reliable source as well [6, 7, 8].

Additionally, other physiological parameters may be derived. The analgesia nociception index (ANI), for example, uses analysis of RSA intensity leading to an index of pain sensation. This index can be used during surgical interventions and for postoperative pain assessment, e.g., pain therapy [9].

Hence, most algorithms that estimate HRV and RSA are similar, and combining ANI- and RSA-based RR estimation is obvious. In the future, an advanced patient monitor could use the ECG or PPG signal, or both, to analyze the RSA and estimate the RR and ANI. This could improve patient safety, treatment, and pain therapy during postoperative care.

Materials and Methods

Clinical trial

During a clinical trial at the University Hospital Aachen (Aachen, Germany), 44 surgical interventions were anonymously recorded using the standard operating room monitoring setup [1]. This consisted of a Philips MP70 (Philips Healthcare, Eindhoven, Netherlands) patient monitor, Draeger Primus (Draeger Medical, Luebeck, Germany) anesthesia machine, and BBraun (BBraun, Melsungen, Germany) syringe pumps. During the study, the following parameters were recorded:

• Waveform parameters from the patient monitor:ECG, PPG, and invasive blood pressure (IBP).
• Numeric values from the patient monitor: heart rate, non-invasive or invasive blood pressure, or both, and oxygen saturation.
• Waveform parameters from the anesthesia machine: CO₂ concentration and pressure.
• Numeric parameters from the anesthesia machine: end-tidal CO₂ concentration, tidal volumes, and pressures.
• Applied drugs from syringe pumps.
• Manually applied drugs.
• Important milestones, anesthesia and surgical events.

In total, 28 of 44 interventions were recorded with a CO₂ waveform signal, which was used as a reference for these datasets. Based on the CO₂ curve, RR can be easily and reliably computed. Signals were recorded during surgical interventions. Therefore, the RR was designated by the anesthesia machine. During a surgical intervention, the RR is changed only if physiological needs require change. Hence, the CO₂ signal is constant and rarely changed. Therefore, it is a good reference for the presented algorithms. In healthy patients the RSA is present, even in those who are ventilated. This fact is also used in ANI algorithms.

The ANI is not valid during application of sympathomimetic and sympatholytic drugs, because these drugs influence the ANS and the RSA. Therefore, the authors assume that RSA-based RR estimation can only be used if these drugs are not applied. This is discussed later in the information about applied drugs.

Estimation of respiratory rate from the CO₂ signal

All presented algorithms have been developed in Matlab (The MathWorks Inc., Natick, USA ) based on data recorded during clinical trials. The development, analysis and validation have been performed post-hoc. Statistical analysis was performed using SPSS statistics software (IBM, Armonk, USA)

The CO₂ signal can be assumed to be free of artifacts, except during the phase of narcosis induction and awakening of patients. Therefore, the authors used a simple algorithm to estimate the RR, determining the lower inflection point of the CO₂ curve. The algorithm entails the following steps:

• Differentiating the CO₂ signal.
• Setting the negative part of the CO₂ signal to zero.
• Using the ADAPIT [11] algorithm to estimate the peaks of the differentiated signals to retrieve the lower inflection points.
• Estimating the RR using the difference between each peak.
• Using a median filter to fair the RR signal.

The ADAPIT algorithm is designed for heart rate estimation on the ECG and PPG signal [11]. It was originally developed to be easily adaptable to the relevant signal characteristics. The algorithm is based on a sliding window where thresholds for peak detection are adapted for every data sequence. Therefore, it can easily be adapted to estimate the peaks of the differentiated signals, as described above [11].

An example signal showing the essential steps of the algorithm is seen in Figure 1.

Estimation of beat-to-beat intervals

Based on the ECG signal, beat-to-beat intervals can be estimated using different techniques. The authors used the Pan-Tompkins [10] and the ADAPIT algorithms. These algorithms can be used for real-time heart-rate estimation and beat-to-beat interval extraction. For post-hoc analysis, an adaptive peak detection algorithm was used, because it is more reliable.

The shape of the PPG signal is more smoother and the sample-rate is lower. Therefore, the detection of beat-to-beat intervals must be adapted. The ADAPIT [11] algorithm can easily be adapted. Therefore, this algorithm was used for estimating the beat-to-beat intervals from the PPG signal. Additionally, the same adaptive peak detection was compared to the ECG beat-to-beat interval estimation. In Figure 2, an example of a PPG signal with an HRV signal and filtered RSA is shown.

Elimination of extra-systoles

Hence, extra-systoles are not caused by the autonomous nervous system, and they are not related to RSA [12]. In the ANI algorithms, these extra-systoles are filtered out during preprocessing. Influence from the RR estimation can be assumed, as well. Therefore, the same algorithm was implemented [12]. Computation of RR is performed with and without extra-systole filtering to assess the effect of the filter.

Extra-systoles are detected in checking every beat-to-beat interval. If the current interval is outside of an assumed window, an extra-systole is assumed. If an extra-systole is detected, a linear interpolation is used to estimate the beat-to-beat interval without the extra systole.

Computation of the RSA based RR

The next step after estimation of beat-to-beat intervals and optional extra-systole filtering is estimating RSA. The frequencies relevant for RSA can be estimated using different filters. Bettermann et al. previously used Fourier-based filter algorithms. [6].

In this work, a wavelet-based filter was used. The same filter was implemented in the ANI algorithms [9]. According to [9], the filtered beat-to-beat intervals are separated using a db2 discrete wavelet filter. The 3rd to 5th part of the decomposition is chosen to be back-transformed. This results in a 0.15 to 0.5 Hz band pass filter.

An example of the PPG signal with estimated beat-to-beat intervals and computed RSA is shown in Figure 2. The algorithm steps are:

• Filtering using a discrete wavelet filter. The resulting signal is between 0.15 and 0.5 Hz.
• Short time sliding window moving average filter.
• Peak detection with a minimum peak distance of 0.4 s.
• Estimation of period between two peaks. This is related to the RR.
• Use of a median filter to fair the RR.

The Bettermann [6] algorithm has been implemented, as well, for comparison. Basically, the main difference is its Fourier-based filter algorithm instead of the wavelet transformation.

Results

Computation of error

For evaluation of results, the RR was computed from the CO₂ signal recorded during the study at the University Hospital Aachen, as described above. To compare the presented algorithm with the reference and the Bettermann algorithm, the authors used root-mean-square deviation (RMSD) according to Equation 1.

The RMSD regards minor fluctuations of the RSA influencing the computed RR as can be seen in Figure 3.

Respiratory rate

An example of the estimated RR is shown in Figure 3. At t+600 seconds, a change of respiratory rate from 12 to 13 can be clearly seen. The PPG and ECG RR vary from the CO₂-based RR. This is caused by multiple physiological and algorithmic influences.

Algorithmic influences depend on the precision of the beat-to-beat interval computation [13] and filter algorithm. Physiological reasons can be changes in the RSA caused by stress or applied drugs. If the intensity of the coupling is becoming low, for example, by applied sympathomimetic and sympatholytic drugs, the RR estimation can fail comparable to the ANI computation.

The RMSD has been compared with and without an extra-systole filter and between groups with and without applied sympathomimetic and sympatholytic drugs. A boxplot of the resulting RMSD values is shown in Figures 4 and 5.

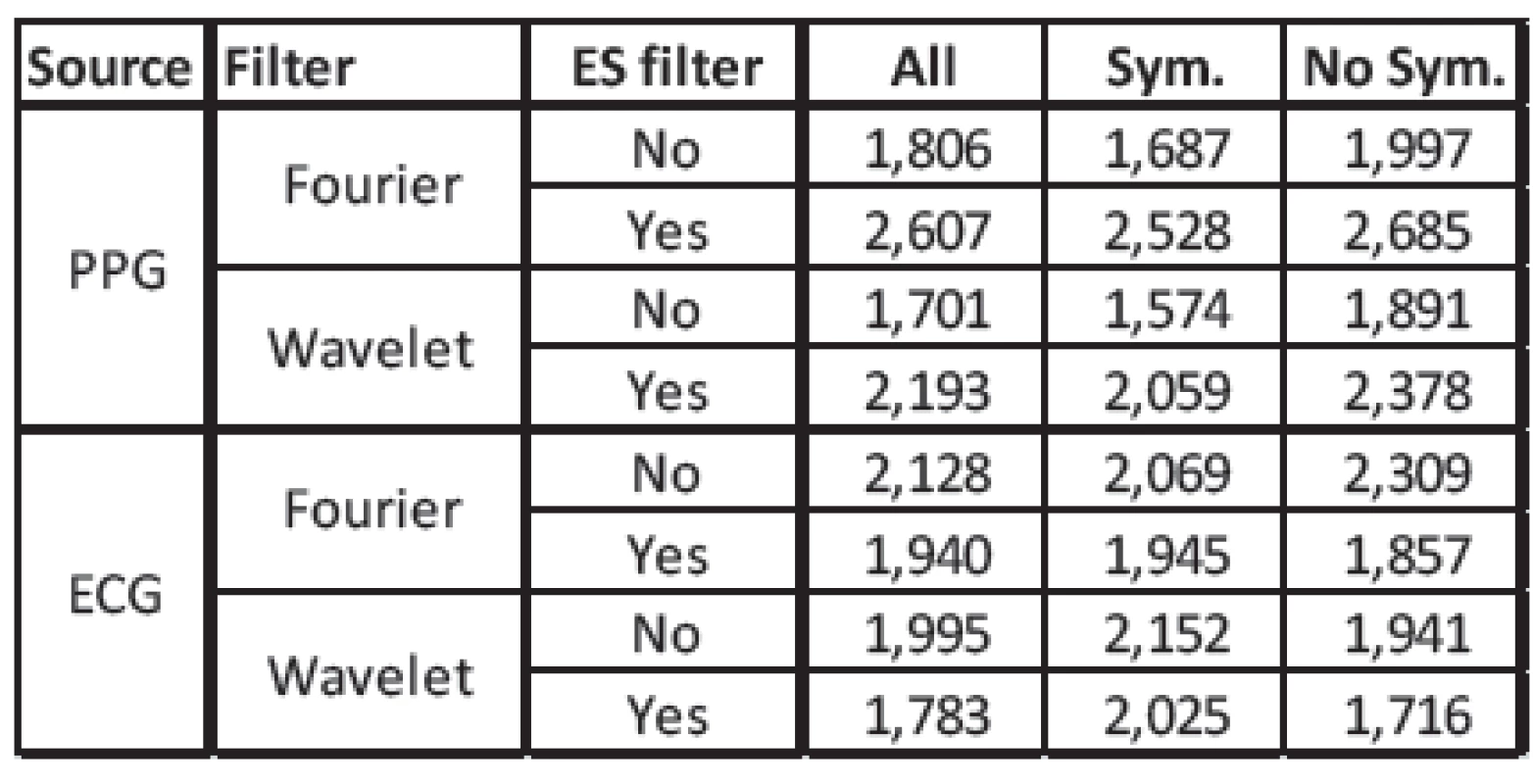
Using no extra-systole filter (Figure 4), our algorithm is comparable to the Betterman et al. algorithm, but with a somewhat smaller error. With the extra-systole filter (Figure 5), the error is lower using the ECG signal and higher using the PPG signal. In Table 1, an overview of the mean values of the RMSD is shown. An extra-systole filter would only be used if the RR is estimated on the ECG signal. Using the PPG signal, the error is heigher using the extra-systole filter. This may be caused by the influence of the measurement location. In the clinical trial, the PPG was measured using a finger clip. The beat-to-beat intervals are influenced by additional such as blood-pressure and local perufsion phenomena. Furthermore, some kinds of extra-systole have no influence of cardiac output and are not present in periferal-measured PPG.

The results of comparison between patients with symphatomimetic/symphatolytic drugs applied and those without are surprising. Although the ANI is invalid if such drugs have been applied, the error in the RR is smaller using the PPG signal. Using the ECG signal, the error is greater. The reason is that these drugs have not only an influence on the ANS but also even on blood-pressure and heart-rate, for example.

Conclusion

The presented algorithm is based on analysis of the respiratory sinus arrhythmia. The results show a comparable RMSD for our Wavelet and the Bettermann Fourier-based filter. The Wavelet-filter is more efficient, especially in combination with analgesia assessment, due to the same preprocessing.

More research should be done, analyzing the different sympathomimetic and sympatholytic drugs and the influence of RR estimation. Even the detailed influence on ANI computation should be analyzed. Maybe the influence of the different drugs can be ascertained, and the ANI can be computed even if such drugs are applied. This could improve ANI computation, as well.

Other approaches for RR estimation [14, 15] have been previously published that use the PPG amplitude or spectrum analysis of the ECG signal. In the future, these methods should be fused to make RR estimation more reliable. For example, the amplitude-based algorithms can be used to compensate for effects caused by drug delivery or patients with heart disease. Therefore, RR estimation should be switched to amplitude or frequency analysis based method.

Furthermore, RR can be computed from ECG as well from PPG signals. On the one hand, it can be used with PPG, if for example the ECG signal is not available. On the other hand, the beat-to-beat series of the ECG and PPG can be fused to compensate for artifacts, permitting a more reliable estimate of RR.

Basically, it is one of many parameters that can be derived from ECG or PPG signals. All of these algorithms have one benefit-they use vital signs, which are acquired using standard monitoring in clinical practice. Therefore, it is a useful option in order to prevent use of additional, more invasive, monitoring equipment, like capnography, thermistor measurement, or respiration belts.

The presented algorithm is especially efficient for RR estimation during clinical pain monitoring during postoperative care, because it makes use of the same preprocessing algorithms necessary for ANI computation. The differences with the Bettermann et al. algorithm are negligible.

In the future, the PPG signal may be acquired using PPG imaging (PPGI) [16, 17]. This could enable a contactless acquisition of the PPG signal, where the heart-rate, oxygen saturation, RR, and ANI can be computed wirelessly. Especially in postoperative pain therapy, this could improve patient treatment and comfort, as the patient would not need to be connected to cables.

Acknowledgement

This work is part of the OR.NET project, which is funded by the German Federal Ministry of Education and Research (BMBF).

Part of this work has been previously published under [1].

Marcus Köny, Dipl.-Ing.

Philips Chair for Medical Information Technology

Helmholtz-Institute for Biomedical Engineering

RWTH Aachen University

Aachen, Germany

E-mail: koeny@hia.rwth-aachen.de

Phone: +49 241 80 23203