THE EXACTNESS OF INTRAOCULAR LENS POWER CALCULATION FORMULAS FOR SHORT EYES AND CORRELATION BETWEEN METHOD ACCURACY AND EYEBALL AXIAL LENGTH

Overview

Purpose: To compare the accuracy of intraocular lens power calculation formulas and to examine the correlation of this exactness with the axial length for eyes shorter than 22.00 mm

Methods: The data of hyperopic patients who underwent uneventful phacoemulsification between October 2015 and June 2019 were reviewed. The intraocular lens power for each patient was calculated using 6 formulas (Holladay1, SRK/T, Hoffer Q, Holladay 2, Haigis and Barrett Universal II) before cataract surgery. Postoperative refraction was measured, and refractive prediction error was calculated 3 months after phacoemulsification. The correlation between axial length and absolute error was evaluated.

Results: Fifty-six patients (62 eyes) whose ocular axial length ranged between 20.58 mm and 21.97 mm were included in the study. The Hoffer Q formula achieved the lowest mean absolute error of 0.09 (±0.08 D). A significant correlation for the Hoffer Q (ρ = -0.329, p = 0.009) and the SRK/T (ρ = 0.321, p = 0.011) formula was observed.

Conclusions: 1. The Hoffer Q formula obtained the lowest absolute error and was recommended for intraocular lens power calculation for eyeballs with axial length shorter than 22.0 mm.

2. The correlation between axial length and absolute error is a factor which should be considered when calculating intraocular lens power. 

Keywords:

Phacoemulsification – hyperopia – intraocular lenses – Hoffer Q formula

INTRODUCTION

The exact calculation of intraocular lens (IOL) power is essential for achieving the desired refractive outcome after phacoemulsification. This is due to patients’ high expectations for precise vision after cataract surgery [1]. The exactness of implant power estimation depends not only on the accuracy of the preoperative biometric data, such as axial length (AL), keratometry (K), and anterior chamber depth (ACD), whose inaccuracy of measurement can contribute to 36%, 22%, 42% of errors, respectively [2], but most of all on the accuracy of IOL power calculation formulas. Therefore, with the development of cataract surgery, many IOL power calculation formulas have been elaborated up to their five generations [3-7].

In the 1990s, the third-generation formulas, such Sanders- Retzlaff-Kraff/Theoretical (SRK/T), Holladay 1 and Hoffer Q, remained the most widely used worldwide [8]. They all require knowledge of AL, K. However, they differ in how this information is used to calculate postoperative ACD or effective lens position [9]. The Holladay 1 and SRK/T formulas use corneal height equation, whereas the Hoffer Q formula uses an independently developed factor in which the tangent of corneal power is used [10]. The fourth-generation formulas require more parameters e.g. the Haigis formula uses K values, AL, ACD and, in addition, three constants a0, a1, a2 to calculate effective lens position (d) where d = a0 + (a1 x ACD) + (a2 x AL) [1]. In turn, the Holladay 2 formula requires 7 inputs (K values, AL, ACD, lens thickness, horizontal white-to-white, preoperative refraction and age [3]. Finally, the Barrett Universal II, as the fifth-generation formula, uses 5 parameters (AL, K, ACD, lens thickness, horizontal white-towhite [3].

We can also divide intraocular lens power calculation formulas according to the method of obtaining the results i.e. based on the observation of previous data or the optical results, which are detailed in Table 1.

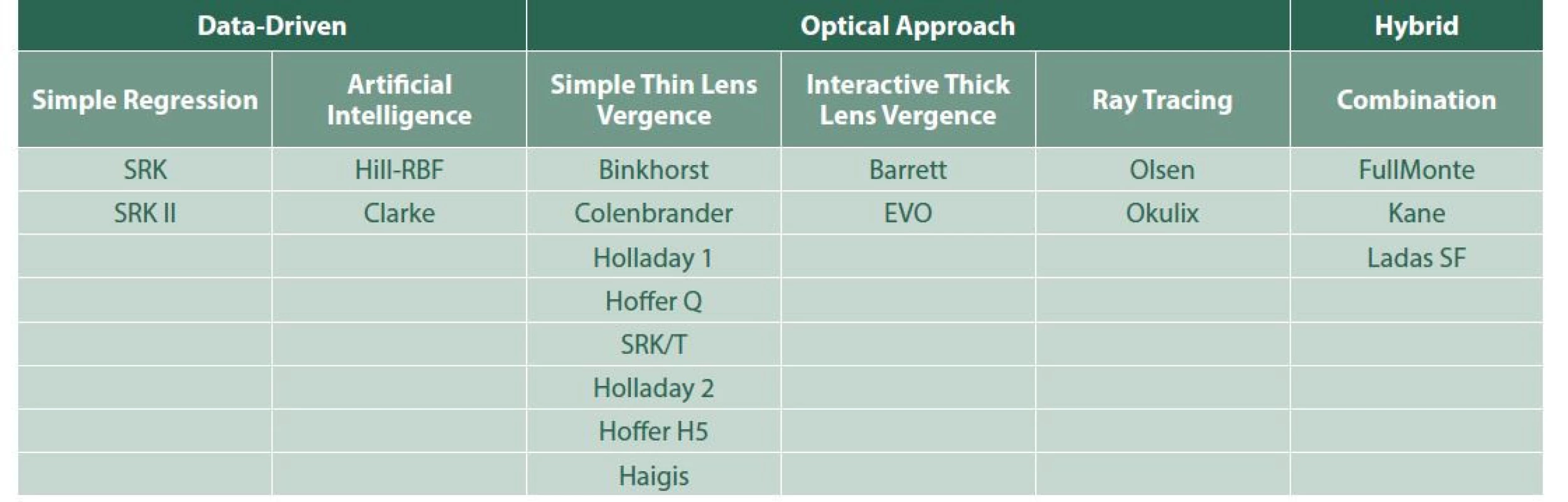
It is well known that most IOL power calculation formulas do well for eyes of AL within the 22.0 mm to 25.0 mm range [6]. The accuracy of IOL power calculation formulas for eyes shorter than 22.0 mm or longer than 25.0 mm is still questionable [11,12] despite many studies in this area.

Therefore, the aim of the study was to check the accuracy of IOL power calculation formulas for eyes with axial length not exceeding 22.0 mm. The correlation between the exactness of formula and AL was also considered, to determine when a given formula was the most accurate.

MATERIAL AND METHODS

Fifty-six patients (62 eyes), whose ocular axial length ranged between 20.58 mm and 21.97 mm with Wisconsin grade 3 or 4 cataracts, who had undergone uneventful sutureless phacoemulsification with monofocal intraocular lens implantation with 2.4 mm clear corneal incision between October 2015 and June 2019, were included in the study.

The exclusion criteria were: corneal astigmatism greater than 2.0 D or the history of other ophthalmic procedures such as vitrectomy, limbal relaxing incisions and corneal refractive surgery.

The study was conducted adhering to the tenets of the Declaration of Helsinki. Each patient signed an informed consent for a routine cataract surgery.

Preoperatively, all patients underwent a full ophthalmological examination, including the evaluation of best corrected Snellen VA, intraocular pressure measurement, anterior biomicroscopy and fundoscopy. Preoperative keratometry and ocular biometry were performed with the use of Zeiss IOLMaster 700 (Carl Zeiss Meditec AG, Jena, Germany), with partial coherence interferometry, to measure K and AL. IOL power was calculated with 6 different formulas (Holladay 1, SRK/T, Hoffer Q, Haigis, Holladay 2, Barrett Universal II), achieving theoretical postoperative emmetropia. All phacoemulsifications were performed by the same eye surgeon. Monofocal, single-piece, hydrophobic, acrylic foldable IOLs (AcrySof SA60AT, Alcon Laboratories, Fortworth, TX, USA) were implanted during the surgery. Postoperative refraction was measured 3 months after the surgery with the use of the autorefractor keratometer (Nidek ARK-1, Nidek Co Ltd, Tokyo, Japan), with at least three K measurements taken for each patient. Based on postoperative refraction results, the refractive prediction error was calculated as the difference between the real postoperative refractive outcome, expressed as spherical equivalent (the sum of spherical power and half of cylindrical power), and the residual refraction as IOLMaster outcome for the power of the IOL actually implanted, predicted by each formula. A positive value means a hyperopic prediction error and a negative value indicates a myopic prediction error, while absolute value (AV) refers to an absolute error (AE).

Statistical analysis was performed using the Statistica 13.1 package. Data were analysed, using Excel spreadsheets (Microsoft Corp). A probability of less than 5% (p < 0.05) was considered statistically significant, unless it was necessary to apply Bonferroni corrections for multiple comparisons, which reduced the significance level down to even 0.003. Data distribution for normality were checked, using the Shapiro-Wilk test. The non-parametric Kruskal-Wallis test was used to check for statistically significant differences between groups. Thereafter, the U-Mann-Whitney test for quantitative variables was used for between-pair of formula comparison. Finally, using the Spearman rank test, the correlation between AL and AE was assessed for each formula.

RESULTS

Hoffer Q, Holladay 2 and Holladay 1 formulas obtained the lowest value (-0.33 D, -0.44 D and -0.57 D respectively), while Haigis, Barrett Universal II and SRK/T achieved the highest value (-0.91 D, -0.64 D and -0.58 D, respectively) of the myopic refractive prediction error. In turn, Hoffer Q, Holladay 2 and SRK/T obtained the lowest value (0.34 D, 0.54 D and 0.63, respectively), while Haigis, Holladay 1 and Barrett Universal II achieved the highest value (0.87 D, 0.73 D and 0.71 D, respectively) of the hyperopic refractive prediction error. Only the Haigis formula obtained a greater value of the myopic than the hyperopic refractive prediction error. For the rest of the formulas, the hyperopic prediction error was greater than the myopic one.

Results of the calculated refractive prediction error are illustrated in Graph 1.

Hoffer Q, Haigis and Barrett Universal II formulas obtained the lowest value (0.06, 0.13 and 0.14, respectively), while Holladay 1, SRK/T and Holladay 2 achieved the highest value (0.23, 0.2 and 0.19, respectively) of the median of AE. Similarly Hoffer Q, Barrett Universal II and Holladay 2 formulas obtained the lowest value (0.09, 0.19 and 0.2, respectively) and Holladay 1, SRK/T and Haigis achieved the highest value (0.26, 0.23 and 0.21, respectively) of the mean AE.

Detailed AE outcomes for each formula are summarized and shown in Graph 2.

Because there was no normality data distribution, the nonparametric Kruskal-Wallis test was performed to compare AE results according to 6 formulas. As the obtained p < 0.001 outcomes were significant (probability less than 5% ), it was checked between which pairs of formulas there were statistically significant differences. Due to multiple comparisons, Bonferroni corrections were applied. Therefore the significance level was 0.05/15 = 0.003. The nonparametric U-Mann-Whitney test was performed. The Hoffer Q formula obtained the lowest level of mean absolute error of 0.09 ±0.08 D. Statistically significant differences were found in the following pairs of variables: Hoffer Q versus all other formulas, Haigis versus Holladay 1, Haigis versus Holladay 2, Barrett Universal II versus Holladay 1.

As the next step, the correlation between AE and AL was evaluated. Significant correlation factors occur between AE and AL for the Hoffer Q formula and the SRK/T formula. The first correlation shows that, with the decrease of axial eyeball length below 22.00 mm, AE increases, i.e. the accuracy of the formula decreases (correlation coefficient ρ = -0.329, p = 0.009), which is illustrated in Graph 3.

The second correlation (Graph 4) shows that, with the decrease of axial eyeball length below 22.00 mm, AE decreases as well, i.e. the accuracy of the formula increases (correlation coefficient ρ = 0.321, p = 0.011). Both correlations are low.

DISCUSSION

This study demonstrated that the Hoffer Q formula with the lowest mean AE of 0.09 is recommended for calculation of IOL power for eyeballs with AL smaller than 22.0 mm. This is similar to the study by Aristodemou et al. [4]. However, they obtained a higher mean AE of 0.46 for the LI61AO Sopfort IOL, due to as many as 66 surgeons having performed phacoemulsification. For this reason, postoperative refractive error could result not only from the low accuracy of the IOL power calculation formula, but also from the imperfection of the operating technique.

Gökce et al. showed no statistically significant differences in the mean AE between 7 formulas (Hoffer Q, Holladay 1, Haigis, Holladay 2, Olsen, Barrett Universal II and Hill-RBF) [13]. When studying the accuracy of IOL power calculation formulas for eyeballs with axial length not exceeding 22.0 mm, they obtained the lowest mean AE of 0.37 for the Hill-RBF formula and the highest mean AE of 0.42 for the Haigis formula, while it was 0.4 for the Hoffer Q formula [13]. However, significantly, the Hoffer Q formula scored the smallest range of postoperative refractive error in both the current study and theirs (0.67 D and 2.03 D, respectively) and the Haigis formula the largest range (1.78 D and 2.48 D, respectively).

Doshi et al. proved no statistically significant differences in the mean AE of Hoffer Q, Holladay 1 and SRK/T formulas [21]. They obtained much higher mean AE values i.e. 0.59 D, 0.57 D and 0.54 D, respectively, compared to the current study i.e. 0.09 D, 0.26 D and 0.23 D, respectively. However, they used the immersion ultrasound technique to obtain AL values, which is a less accurate method than using IOLMaster [21].

Carifi et al. did not observe any statistically significant differences in the mean AE of Hoffer Q, Holladay 1, Haigis and Holladay 2 formulas [14]. They studied extremely short eyeballs with very powerful IOL (range of powers +35.0 D to +40.0 D). They therefore obtained a high mean AE value of 0.95 D. In addition, they involved only 28 eyes in their study. For this reason, the results could be unreliable.

The issue of correlation was not often considered in terms of the accuracy of IOL power calculation formulas. This is more frequently studied for myopic eyeballs, where the range of lengths is much greater. Chen et al. proved that, for SRK/T and Hoffer Q formulas, a 1 mm increase in AL increased the AE by about 0.1 D when AL > 26 mm, while, in the case of AL > 33 mm, a 1 mm increase in AL increased the AE by as much as approx. 1.1 D [22].

The authors’ study showed a significant correlation between AE and AL for Hoffer Q and SRK/T formulas. With the decrease of axial AL below 22.00 mm, AE increases, i.e. the accuracy of the Hoffer Q formula decreases. Aristodemou et al. observed a similar relationship i.e. for the Akreos Fit IOL, mean AE value for the Hoffer Q formula was 0.5 D, 0.55 D and 0.76 D, when AL was 21.5–21.99 mm, 20.0–21.49 mm and 20.0–20.99 mm, respectively [4]. However, in their study, for the LI61AO Sopfort IOL, mean AE value was 0.46 D for each eyeball length in the range of 20.0–21.99 mm [4]. However, for this implant for the SRK/T formula, the mean AE value depended on the AL i.e. 0.46 D, 0.57 D, 0.75 D when AL was 21.5–21.99 mm, 20.0–21.49 mm and 20.0–20.99 mm, respectively. This correlation completely differs from that in the author’s study, in which, with the decrease of axial eyeball length below 22.00 mm, AE also decreases, i.e. the accuracy of the SRK/T formula increases. This is possibly due to a 3-piece IOL with a silicone aspheric optic in Aristodemou’s study, while single-piece, hydrophobic, acrylic foldable IOLs were used in the author’s study. It is well known that the SRK/T formula is more accurate when calculating the implant power for long eyeballs [4,21,23].

Similarly, to Chen, the author’s study showed that, with an increase of AL by 1 mm, AE increases by 0.1 D. However, the difference is that the range of AL is between 20.0 mm and 22.0 mm and the correlation applies to the SRK/T formula. For the Hoffer Q formula, this study proved that, with an increase of AL by 1 mm in the range between 20.0 mm and 22.0 mm, AE decreases by 0.1 D [22].

A limitation of this study is the relatively small length range of the operated eyeballs (from 20.58 mm to 21.97 mm). Aristodemou et al. obtained different mean AE results for certain length ranges. Thus, the Holladay 1 formula achieved the smallest mean AE for eyeballs with a length of 20.00–20.99 mm, the Hoffer Q formula of 21.00–21.49 mm and the SRK/T formula of 21.50– 21.99 mm (0.67, 0.50 and 0.43, respectively) [4]. In the author’s study, the median length of operated eyeballs was 21.49 mm, which could have resulted in the Hoffer Q formula obtaining the highest accuracy in terms of AE.

The number of studied eyeballs is the second limitation of this study. Although the group of patients does not seem large, there are many published papers where the number of patients was even smaller. Cook et al., as well as Gavin et al. studied 41 eyes [3,24], Wang et al. 33 [1], Carifi et al. 28 [14] and Roh et al. only 25 eyes [17]. On the other hand, there have been studies with more eyes – Aristodemou et al. 457 [4], Gökce et al. 86 [13], Eom et al. 75 eyes involved [25].

Another limitation of this study is that 6 patients participating in this study had both eyes operated on. However, this is only 10% of the operated eyes and should not affect the final result. In addition, all patients had the same model of IOL implanted, so these results may not be generalisable to IOL models of a different design, which may be a further limitation of the study.

CONCLUSIONS

The Hoffer Q formula obtaining the lowest AE is recommended for IOL power calculation for eyeballs with an axial length smaller than 22.0 mm.

The demonstrated positive correlation between AE and AL suggests that the exactness of the IOL power calculation formula depends on AL, which should be considered especially for extremely short eyeballs.

The author declares that he has no conflict of interest. This study received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Received: 11 April 2022

Accepted: 27 July 2022

Wiktor Stopyra, MD, PhD

MW med Eye Centre

Ul. Dobrego Pasterza 207 A

31-416 Cracow

E-mail: wiktorstopyra@gmail.com