Analytic Methods in Assessment of Optic Nerve Cupping

Overview

The intent of this paper is to provide a systems-based analysis of the methods used to evaluate optic nerve cupping, identify potential flaws in these systems, and propose alternatives better to assess this anatomic quantity. Estimation of optic nerve cupping requires an analytic understanding of both the psychophysical as well as the mathematical bases inherent in this measure. When the (decimal-based) cup-to-disc ratio is used to quantitate optic nerve cupping, a one-dimensional, linear estimate is produced, which in turn is derived from two- or three-dimensional, non-linear physical quantities of area or volume, respectively. When extrapolating from volume, to area, to linear measures, due to the psychophysical constraints which limit this task, such a data-compressed estimate of optic nerve cupping may neither accurately reflect, nor correctly represent, the true amount of cupping actually present in the optic nerve head. This type of one-dimensional metric (when comparing calculations from two- or three-dimensional measures over a range of optic nerve cupping), appears to introduce errors which, while most pronounced earlier on in the disease progression, often overestimate the amount of relative cupping (percent cupping) present in a pathological process like glaucoma. The same systemic errors can also lead to overestimation of the progression in cupping, especially in optic nerves with low cup-to disc values. To provide clinically meaningful estimates of optic nerve cupping, the practitioner needs to be aware of psychophysical and mathematical limitations inherent in using a linear cup-to-disc ratio to estimate the amount of cupping observed in a physical structure like the optic disc. The resultant flaws introduced by observer extrapolation from three, to two, to one dimensions (volume, area, and linear); transposition from non-linear to linear quantities; and optical illusions, caused by factors like disc topology, morphology, and ametropia, can all influence subjective-based estimates of optic nerve cupping. To improve clinical outcomes, a non-linear mathematical technique is proposed which utilizes two- or three-dimensional objective measures of optic nerve cupping to describe, more accurately and more precisely, the anatomic quantities (disc, cup, and rim) under discussion. The authors acknowledge that any proposed technique is only a beginning to the work required to improve the clinical value of this type of measure.

Key words:
Optic disc, volume, area, linear measures, optical illusions

Introduction

The intent of this article is to provide a systems-based analysis of the methods used to evaluate optic nerve cupping, identify potential flaws in these systems, and propose alternatives to better assess the anatomic quantities being observed and measured (disc, cup, and rim). Estimation of optic nerve cupping requires an analytic understanding of both the mathematical as well as the psychophysical bases which comprise this measure. From a mathematical basis, attempting to quantitate optic nerve cupping using the traditional, decimal-based, linear cup-to-disc ratio appears to be inherently flawed due to systemic errors which may be present in observation, estimation, and quantitation. These errors may themselves result from an incomplete understanding of the mathematical principles which can influence this observation and the fundamental limitations which can constrain this type of resulting measure.

From a psychophysical basis, errors can be introduced through the very act of observation; from extrapolating from volume, to area, to linear estimations of optic nerve cupping; from illusions induced by the topography and morphology of the optic nerve head; and from magnification and minification effects of ametropia, all of which can affect the observation process. In this paper, we shall assume that the traditional estimate of cup-to disc ratio is linear; while this is often the case and can serve as a useful starting point, in practice there is neither a universal nor a consensus agreement on this type of estimate. Many ophthalmologists can and indeed may use a subjective mixture of one-, two-, or even three- dimensional estimates to attempt to quantitate optic nerve cupping[4].

Background

In using a linear, cup-to-disc system to quantitate optic nerve cupping in a disease like glaucoma, the ophthalmologist attempts to estimate the amount of optic nerve cupping observed during a clinical exam. To use this linear, cup-to-disc measure, the clinician endeavors to apply a one-dimensional, linear system of estimation to approximate quantitation of two- or three-dimensional, non-linear quantities like area and volume, respectively. It is important to note, that in patients with glaucoma, this method of estimation of optic nerve injury, resulting in the linear cup-to-disc measure, may neither accurately reflect nor correctly represent the true amount of relative damage to both the optic nerve head (disc), optic cup, or the neuroretinal rim. Such a one-dimensional metric, when comparing calculations from two- or three-dimensional measures over a range of cupping, appears frequently to overestimate the amount of relative cupping (percent cupping) present in a disease process like glaucoma. It is important to note the relative disparity between linear, area, and volume measures is most pronounced earlier in the glaucomatous process, when less optic nerve cupping is present. While still present throughout the entire range of cupping, this relative disparity appears to be less pronounced later in the glaucomatous process when more optic nerve cupping is indeed present. From a functional point of view (as opposed to the anatomic one discussed herein), where we utilize a subjective response to an objective stimulus, the patient’s response may not be based on the quantity of the cup which is present or absent, but instead may be dependent upon the quantity (as well as quality) of the neuroretinal rim tissue remaining. While not the subject of this paper, the relationships between stimulus and response and between form and function are mentioned to illustrate the complexity of this issue.

In practice, when using the traditional decimal-based cup-to-disc measure to estimate optic nerve cupping, the observer may be unaware of systemic flaws inherent in this method. Let us review some steps in the process. Initially, an observation is made of the optic nerve (cup, rim, and disc) using as a data source, the non-linear physical quantities of area (two-dimensional) and/or volume (three-dimensional) of the patient’s optic nerve head. Next, a transposition is required of and by the observer, to convert the observations made of non linear, two- or three-dimensional physical objects, to a linear, one-dimensional approximation, in an effort to produce the traditional decimal-based cup-to-disc ratio as an estimate of optic nerve cupping. It is through this process of non-linear observation, transposition, and linear approximation, that this method seeks to estimate and quantitate optic nerve cupping in a meaningful way.

We must consider that the ability of most observers, intuitively or accurately, to make such conversions (from three, to two, to one dimensions) may indeed prove to be a challenging and, at times, daunting psychophysical task. Shown experimentally to vary according to Stevens’ Law[6], estimation of a quantity like area or volume is not governed by a linear function - a relation which can be described as R = kS, where R represents the response, S the stimulus, and k a constant, but is instead governed by a power function - a relation which can be described as R = kS^x, where R represents the response, S the stimulus, k a constant, and x the exponent of the power function. This landmark work, detailing the non-linear nature of how the visual system interprets stimuli, is beyond the scope of this paper and is mentioned here for the sake of completeness.

We must note that the use of quantities like area and volume, while probably more accurate and representative as measures of structural damage to the optic nerve, still have inherent limitations in relating the degree of cupping observed by the clinician to the reduction of visual function experienced by the patient, especially when eccentricity of the rim is considered. For simplicity of understanding in the coming examples, comparisons will be confined to those in which the discs and cups are both regular and concentric. While this paper seeks to examine methods to increase the accuracy of quantitating optic nerve cupping, we note these are only a start to the development which will be required in this subject. To conclude, the authors are reminded of the similarity between present methods of optic nerve evaluations and Winston Churchill’s assessment of democratic government: While both may be far from ideal, they are better than anything else we have at this time.

Technique: The Mathematics

First, we shall examine the relationship between disc diameter and disc area as well as that between disc diameter and disc volume. For comparison purposes in the following mathematical discussions, while diameter is a quantity which can be directly measured by the observer, we shall use radius - which is also a linear measure, equal to one half diameter (r = ½d) – to compare the relationships among the different quantities (please note, for ease of comparison, diameter will be used in graphical figures).

Area is related to radius in a non-linear fashion, by a square function. Thus, area is proportional not to radius but to radius raised to the second power (Equation 1).

Equation 1: ∏ A = ∏ r² = ∏ d²/4

For example, with a two fold increase in cup radius, cup area is increased four times; with a three fold increase in cup radius, cup area is increased nine times (see Figure 1). The graphs in Figures 1 and 2 represent the discrepancy between linear, area, and volume calculations for the size of the optic cup, over a range of linear measures of cup radius. Note that the data beneath Figure 1 was used to plot the graphs; Figure 2, represents the discrepancy between linear, area, and volume calculations for the neuroretinal rim (expressed as rim-to disc ratios), over a range of linear cup-to disc values. The discrepancy shown between the linear and non linear measurements will serve as the basis for our argument, of changing the method of measuring the severity of a disease such as glaucoma and of monitoring the progression of this disease.

Volume is related to radius in a non-linear fashion, by a cube function. Thus, volume is proportional not to radius but to radius raised to the third power (Equation 2).

Equation 2: V = 4/3 ∏ r³ = ∏ d³/6

For example, with a two fold increase in cup radius, cup volume is increased eight times; with a three fold increase in cup radius, cup volume is increased twenty-seven times (see Figures 1 and 2).

Next, we shall use this background to examine different optic nerves with different cup-to-disc ratios. We should first point out that in these models, for mathematical purposes, we shall make certain assumptions. We shall assume the cup to be circular in two dimensions and spheroid in three dimensions, with width and length thus equal. We know clinically, this is often not the case. In a disease like glaucoma, the observed cupping can be irregular and / or eccentric in contour and there is often an asymmetry between the horizontal width and vertical length of the cup, yielding a cup that is elliptical and ellipsoid, usually with its major axis in the vertical dimension.

It is important to note, for an ellipse, area is again proportional to the second power of the radius (Equation 3).

Equation 3: A = ∏ (ab), (in which a and b are the radii of the major and minor axes, respectively).

For an ellipsoid, volume is generated by rotating the ellipse about its minor axis (b) and is again proportional to the third power of the radius (Equation 4).

Equation 4: V = 4/3 ∏ (a²)(b), (where a and b are the radii of the major and minor axes, respectively).

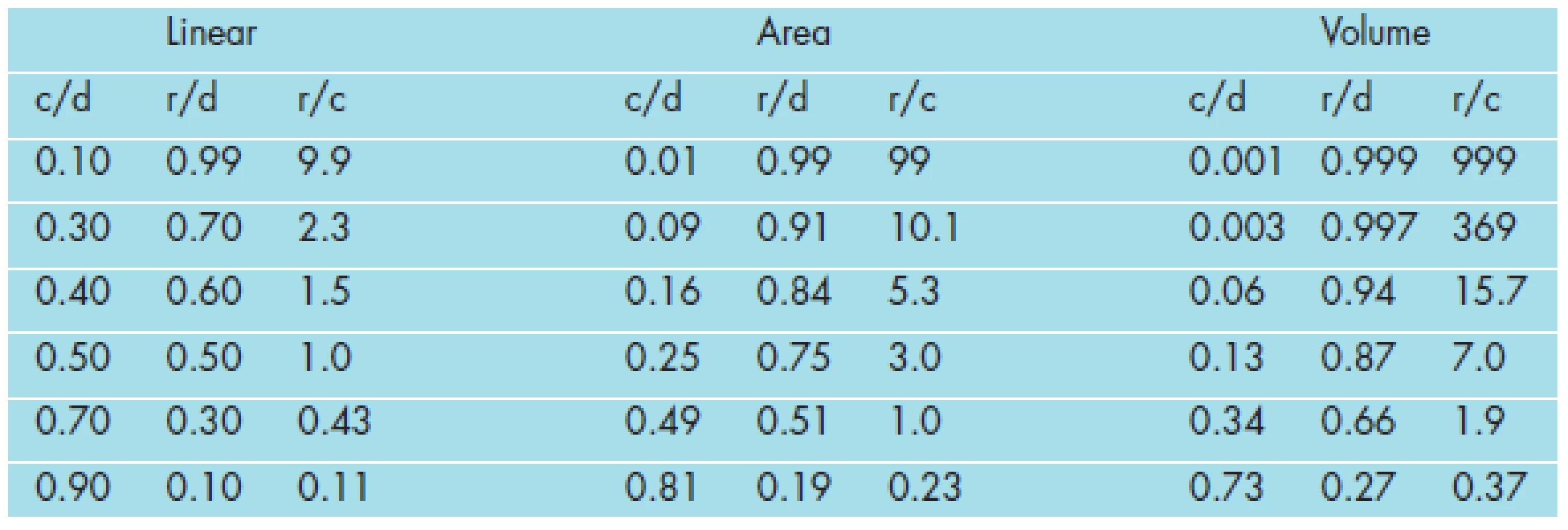
The fact that the optic disc and cup are in practice neither regular nor perfectly round and spherical, does not invalidate the conclusions drawn from the mathematical approximations which follow. While the numbers following do derive from idealized examples of a round as well as spherical cup and disc, the relationships presented, and the comparisons resultant, are nonetheless mathematically valid. As such, these data can and do provide useful tools for clinically meaningful comparisons of the elliptical and ellipsoid cups and discs which clinicians encounter on a regular basis. [N.B.: The optic disc and cup are in reality truncated spheroids. The equation for the surface area of a sphere is ∏d² (or 4 ∏r²) and that for its volume is 1/6 ∏d³ (or 4/3 ∏r³). While these calculations must be divided in half if one uses a truncated half sphere, for comparison purposes, it does not affect the relationships presented herein.] In the calculations which follow we shall assume a circular and spherical cup and disc (see Table 1).

A Cup-to-Disc of 0.5:

In our first example, we examine an optic nerve with a linear cup-to-disc ratio of 0.5 (see Table 1 and Figure 2). This, for example, means in the linear dimension, the cup width or length is estimated to be five-tenths (0.5) that of the disc’s. This leaves an estimation of neuroretinal rim in the linear dimension, of five-tenths (0.5) the width or length of the disc’s, resulting in a rim-to-disc ratio of 0.5 and a rim-to-cup ratio of 1.0, i.e., cup width and rim width are equal, – which suggests that one-half of the disc (50%) has been affected by the disease process.

These relationships, however, will change when the calculation is performed for a circular area in two dimensions. In an optic nerve with a linear cup-to-disc ratio of 0.5, the cup area is 25% and the rim area is 75% that of the disc’s. Thus, the area cup-to-disc ratio is 0.25, area rim-to-disc ratio is 0.75, and area rim-to-cup ratio is 3.0, – which suggests that one-quarter of the disc (25%) has been affected (note the difference compared to the result from the one dimensional linear method above, which yields a value of 50%). While clear in theory and on paper, this mathematical difference is often difficult to observe in a clinical setting.

These relationships change further when the calculation is performed for a spherical volume in three dimensions. In an optic nerve with a linear cup-to-disc ratio of 0.5, the cup volume is 13% and the rim volume is 88% that of the disc’s (note a rounding error). Thus, the volume cup-to-disc ratio is 0.13, volume rim-to-disc ratio is 0.88, and volume rim-to-cup ratio is 7.0, – which suggests that one-eighth of the disc (13%) has been affected (note even a further difference compared to the results from the one-dimensional linear (50%) and two-dimensional area (25%) methods above). For a graphical depiction of the previous discussion, please refer to Figure 2 from which the above three rim values can be estimated.

A Cup-to-Disc of 0.7:

Next, we examine an optic nerve with a linear cup-to-disc ratio of 0.7 (see Table 1 and Firgure 2). This means, in the linear dimension, the cup width or length are each estimated to be seven-tenths (0.7) that of the disc’s. This leaves an estimation of neuroretinal rim in the linear dimension, of three-tenths (0.3) the width or length of the disc’s, resulting in a rim-to-disc ratio of 0.30 and a rim-to-cup ratio of 0.43, – which suggests that seven-tenths of the disc (70%) has been affected by the disease process.

Again, these relationships change when the calculation is performed for an area in two dimensions. In an optic nerve with a linear cup-to-disc ratio of 0.7, the cup area is almost 50% and the rim area is almost 50% that of the disc’s. The area cup-to-disc ratio is 0.49, area rim-to-disc ratio is 0.51, and area rim-to-cup ratio is almost 1.0, – which suggests that almost one-half of the disc (49%) has been affected (note the difference compared to the result from the one dimensional linear method above, which yields a value of 70%).

These relationships also change further when the calculation is performed for a volume in three dimensions. In an optic nerve with a linear cup-to-disc ratio of 0.7, the cup volume is 34% and the rim volume is 66% that of the disc’s. The volume cup-to-disc ratio is 0.34, volume rim-to-disc ratio is 0.66, and volume rim-to-cup ratio is almost 2.0, – which suggests that almost one-third of the disc (34%) has been affected (note even a further difference compared to results from the one-domensional linear (70%) and two dimensional area (49%) methods above). For a graphical depiction of the previous discussion, please refer to Figure 2 from which these values can be estimated.

A Cup-to-Disc of 0.9:

Lastly, we examine an optic nerve with a linear cup-to-disc ratio of 0.9 (see Table 1 and Figure 2). This means, in the linear dimension, the cup width and length are both estimated to be nine-tenths (0.9) that of the disc’s. This leaves an estimation of neuroretinal rim in the linear dimension, of one-tenth (0.1) the width or length of the disc’s, resulting in a rim-to-disc ratio of 0.10 and a rim-to-cup ratio of 0.11, – which suggests that nine-tenths (90%) of the disc has been affected.

Again, these relationships change when the calculation is performed for an area in two dimensions. In an optic nerve with a linear cup-to-disc ratio of 0.9, the cup area is 81% and the rim area is 19% that of the disc’s. The area cup-to-disc ratio is 0.81, area rim-to-disc ratio is 0.19, and area rim-to-cup ratio is 0.23, – which suggests that almost eight-tenths of the disc (81%) has been affected (note the difference compared to the result from the one dimensional linear method above, which yields a value of 90%).

These relationships also change further when the calculation is performed for a sphere in three dimensions. In an optic nerve with a linear cup-to-disc ratio of 0.9, the cup volume is 73%, and the rim volume is 27% that of the disc’s. Thus, the volume cup-to-disc ratio is 0.73, volume rim-to-disc ratio is 0.27, and volume rim-to-cup ratio is 0.37, – which implies almost seven-tenths of the disc (73%) has been affected (note even a further difference compared to results from the one-dimensional linear (90%) and two dimensional area (81%) methods above). For a graphical depiction of the previous discussion, please refer to Figure 2. (Note the percent of affected optic disc and neuroretinal rim tissue using area and volume calculations approach that of the linear calculations at higher values of cup-to-disc ratios.)

In conclusion, when comparing calculations among the three different measures (linear, area, and volume) using the cup-to-disc ratio, the linear method reports more severe loss in structure (more cup and less rim) than the area or the volume methods report, for each of the three different-sized optic cups evaluated (0.5, 0.7, and 0.9 – see Table 1). Likewise, when comparing calculations among the three different measures using the rim-to-disc ratio, the linear method reports more severe loss in structure (less rim and more cup) than the area or the volume methods report for each of the three different-sized optic cups evaluated. For either the cup-to-disc or the rim-to-disc ratios, there is closer agreement among the linear, area, and volume methods at the extreme ends of the range of optic nerve cupping than there is at values in between this range, i.e. for either a very small or very large cup, the three methods of linear, area, and volume calculations converge (see Figure 2). At this point we shall conclude our evaluation and comparison of the mathematics for the different measures (linear, area, or volume) used to estimate optic nerve cupping.

Technique: Induced Optical Illusions

We now turn to examine another potential source of error which can effect observation and estimation of the cup-to disc ratio – induced optical illusions which occur during the assessment of cup, rim, and disc size of the optic nerve. These illusions, of which the observer should be aware, include those induced by: estimation of disc, cup, and rim area, estimation of disc, cup, rim volume, tilt in the optic nerve head, and the magnification / minification effects of ametropia.

Induced Optical Illusions – estimation and physical factors:

In estimating the area of either cup or disc size, optics, mathematics, and observation can initially provide what appear to be confusing results. For example, if one disc is slightly larger than another by a factor of only 1.4 in the linear dimension, the larger disc is in fact twice (2.0 times) as large as the smaller disc, in the area dimension. This type of optical illusion is created by our natural ability, reinforced by repeated behavioral training, to recognize more accurately the linear diameter of a disc than the psychophysical task of a non-linear quantity like its area.

The level of complexity and propensity for induced optical illusion increases when attempting to estimate the volume of either the cup or the disc. If one disc is larger than another, by a factor of 1.6 in the linear dimension, the larger disc is in fact more than quadruple (4.0 times) that of the smaller disc in the volume dimension. This type of optical illusion is further reinforced by behavioral training, in which estimation of a quantity like volume is an unfamiliar, often inaccurate, and sometimes difficult psychophysical task.

Thus, while it has been recognized that deep cups, large cup volumes, and baring of laminar pores can be a sign of advanced glaucoma, shallow-appearing, saucerized cups with end-stage glaucomatous optic neuropathy are also well known to clinicians as an advanced form of optic nerve cupping seen in advanced glaucoma. In such saucerized cups, while their depth is smaller, their width is larger, leading to a significant but sometimes illusively difficult to perceive increase in both cup area and volume. We can use mathematics to de-conflict this type of illusion and to reconcile what is observed with what is clinically apparent. Since volume is a factor of the cube of the radius, while not appearing overly deep, these shallow-appearing but wide cups can still have deceptively large cup volumes, significantly decreased neuroretinal rim volumes, and may indeed manifest severe visual loss on functional testing.

Induced Optical Illusions – Cup variation:

We shall now discuss an optical illusion, which can be induced when observing discs of different sizes (areas / volumes), but which contain the same amount of cupping as provided by the linear cup-to-disc ratio. We consider two discs, both with a reported linear cup-to-disc ratio of 0.6. The first with a disc radius of 0.8 mm (and thus a disc diameter of 1.6 mm), has a disc area of 2.01 sq mm, a cup area of 0.73 sq mm, and a rim area of 1.28 sq mm; has a disc volume of 2.15 cu mm, a cup volume of 0.46 cu mm, and a rim volume of 1.69 cu mm. The second with a disc radius of 0.7 mm (and thus a disc diameter of 1.4 mm), has a disc area of 1.54 sq mm, a cup area of 0.55 sq mm, and thus a rim area of 0.99 sq mm; has a disc volume of 1.44 cu mm, a cup volume of 0.31 cu mm, and a rim volume of 1.13 cu mm (see table 2).

While both discs have an area rim-to-disc ratio of 0.64 and a volume rim-to-disc ratio of 0.79, the larger disc (radius of 0.8 mm) has both a larger cup area (33%) and cup volume (48%) than the smaller disc. Notably the larger disc also has a larger neuroretinal rim area (29%) and neuroretinal rim volume (50%) than the smaller disc. While it is beyond the scope of this paper, such consideration is important to note, because this observation might explain why such a disc, with its larger relative composition of rim tissue, may be more resistant to the neurotoxic effects of glaucomatous optic neuropathy when assessed with functional testing.

The discs and cups of Figure 3 demonstrate the difficulty for an observer visually to discern such differences noted above. Note, the discs below are visual representations of the measurements provided in Table 2 (above); the discs depicted below are magnified fifty times (50x) the actual sizes which are observed clinically (see Figure 3).

Induced Optical Illusions – Disc variation:

An optical illusion can be induced when evaluating a patient with different linear cup-to-disc ratios (cup asymmetry) accompanying different sized optic discs (disc asymmetry). In such an example, a patient can have optic discs of two different sizes, but with (proportionally) different linear cup-to-disc ratios; i.e., a higher cup-to-disc ratio observed in the larger disc and a lower cup-to-disc ratio observed in the smaller disc. What does this mean? Will the smaller cup-to-disc ratio be “cancelled” out by the smaller disc? Not necessarily - as previously noted, the larger disc with “larger” apparent cupping could have more neuroretinal rim area and neuroretinal rim volume than the smaller disc with “smaller” apparent cupping. This difference could have important clinical implications and could explain the asymmetric presentation of glaucoma, often encountered amongst clinicians.

In eyes with similarly-sized optic discs, it is thought that an interocular difference in reported linear cup-to-disc ratio of even 0.1 can be indicative of glaucoma. According to a study performed by Kanski[2], when comparing subjects’ and patients’ eyes with similarly-sized optic discs, in patients’ eyes with an interocular difference in linear cup-to-disc ratios of more than 0.1, 70% of these eyes were reported to have early glaucoma, compared to 8% of (healthy-appearing) subjects’ eyes without such interocular linear cup-to disc disparity. While this finding is interesting, one may wonder if the result cited in Kanski’s fine paper, considered valid within the conventional framework of the linear cup-to-disc ratio, could itself be flawed due to the same systematic errors in technique that the present paper attempts to point out.

Induced Optical Illusions – Tilt:

A different type of induced optical illusion can be caused by tilt of the optic nerve head. When we view and examine the optic disc, we assume the plane of the disc to be perpendicular to the axis of our view. However, physiologic tilting of the optic disc can result in a perceived change to the observer, in the apparent shape of both the disc as well as in the cup. With such tilting, if the horizontal diameter of the disc appears illusively to decrease while the vertical diameter of the disc appears to remain either the same or be increased, the perimeter of the disc may appear to an observer to be more of an oval than a circle (see Figure 4).

For example, in myopic eyes the plane of the disc can be tilted in such a way, that the temporal part of the disc appears behind and the nasal part of the disc appears in front, of the average plane of the disc. This effect of topology could result in an apparent change in both the shape of the disc (from round to oval) and in the shape and depth of the cup (appearing more eccentric and appearing even deeper).

In a similar way, if the cup were to appear steeper on the nasal side and shallower on the temporal side, such an illusion can result in apparent changes to the observed contour of the neuroretinal rim, giving the disc an artifactually saucerized appearance. In discs which are tilted, the apparent position of the central retinal vessels can also appear to shift to a more nasal position than are present in reality, giving the observer the impression that nasalization of the blood vessels has (illusively) occurred. Such induced illusions caused by topology and morphology, should be considered during observation of the optic disc, as they can influence the clinician’s ability to make an accurate diagnosis.

Induced Optical Illusions –Ametropia:

A patient’s own refractive error (ametropia) can also induce an optical illusion to the observer. According to Littmann [3], there is a direct correlation between an observer’s subjective estimation of disc (or cup) area and the amount of refractive error present in the patient’s eye. Due to this illusion, a myopic disc may appear to be smaller in area than it actually is, because a patient’s myopic refractive error can illusively decrease (minify) the apparent size of the optic disc. Likewise, a hyperopic disc may appear to be larger in area than it actually is, because a patient’s hyperopic refractive error can illusively increase (magnify) the apparent size of the optic disc. The relationship between change in observed disc area, compared to real disc area, with patients’ refractive error is: 0.05 sq mm apparent change of disc area per diopter of patients’ ametropia (refractive error). For example, in an emmetrope, a disc with real disc area of 2.0 sq mm would have an apparent observed disc area of 1.7 sq mm if there were 6 diopters of myopia (-6D x 0.05 sq mm/D = -0.3 sq mm; 2.0 sq mm – 0.3 sq mm = 1.7 sq mm) and would have an apparent observed disc area of 2.3 sq mm if there were 6 diopters of hyperopia (+6D x 0.05 sq mm/D = +0.3 sq mm; 2.0 sq mm + 0.3 sq mm = 2.3 sq mm).

Discussion

Several interesting facts emerge from examination of these data, summarized in Tables 3 and 4 below, as cup-to-disc and rim-to-disc calculations for the linear, area, and volume dimensions. For all but the extremes of the range, the amount of cup measured, using the one-dimensional linear cup-to-disc ratio, is more than that measured using the two-dimensional area or the three-dimensional volume calculations (see Figure 2 and please note larger rim value represents a smaller cup size). The corresponding amount of rim measured, using the one-dimensional linear rim-to-disc ratio, is less than that measured using the two-dimensional area or the three-dimensional volume calculations (see Table 4).

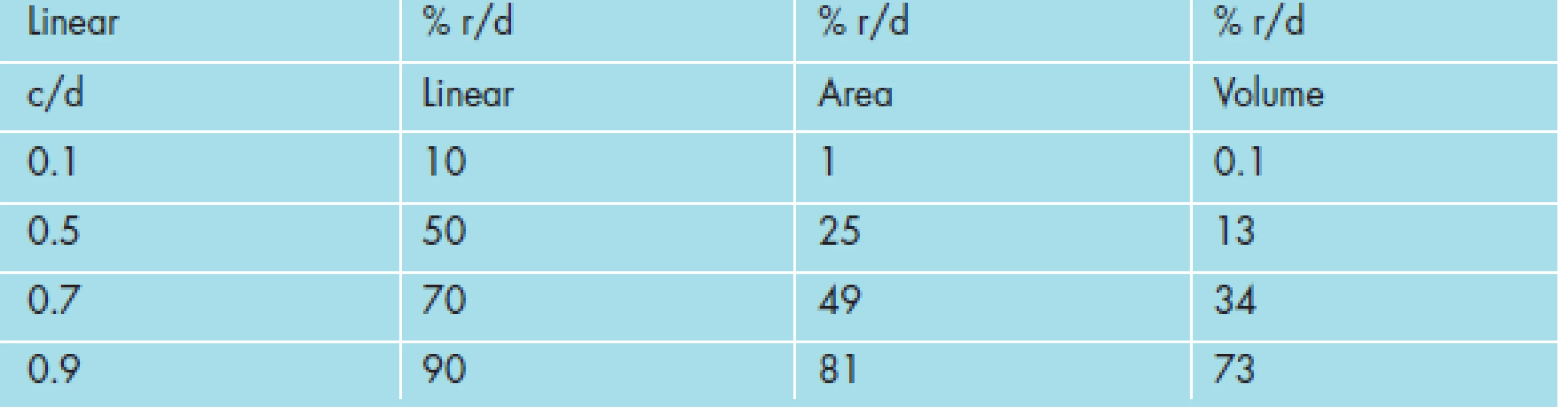
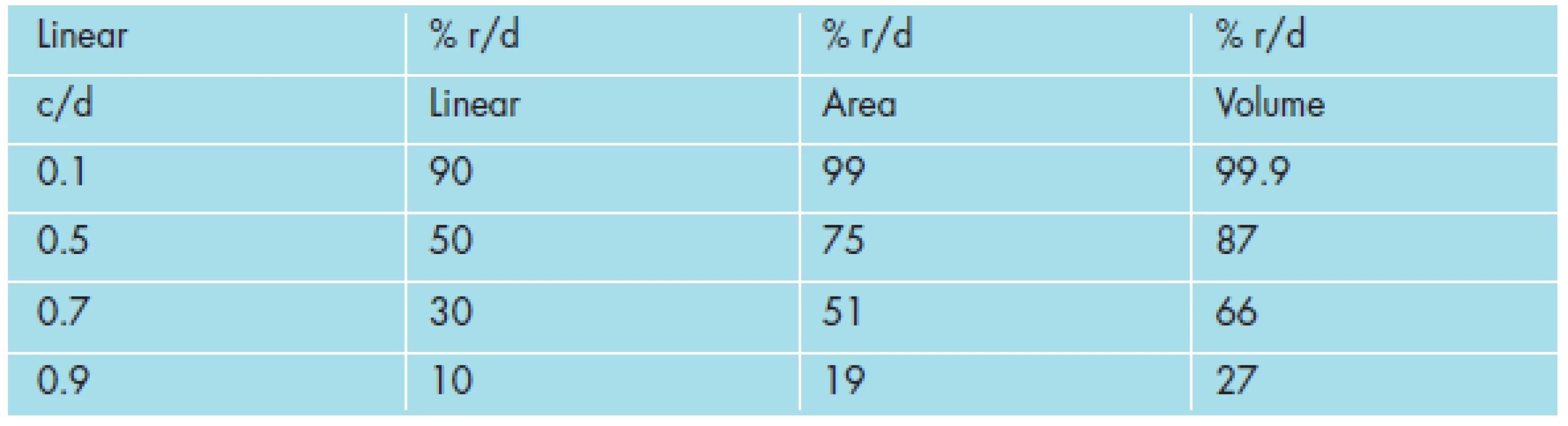
While, the graphs and tables indicate agreement of the three measuring methods (linear, area, volume) at the extremes of cup-to-disc ratio, differences are observed among the three measuring methods at all other points throughout this range. This seems to indicate that the range in which differences in measurements can be viewed most clearly, is also the range of greatest viewing discrepancy. As shown graphically in Figure 2, the maximum difference in measurements centers around the 0.5 linear c/d value.

The points of equality for linear, area, and volume cup and rim values (rim-to-cup ratio = 1.0) occur with progressively larger linear cup-to-disc ratios: approximately 0.5 for linear cup-to-disc ratios, 0.7 for area cup-to-disc ratios, and 0.8 for volume cup-to-disc ratios. Note (for a graphical representation see Figure 2), for all values of linear cup-to-disc ratio (except at the extremes), with the area cup-to-disc ratio and more so with the volume cup-to-disc ratio, the rim appears to comprise a relatively greater proportion of the disc and, correspondingly, the cup appears to comprise a relatively lower proportion of the disc, than would be expected if using the linear cup-to-disc ratio. These differences are represented by the vertical separation in neuroretinal rim values shown in Figure 2.

The differences in these measures and their corresponding rates of change as the cup size increases (which corresponds to the advancement of the glaucomatous disease process) also vary among the linear, area, and volume cup-to-disc ratios. Lower values of linear cup-to-disc ratio (higher values of rim-to-disc ratio) show a lower relative decrease in rate of change in neuroretinal rim area and even less of a relative decrease in rate of change in neuroretinal rim volume, compared to those rates of change seen with progression in cupping at higher values of linear cup-to-disc ratio (or lower values of rim-to-disc ratio). (Referring the reader to basic mathematics, the slopes of the curves in Figure 2 will verify this statement.) The rate of progression of the disease would appear to be directly related to the magnitude of the cup-to disc ratio and as well to the method of its measurement (linear, area, or volume).

To illustrate these points (see Table 5), we shall examine the same change in cupping which occurs from two different baselines. Early in a disease like glaucoma, a change in linear cup-to-disc ratio of 0.4, from 0.1 to 0.5, represents a 44% decrease of neuroretinal rim by linear measure (a change from 0.9 to 0.5), a 24% decrease by area measure, and a 12% decrease by volume measure. Later in the course of the disease, the same change in linear cup-to-disc ratio of 0.4, from 0.5 to 0.9, represents an 80% decrease of neuroretinal rim by linear measure (a change from 0.5 to 0.1), a 75% decrease by area measure, and a 69% decrease by volume measure. Thus, later in the course of the disease, as compared to earlier in the course of the disease, a similar increase in linear cup-to-disc ratio (of 0.4) results in almost two times as much loss of neuroretinal rim by linear measure (80% compared to 44%), over three times as much loss of neuroretinal rim by area measure (75% compared with 24%), and over five times as much loss of neuroretinal rim by volume measure (69% compared with 12%), as the same increase in cup-to-disc ratio (of 0.4) would indicate.

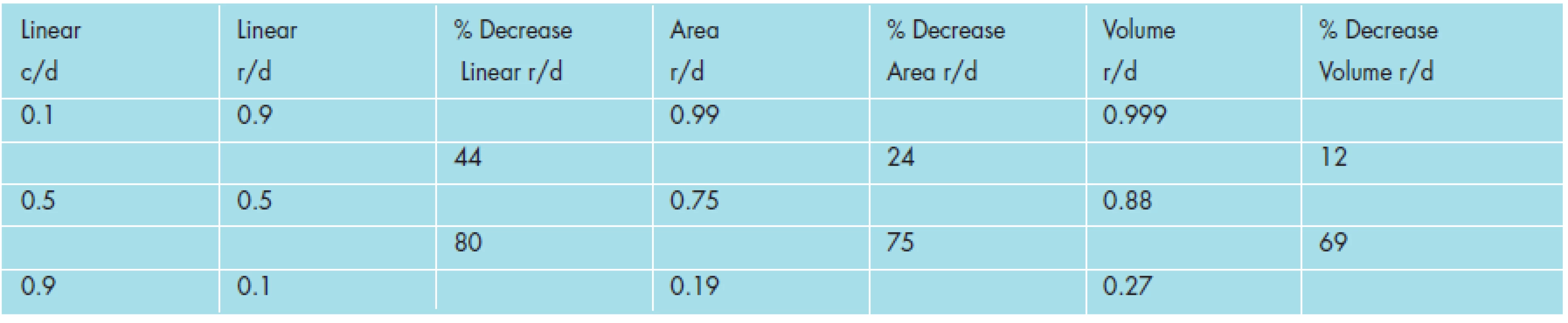
Furthermore, for the same value of change in cupping (of 0.4), occurring earlier in the disease course, the three measures of linear, area, and volume show a relatively wide range of change in the neuroretinal rim, in both absolute and relative terms - from 44% for linear to 12% for volume (a difference of 73%). However, later in the disease course, for the same 0.4 value of change in cupping, the three measures show a relatively narrow range of change in the neuroretinal rim, in absolute and relative terms - from 80% for linear, to 75 % for area, to 69% for volume (a difference of 14%). This represents a five-fold (73% compared to 14%) relative difference in change of the neuroretinal rim between linear and volume measures, when comparing the same value of change in cupping (0.4) at two different baselines of linear cup-to-disc ratio (one at 0.1 and the other at 0.5). It is important to note while using the linear cup-to-disc ratio, when the data are compressed from volume to area to linear measure, this differential effect of change of neuroretinal rim tissue is either not observed or may be lost upon the observer, if conclusions are drawn without appropriate awareness of and correction to the data.

This previous finding is illustrated below in Table 6 (which are comparisons of percent decrease in linear rim-to disc ratio, area rim-to-disc ratio, and volume rim-to-disc ratio compared with changes in linear cup-to-disc (c/d) ratios throughout a range of start and end points). The changes of linear cup-to-disc ratio are grouped sequentially in order of magnitude, in increasing change steps of 0.2 of linear cup-to disc ratios. With increasing quantities of change, the table starts at low linear cup-to-disc values, proceeds to middle linear cup-to-disc values, and finally ends with high cup-to-disc values. Please note all percent values below represent losses (decreases) in rim dimensions and are negative values.

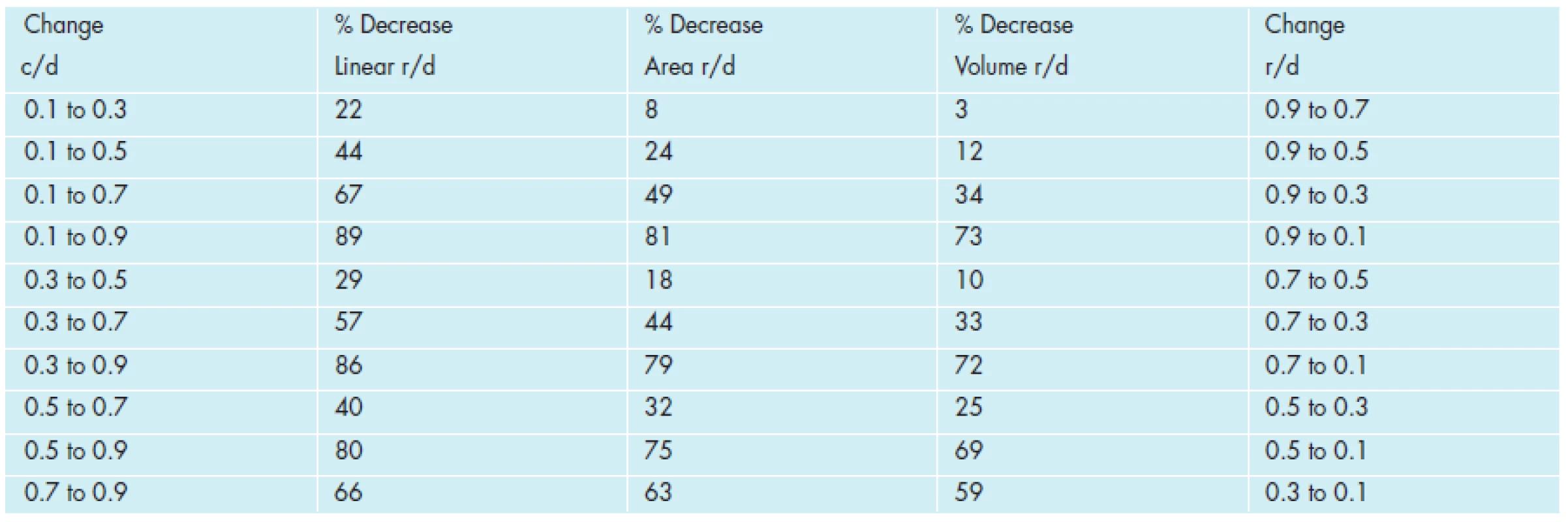
A sample of these findings is also illustrated graphically in Figure 5 below (which represents the rim-to-disc percentage loses in linear (line symbols), area (triangular symbols), and volume (square symbols) with cup to disc changes. The changes for the three dimensions are grouped from 0.1 to 0.3 (three graphs to the left), 0.3 to 0.5 (next graph to the right), 0.5 to 0.7 (third line group to the right) and 0.7 to 0.9 (fourth line group to the right). Note that each group of three plots represent the same difference in linear cup-to-disc change (0.2) but that the three curves are in closer agreement of rim-to-disc loss as the linear cup-to-disc change values become greater.

These observations could explain why in the clinic, so much cupping, in terms of linear cup-to-disc ratio, can be measured early in the course of glaucomatous optic neuropathy with so little apparent evidence of functional impairment (neuroretinal rim tissue by area and more so by volume measure appears relatively spared). This could also explain why so little progression in cupping, in terms of linear cup-to-disc ratio, can so worsen functional measures of optic nerve function later in the course of a disease like glaucoma (neuroretinal rim tissue by area and more so by volume measure appears relatively more affected). A possible explanation for this finding is: in the beginning of the disease there is more neuroretinal rim tissue present than the linear cup-to-disc ratio would indicate, while at the end of the glaucoma process, there is less neuroretinal rim tissue present than the linear cup-to-disc ratio would indicate.

Please note, this neuroretinal rim loss appears to be more accurately represented by area and more so by volume rim-to-disc decreases (see Figure 5), being in closer agreement with subjective observations commonly and traditionally reported by patients on functional testing in the clinic. Thus, at this later level of disease and more advanced level of optic nerve injury, even a small change in cupping results in a (relatively) larger linearly-measured loss of neuroretinal rim tissue with correspondingly greater (and progressive) loss of optic nerve function (the reader is referred again to Figure 5 and Table 6 for elaboration of this point).

We must again note that, in the previous examples, the equations of a circle and a sphere were used to model the area and the volume of the optic disc, rim, and cup. While this is acceptable for simplicity’s sake, we must point out that it is known that the optic nerve head tends to be shaped like a vertical ellipse; that most glaucomatous cupping is irregular in contour (a hallmark of glaucomatous optic neuropathy); and in practice such cupping could be expected to deviate from either an ellipse or an ellipsoid in cross-sectional area or volume measures.

Strictly speaking, an elliptical area or an ellipsoid volume, might appear to be a more approximate measure for the optic cup, disc, and rim that are effected in glaucomatous optic neuropathy. The reader is referred to previous equations for the area of an ellipse [A = ∏(ab)] and the volume of an ellipsoid [V = 4/3 ∏ (a²)(b)]. For ease of calculation and without sacrificing the import of its theoretical significance, in this paper we shall continue to confine our analysis to regular shapes of lines, circles, and spheres.

In considering irregularities to a round and concentric disc and cup, in addition to the elliptical nature of the optic disc, we must also consider the shape and the position of the cup relative to the optic disc. Spaeth and co-workers[5] have shown that a fundamental problem with the use of the linear cup-to-disc ratio in patients with glaucoma is that such a simple ratio does not adequately consider implications for either the shape or the position of the cup, relative to the optic disc. Since eccentric cupping and neuroretinal rim notching are often present in glaucomatous neuropathy, this would appear to be a serious flaw in the linear cup-to-disc estimate. For example, consider a disc with a reported linear cup-to-disc ratio of 0.5. If the disc and cup were concentric, this nerve would have a neuroretinal rim-to disc ratio of 0.25 at both the 6 and 12 o’clock positions (for a total of 0.5). However; if the cup is eccentric, this nerve could have a neuroretinal rim-to-disc ratio of 0.45 at the 12 o’clock position and a rim-to-disc ratio of 0.05 at the 6 o’clock position and still have the same overall rim-to disc ratio of 0.5. (See Figure 6 representing observer’s views of two such discs, noted above, each having a linear cup-to-disc measure of 0.5; the left cup is concentric and the right cup is eccentric.)

While the overall linear cup-to-disc ratios for these two discs are the same, the observer can note the neuroretinal rim areas and rim volumes at specific positions on the two discs appear very different indeed, in spite of their equality of linear cup-to-disc ratios. (Again, the observer tends to be more adept at estimating linear than either area or volume visual measurements). The resultant clinical significance, functional testing, and visual prognosis for each of these discs would be equally different as well.

Given the limitations presented in this paper regarding the linear cup-to-disc system, for estimating and reporting optic nerve cupping, a comment is necessary concerning current alternative methods for estimation and documentation of optic nerve cupping. A requirement in any system would be the ability of the particular system to maintain low intra- and inter-observer variability, as well as, to allow for meaningful and useful comparisons both at different times and/or amongst different observers. The difficult process of evaluating the physical effects of increased cup area and cup volume, compensating for distortions from the ideal norm (in cup contour, topology, morphology, ametropia, and eccentricity), and correctly managing data compression and necessary re-expansion (from three to one dimensions and back again), are currently under study and design.

Rather than attempt to quantitate the entire state of cupping of a particular nerve with one linear cup-to-disc ratio (decimal number), many clinicians are taught to draw the optic nerve head (including the disc, the cup (shape and position), the rim (continuous, sloped, notched, or even absent), and the vessels (nasalized or bayonetted), etc.). Such a method seeks to depict graphically factors like: nasalization, bayoneting, and overpass of vessels, peripapillary atrophy, vertical elongation, focal notching, appearance of lamina dots, and loss of neuroretinal rim. This approach facilitates the observer reaching a conclusion based on the state of the cupping, state of the rim, and the health of the nerve, from the more robust information content contained in this kind of graphical and pictorial data.

High resolution, digitized, stereoscopic disc photographs are often used to supplement optic disc drawings and may be compared over time, to evaluate alteration or progression of optic nerve cupping. Most recently, imaging systems are available and are becoming more common, to utilize digital image analysis and mathematical tools like frequency-domain (spectral) Fourier transforms[1] on techniques like scanning laser polarimetry and optical coherence tomography. This could well be the scope of future papers on this subject, based upon using novel practices to develop a reliable measuring system to overcome the systematic difficulties mentioned throughout this paper.

Such a method, out of design, could eliminate the errors caused by data compression (during observation of the disc) as well as the errors induced by data re-expansion (during estimation of optic nerve cupping), both of which occur when converting between three and one dimensions and back again, when we attempt to produce one decimal-based number for the linear cup-to-disc ratio. Perhaps the best way to explain this phenomenon and our concern regarding the fidelity of this method, is by using the example of digital music systems. The information contained in Beethoven’s majestic 9^th Symphony is such that when properly compressed and re-expanded, the data still accurately represent Beethoven’s 9^th Symphony both in content and to the ear of the listener.

In this process, commonly seen on compact discs (CD’s), the original raw data are still there; they are just compressed for convenience sake and (if done properly) when re-expanded, can be completely and faithfully reproduced in quantity and quality. To even the casual listener’s ear, the two processes must exactly mirror each other. If not, even a piece as sublime to the ear as Beethoven’s 9th Symphony would suffer significant distortions (in data integrity and information content), easily and readily apparent to any listener who heard it. Such is the case with observation and quantitation of optic nerve cupping. When we observe the optic nerve, we compress the data; when we attempt to estimate optic nerve cupping, we re-expand the data. We hope someday to have a system in which, using the musical analogy, after the data compression and re-expansion, not one note is lost, not one note is misplayed, and Beethoven is still, majestically and symphonically, still Beethoven.

Conclusion

Examination and quantitation of optic nerve cupping, using the linear cup-to-disc ratio system, appears to be inherently flawed. Problems with this measure result from errors induced by data compression and re-expansion – i.e., extrapolating from volume (three-dimensional), to area (two-dimensional), to linear (one-dimensional) observations of the optic nerve, disc, rim, and cup, and then back, from linear (one-dimensional), to area (two-dimensional), to volume (three-dimensional) estimations of the size of the optic nerve, disc, rim, and cup. Flaws are noted when using both cup-to-disc (loss of tissue) as well as rim-to-disc (retention of tissue) measures when moving among three, two, and one dimensional estimates. In addition, optical illusions can be induced by estimation of disc, cup, and rim area and volume; by topography, morphology, eccentricity, and tilt of the optic disc, and by magnification and minification effects of ametropia.

Care should thus be taken when using the decimal-based, linear cup-to-disc ratio system in attempting to quantitate and monitor progression of cupping of the optic nerve. Perhaps, when reporting optic nerve cupping caused by a disease process like glaucoma, use of either an area- or volume-based measure, may more accurately and more faithfully describe the information content of quantities like the optic cup, rim, and disc, and may also convey more accurate and more useful information to the clinician. To enhance accuracy and precision, future systems may employ multi-dimensional measurements, using shape-specific formulae which more closely model the actual physical structures under observation along with specific digital compression and re-expansion protocols which will ensure preservation of data integrity. Such a system would more accurately quantitate and report the data both under observation and under consideration.

What the authors propose is a beginning in the incremental nature of trying to advance thought and research in this area – a situation to which the medical field is well accustomed. More work is required, involving devices suitably automated for viewing the optic nerve and measuring, quantitating, and comparing the amount of optic nerve cupping, with appropriate and accurate compensation for errors introduced by data compression and data re-expansion as well as those caused by induced optical illusions, to provide output measures to both the clinician and the patient, that are as accurate and precise, as they are clinically useful and relevant.

Do redakce doručeno dne 7. 1. 2013

Do tisku přijato dne 15. 5. 2014

Lawrence F. Jindra, M.D.

5 Covert Avenue

Floral Park, New York, USA 11001

DrLFJind@optonline.net

(516) 616 - 1710 (O)

(516) 616 - 1700 (F)