Jak lépe pracovat s odbornou literaturou

Overview

Každý urolog bez ohledu na to, zda působí v soukromé praxi nebo na akademické půdě, musí každý měsíc čelit obrovskému přívalu vědeckých statí. Ať se jedná o propagační sponzorované materiály nebo stále se zvětšující objem recenzovaných urologických a chirurgických časopisů, zdá se, že objem literatury, kterou musí urolog zvládnout, je téměř nekonečný. Tento úkol je skličující pro všechny, zejména pro ty lékaře, kteří po ukončení lékařské fakulty neabsolvovali žádný další kurz zaměřený na design klinických studií a biostatistiku. Náš článek se zabývá touto problematikou a uvádí přehled základních principů pro hodnocení literatury na základě statistických modelů. Autor popisuje několik konceptů statistické inference, které mohou být užitečné při kritickém hodnocení literatury.

Klíčová slova:
medicína založená na důkazech, statistika, výsledky, urologie

TESTOVÁNÍ HYPOTÉZY

Testování hypotézy je postup, který kli­ničtí vědci užívají při hodnocení otázek a ověřování nebo vyvracení validity. Jedná se o strukturovaný postup, pomocí něhož lze vyvodit závěr ze souboru údajů (např. srovnání dvou nebo více skupin). Po vytvoření hypotézy je navržena studie, která umožní potvrdit nebo vyvrátit danou hypotézu. Tento koncept je třeba odlišovat od „generování hypotézy“, což je proces shromáždění dat, a na jejich základě vytvoření hypotéz nebo otázek. Povšim­něme si zavedeného pořadí – v případě testování hypotézy je nejprve design studie a poté závěr, zatímco v případě generování hypotézy se nejprve nashro­máždí patřičná data a následně se formuluje otázka. V druhém případě může být závěr vyvozen na základně chybné metodiky vzhledem k tomu, že závěr vy­chází z údajů, které nemusely být nutně nashromážděny pro zodpovězení dané­ho dotazu.

Testování hypotézy vyžaduje nulovou hypotézu (Ho) a alternativní hypotézu (HA). Ho předpokládá, že zastoupení hodnot ve dvou nebo více populacích je totožné – např. objem stolice u kojenců léčených pomocí loperamidu je ekvivalentní jako objem stolice u kojenců ne­užívajících loperamid. HA předpokládá, že zastoupení hodnot ve dvou nebo více populacích není totožné – např. objem stolice u kojenců léčených pomocí loperamidu není ekvivalentní jako objem stolice u kojenců neužívajících loperamid.

CHYBY 1. A 2. DRUHU

Porozumění hypotézám Ho a HA nám pomůže pochopit výskyt dvou základních chyb, k nimž dochází při testování hypotézy – chyb 1. a 2. druhu. K chybě prv­ního druhu (rovněž nazývaná jako α chyba) dochází, pokud nulová hypo­téza platí, ovšem studie tuto skutečnost (tj. že nulová hypotéza je pravdivá) neprokáže. Jinými slovy je možné tvrze­ní, že dvě nebo více skupin mají různá zastoupení, i když ve skutečnosti mají zastoupení stejné. Využijeme opět náš předchozí příklad – předpokládejme, že ve skutečnosti je objem stolice kojenců léčených loperamidem totožný. Výsledek studie však ukazuje, že objem stolice je rozdílný. V tomto případě se jedná o chy­bu prvního druhu (α).

Chyba 1. druhu je hodnota předem sta­novená výzkumníkem během designování studie nebo a priori. Tato chyba by neměla být v žádném případě sta­novena až po analýze souboru dat. Po ukončení studie jsou údaje analyzovány a v případě, že je p-hodnota menší než hladina spolehlivosti α (obvykle, ale nikoliv nezbytně α = 0,05), je tato považována za statisticky signifikantní. Pokud je p-hodnota menší než α hladina, výzkumník potvrzuje statistickou významnost, nebo jinými slovy „zamítne nulovou hypotézu“. Konečně p-hodnotu lze také interpretovat jako pravděpodobnost nesprávného za­mít­nutí nulové hypotézy – tj. pravděpodobnost, že výzkumník potvrzuje existenci rozdílu, ačkoliv ve skutečnosti žádný rozdíl neexistuje.

Podobně chyba 2. druhu (nebo taktéž β chyba) znamená předpoklad tvrzení, že distribuce dvou nebo více populací je stej­ná, ačkoliv se ve skutečnosti liší. K této chybě dochází, pokud alternativní hypo­téza platí, ovšem studie tuto skutečnost neprokáže. Pokud využijeme náš předchozí příklad – předpokládejme, že ve skutečném životě je objem stolice kojenců léčených loperamidem rozdílný, studie však tento fakt neprokáže. V tomto případě se jedná o chybu druhého druhu (β).

Chyba druhého druhu nabývá na vý­zna­mu, pokud se dostáváme ke konceptu „statistické síly“. Sílu studie lze definovat jako schopnost detekovat rozdíly. Mate­maticky se síla vyjádří jako 1-β. Čím nižší je chyba β, tím větší je síla studie. Hodnota β byla na základě úmluvy stanovena na 2,0 (20 %), tato hodnota byla předem domluvena, stejně jako α = 0,05.

Praktickou ukázkou demonstrujeme, jaký klinický význam má změna chyby prvního druhu. Tyto hodnoty jsou opět stanoveny a priori – nikoliv po nashro­máždění dat. Pokud zvolíme nižší α, dojde ke vzniku menšího počtu chyb prvního druhu. Kupříkladu testujeme nový chemo­te­rapeutický protokol pro léčbu povrchového karcinomu močového měchýře o nízkém grade, kdy dosavadní možnosti léčby dosahují vynikajících výsledků. Je třeba se ujistit o tom, že nový medikament je vy­soce účinný – v tomto případě zvolíme níz­kou chybu prvního druhu (např. α = 0,01).

V případě, že zvolíme větší α, dojde k výskytu většího počtu chyb prvního druhu, tj. může se zdát, že je přítomen rozdíl, který ve skutečnosti neexistuje. Kupříkla­du testujeme novou modalitu pro léčbu metastazujícího karcinomu močového měchýře, kdy k dispozici máme pouze velmi málo jiných alternativních možností. V tomto případě se jeví jako logické zvolit větší šanci volbou neúčinné léčby (tj. mů­žeme zvolit α = 0,10) a pokračovat v dal­ším výzkumu.

Užívání chyb prvního a druhého druhu má pro sestavení studie nesmírný význam. Tyto hodnoty jsou stanoveny před zahájením studie a je možné je nastavit na jakoukoli hodnotu klinického scénáře. P-hodnota je naopak stanovena po nashromáždění dat. Jedná se o hodnotu stanovenou na základě výpočtu (podle užívaného statistického nástroje, např. t-test, chí-kvadrát), nikoliv výzkumníkem samotným. Pokud je p-hodnota < než chyba prvního druhu nebo α, je dosaženo statis­tické významnosti.

NEGATIVNÍ STUDIE

Přehled 112 randomizovaných kontrolovaných studií publikovaných v urologic­ké literatuře, které neprokázaly „žádný rozdíl“ mezi léčenými větvemi, prokázal, že dvě třetiny studií nemělo ve skuteč­nosti dostatečnou statistickou sílu [1]. Dvě třetiny studií, které byly v tomto přehledu klasifikovány jako „negativní studie“, by měly být označovány jako „neprůkazné“. K důkazu toho, zda tyto neprůkazné studie jsou skutečně negativní, byly nutné větší studie. Námitka, kterou lze vznést u skutečně negativních studií, je, že nemají dostatečnou statis­tickou sílu – dostatek subjektů, které mohou ospravedlňovat tvrzení, že se jedná skutečně o negativní studii.

Studie bez dostatečné statistické síly představují velké riziko, a to hned z několika důvodů. Zaprvé mohou vést k chybným závěrům, a ohrozit tak další výzkum. Zadruhé mohou být sestaveny způsobem, který vede k plýtvání klinic­kým výzkumem. Dále mohou být subjekty vystaveny zbytečnému riziku, případně se může jevit jako neetické vyvozovat definitivní závěry bez adekvátního výzkumu.

VÝSKYT CHYB PŘI SLOŽITĚJŠÍM TESTOVÁNÍ

Jak již bylo uvedeno, běžná chyba prvního druhu je nastavena na α = 0,05. P-hod­nota < 0,05 je v tomto případě považována za statisticky významnou, což znamená, že existuje 5% pravděpodobnost, že rozdíl vznikl náhodně. Tato statisticky významná p-hodnota = 5 % předpokládá, že je testován pouze jeden nezávislý test. Pokud testujeme více než jeden nezávislý test, je pravděpodobnost, že je signifi­kantní p-hodnoty dosaženo náhodně, vyšší než 5 %. Při provádění dvou nezávislých testů je pravděpodobnost 10 % a při provádění tří nezávislých testů 23 %. V podstatě platí, že čím více testů provádíme, tím vyšší je pravděpodobnost, že náhodně dospějeme k statisticky vý­znamnému výsledku. Přehlédnutí této zvyšující se pravděpodobnosti se nazývá chyba mnohonásobného testování. Jed­nou z celé škály metod umožňujících identifikaci tohoto druhu chyby (a zároveň metodou nejjednodušší) je Bonferroniho test (tab. 1).

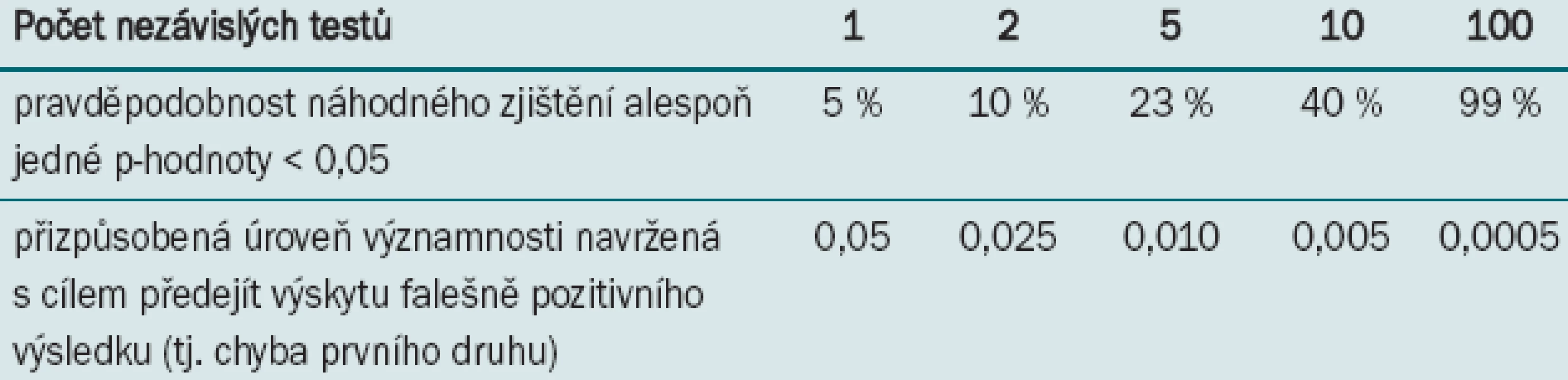
VELIKOST ÚČINKU

Rozdíly (nebo naopak podobnost) růz­ných typů léčby lze nejlépe vyjádřit pomocí veličiny nazývané velikost účinku. Tato veličina může mít celou řadu podob, pečlivý čtenář odborné lite­ratury však porozumí všem. Jednotlivé aspekty lze nejlépe ilustrovat na pří­kladu.

Vezměme si dvě větve randomizované kontrolované studie (RCT) testující skutečnost, zda daný medikament zvy­šu­je mortalitu. Tato studie má dicho­to­mický výsledek (tj. „ano“, pakliže daná skutečnost nastane, a „ne“, pakliže nikoliv). Existuje několik způsobů, jak vyjádřit následující výsledek studie. Ve skupině pacientů užívajících medikament (x) byla zaznamenána 6% míra mortality, zatímco v placeno skupině (y) 10% míra mortality.

Můžeme pouze konstatovat, že apli­ka­ce medikamentu snižuje riziko morta­lity o 4 %, což znamená, že snížení absolutní­ho rizika (ARR) = y – x (0,10 – 0,06 = 0,04).

Další možností jak tento výsledek interpretovat je pomocí relativního rizika (RR), kdy započteme poměr rizika. Každá ze skupin může být čitatel nebo jmenovatel (např. x/y (0,06/0,10 = 0,60), což lze interpretovat jako 60% riziko úmrtí při farmakoterapii (ve srovnání s placebem).

Toto riziko lze dále vyjádřit pomocí snížení relativního rizika (RRR), kdy je ri­zi­ko 1-RR nebo 1 – x/y (1 – 0,60 = 0,40). RRR potom představuje 40% snížení mor­tality při farmakoterapii.

Další metodou je NNT, což vyjadřuje počet pacientů, které je nezbytné léčit za určitý časový interval, aby bylo dosa­ženo pozitivního výsledku nebo zame­zeno výskytu negativní příhody. NNT vypočítáme jako 1/ARR nebo 1/y – x(1/0,04 = 25). Tento výsledek lze interpretovat následujícím způsobem: pro zachránění jednoho života musí léčbu podstoupit 25 pacientů.

Poslední metodou, kterou se bude­me zabývat, je poměr šancí (OR). Pro vysvětlení tohoto konceptu je užitečné po­užít tabulku sestávající ze 2 × 2 buněk (tab. 2). V našem příkladu užijeme údaje ze studie PCPT (tab. 3) [2]. Poměr šancí představuje jednoduše vyhlídky jednotlivých kohort. Nejprve spočítáme na základě údajů PCPT vyhlídky pro každou větev studie zvlášť. Šance vzniku karcinomu prostaty u pacienta užívajícího finasterid je 0,22 = 803/3565, zatímco šance vzniku karcinomu prostaty u pacienta užívajícího placebo je 0,32 = 1147/3545. Oba výsledky následně po­dě­líme a získáváme OR = 0,69 = 0,22/ 0,32. Tuto analýzu lze interpretovat následujícím způsobem: šance, že u pa­cienta užívajícího finasterid dojde v prů­běhu sedmi let (délka trvání PCPT studie) ke vzniku karcinomu prostaty, je 0,69 (ve srovnání s placebem). Nebo jinými slovy: aplikace finasteridu snižuje pravděpodobnost vzniku karcinomu pros­taty o 31 % (1 – 0,69 = 0,31). Povšim­něte si ve schématu 1, že relativní riziko (RR) a poměr šancí (OR) představují matematicky rozdílné výpočty. Existují však případy, kdy se sobě oba výpočty poměrně blíží. V případě, že je riziko [a/(a + b) ] velmi nízké, tzn. hodnota „a“ je velmi nízká, vzorec RR se blíží vzorci OR – tj. a/b. OR a RR se tedy potom stávají ekvivalentní.

Volba prezentace údajů jedním z výše uvedených způsobů závisí pouze na výzkumníkovi. Přesto je důležité, aby čtenář odborné literatury efektu různých metod prezentace údajů rozuměl. Ze­jmé­na velikost účinku je nejzřetelnější při užití RRR (ve srovnání s ARR), jak můžeme vidět v prvním příkladě, kdy je aplikace medikamentu (x) spojena s 6% mírou mortality a aplikace placeba (y) s 10% mírou mortality. Při aplikaci medikamentu bylo zaznamenáno 4% ARR mortality, zatímco RRR mortality bylo 40 %, čímž v druhém případě získá­váme dojem větší účinnosti. Studie spon­zorované komerčními subjekty z tohoto důvodu obvykle upřednostňují uvádění výsledků za pomoci RRR, informovaný a poučený čtenář však bude rozumět efektu jednotlivých způsobů prezentace údajů. Možnost přepočítání výsledků pomocí dalších metod (ARR, OR, RRR, NNT apod.) umožní čtenáři vytvořit si přesnější představu o prezentovaných údajích.

INTERVAL SPOLEHLIVOSTI

Jak přesný byl odhad výsledku léčby?

Odhad výsledku léčby je skutečně pouhý odhad založený na vzorku studie a prav­děpodobně neodráží skutečný odhad vzhledem k tomu, že za daných podmínek nelze testovat celkovou populaci. Výše popsaný výpočet se nazývá bodový odhad. My však potřebujeme vyjádřit odhadované rozmezí skutečného účin­ku. K tomuto účelu se užívá CI (interval spolehlivosti) – měřítko přesnosti. Obvyk­le se uvádí jako 95% CI, což znamená, že s 95% pravděpodobností se náš „pravdivý“ odhad nachází v konkrétním rozmezí hodnot. Tyto složitější výpočty lze provádět pomocí statistických programů, další detaily týkající se této problematiky lze vyhledat v seznamu lite­ratury [3].

PCPT studie uvádí 25% ARR mortality a 95% CI 18–30 %, což jinými slovy znamená, že s 95% pravděpodobností se výzkumníci domnívají, že skutečný odhad poklesu mortality při aplikaci finasteridu leží v rozmezí 18–30 %. V případě, že CI – pro hodnocení velikosti účinku léčby na základě ARR nebo RRR – zahrnuje nulu, hodnoty jsou pova-žo­vá­ny za statisticky nevýznamné (CI v PCPT studii nezahrnoval nulu a vý­sledek byl tedy statisticky významný (p < 0,001)).

ZÁVĚR

Tento článek představuje čtenáři pře­hled základních konceptů statistické inference, která je osnovou pro kritické hodnocení odborné literatury. Pocho­pení této problematiky pomůže čtenáři lépe se orientovat v odborné literatuře a stanovit klinická rozhodnutí.

Roger L. Sur, M.D.
Assistant Professor of Surgery
Division of Urology
UCSD Comprehensive Kidney Stone
Center, Director
200 West Arbor Drive #8897
San Diego, CA 92103
rogersur@mac.com