Resonanční metody měření viskoelasticity biologických struktur

Biologické struktury jsou zpravidla zatěžovány dynamicky a proto statické parametry a charakteristiky k úplnému popisu jejich mechanického chování nepostačují. Deformační odezva při dynamickém zatěžování je totiž ovlivňována energetickými ztrátami. Tyto ztráty souvisejí s tzv. viskózní složkou chování těles. Pokud jsou energetické ztráty nezanedbatelné, mluvíme o viskoelastických tělesech a popis jejich chování musí zahrnovat vliv viscoelasticity. Z matematického hlediska je vztahy mezi namáháními a deformacemi při dynamickém namáhání možné popsat odpovídající diferenciální rovnicí. Praktičtější přístup tradičně vychází z reologických modelů. Moderněji pak z určování komplexních modulů pružnosti, komplexní dynamické tuhosti a mechanické impedance.

Kvantifikace mechanického chování viskoelastických těles vyžaduje v první řadě vhodnou a dostupnou metodiku měření. Pro průmyslové účely jsou pro měření viskoelasticity současné době používány hlavně přístroje typu DMA (dynamic mechanical analysis), založené na měření frekvenčních charakteristik. Pro laboratorní měření na biomedicínských a biomechanických pracovištích jsou určeny RMA (resonance mechanical analysis), pracující na principu mechanické resonance.

Klíčová slova:
Viscoelasticita; měření; komplexní moduly; mechanická impedance;

Úvod

Popis souvislosti mezi deformací a namáháním (dále mechanické chování) je významnou součástí biomechaniky. Vhodná metodika měření je základním předpokladem pokroku v této oblasti.

Důležitá skupina biologických struktur, jako jsou například cévy, kosti nebo fascie, se chová ve fyziologických podmínkách pružně, tedy tak, že po odeznění deformujícího působení se jejich rozměry vrací k původnímu stavu. U lineárně se chovajících těles je relace mezi namáháním a deformací v ustálených stavech plně popsána statickou tuhostí (poměrem mezi silou a deformací). Pokud jsou závislosti nelineární, spočívá řešení problematiky mechanického chování při ustálených stavech v analýze tzv. zatěžovacích diagramů (strain-stress curves). Biologické struktury jsou však zpravidla zatěžovány více či méně dynamicky a pouhé statické charakteristiky k úplnému popisu jejich mechanického chování nepostačují. Deformační odezva při dynamickém zatěžování je totiž ovlivňována energetickými ztrátami. Tyto ztráty souvisejí s tzv. viskózní složkou chování těles. Pokud jsou energetické ztráty nezanedbatelné, mluvíme o viskoelastických tělesech. Naproti tomu často používaná abstrakce, tzv. elastické těleso, disipativní ztráty nebere v úvahu, jinak řečeno elastické těleso nepočítá s vlivem viskózní složky. Použití elastického modelu pro popis chování reálných biologických struktur je tedy principiálně nesprávné a může vést k chybným závěrům.

Znalost mechanického chování viskoelastických těles má potenciálně dalekosáhlý význam. Pro ilustraci uvedeme několik příkladů. Změny viskoelasticity doprovázejí stárnutí organismu, řadu nemocí, průběh regenerace a hojení. Viskoelastické vlastnosti jsou také nezbytné pro stanovení rychlosti deformační odezvy. Tuhost těles při dynamickém zatěžování závisí na viskoelasticitě a liší se od statické tuhosti. Při spojení těles, která mají odlišnou viskoelasticitu, dochází na jejich kontaktu ke vzniku dodatečných namáhání. Viskoelastické parametry přirozených a umělých struktur by proto měly být shodné (struktury by měly být mechanicky přizpůsobené).

Kvantifikace mechanického chování viskoelastických těles vyžaduje v první řadě vhodnou a dostupnou metodiku měření. V současné době se tyto metodiky intenzivně vyvíjejí. Tento přehled pojednává o současných trendech měření viskoelastických charakteristik.

Metody a výsledky

Standardní reologické modely, jejich identifikace a odhad parametrů

Reologické modely [1] jsou založeny na předpokladu, že dynamické chování tělesa lze popsat jako kombinaci pružných elementů (Hookeových těles) a viskózních elementů (Newtonových těles). Velmi často se používá tzv. Voigtův model (obr.1).

Voigtův model

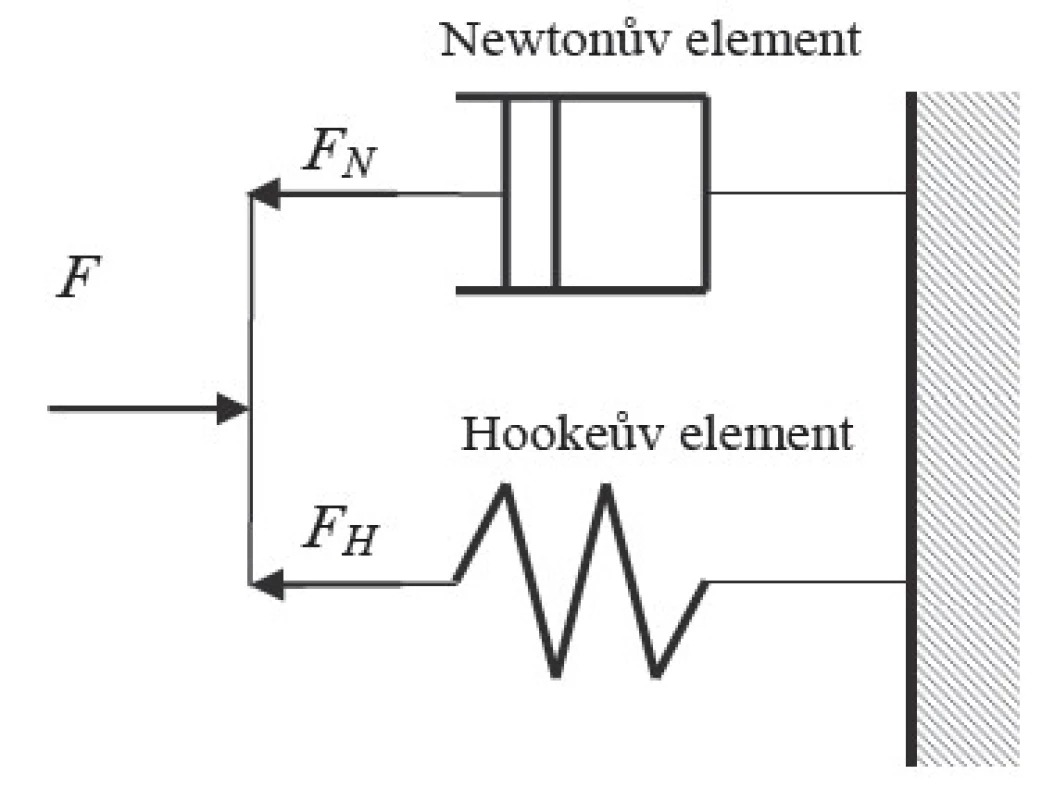
Voigtův model neboli Kelvinovo těleso je tvořen elastickým elementem spojeným s viskózním elementem. Deformace těchto elementů je shodná, celková síla na těleso je rovna součtu sil v dílčích elementech. Platí tedy:

F = F_N + F_H.   (1)

Vztah mezi deformací (L) a silou (F_H) u Hookeova elementu je:

F_H = H.L,   (2)

Hookeův koeficient H odpovídá tuhosti Kelvinova tělesa při statickém namáhání.

Vztah mezi deformací (L) a silou (F_N) u Newtonova elementu je:

Ztrátový výkon P v Kelvinově tělese je:

Newtonův koeficient N tedy vyjadřuje ztráty výkonu v Kelvinově tělese při jednotkové rychlosti deformace.

Pro Kelvinovo těleso jako celek platí vztah:

Pro těleso tvaru tyče o klidové délce L₀ a ploše průřezu S lze vztah (5) přepsat do častěji používané formy:

kde namáhání tyče σ =F/S , modul pružnosti materiálu E = H.L₀/S , viskózní složka materiálu η = N.L₀/S  a relativní deformace ε.

Koeficienty v rovnicích (2 až 6) jsou konstantní v tom smyslu, že nezávisí ani na velikosti deformace ani na rychlosti deformace.

Deformační odezva Kelvinova tělesa na skokovou změnu síly mezi dvěma hladinami (přechodová charakteristika) je dána následujícím vztahem:

kde ΔF je velikost skoku síly.

Vztah (7) lze přepsat do jednodušší formy:

kde ΔL je rozdíl deformací odpovídající rozdílu hladin síly v ustáleném stavu.

Přechodová charakteristika (obr. 2) obsahuje jednu exponenciální závislost. Pokud se těleso chová podle Voigtova modelu, lze na základě měření přechodové charakteristiky odhadnout parametry rovnice (5) i (6).

Složené standardní reologické modely

Pokud složený reologický model obsahuje větší počet dílčích Kelvinových těles zapojených „sériově“, tedy se společnou silou, pak jeho přechodová charakteristika obsahuje více exponenciálních závislostí. Rovnice (8) pak přechází do tvaru (9):

Počet exponenciálních průběhů n v rovnici (9) určuje počet dílčích Kelvinových těles a analýza přechodové charakteristiky umožňuje identifikaci i odhad jejich parametrů.

Meze aplikovatelnosti reologických modelů v biomechanice

Zásadní problém aplikovatelnosti všech standardních reologických modelů spočívá v premise, že chování reálného tělesa odpovídá chování vhodné kombinace konečného počtu pružných a viskózních elementů. Je zřejmé, že tyto modely považují síly spojené s hmotnosti tělesa (setrvačné síly) za zanedbatelné. Tento předpoklad není obecně nikdy zcela splněn. U řady biologických struktur, (např. u měkkých tkání) není splněn ani v reálných podmínkách zatěžování. Již zběžný pohled na teoretický průběh přechodové charakteristiky (vztah 8 a obr. 2) u Kelvinova tělesa napovídá, že zrychlení deformace na počátku přechodové charakteristiky je velmi vysoké. Setrvačné síly jsou přitom podle 2. Newtonova zákona úměrné zrychlení. Podrobnější analýzu těchto a souvisejících problémů nalezne čtenář v monografii [2].

Vliv setrvačných sil se ještě více uplatňuje při praktickém měření viskoelasticity a může zásadně ovlivnit správnost měření. Pokud totiž snímání deformace není prováděno bezkontaktně, je výsledek měření ovlivněn hmotností pohyblivé části měřidla. Zpravidla se jedná o hmotnost svorky a snímače.

Klasické reologické modely je proto třeba rozšířit a reologické modely doplnit o setrvačné elementy. Odhad parametrů je nutno provádět s použitím teorie platící pro takto rozšířené modely.

Mechanická impedance, dynamická tuhost a komplexní moduly

Kvantifikace viskoelasticity nemusí nutně vycházet z identifikace a odhadu parametrů reologických modelů. Modernější metoda vychází z měření mechanické impedance a výpočtu komplexních modulů.

Mechanická impedance Z(iω) (někdy označovaná také jako komplexní mechanická impedance), je poměr fázorů sily F(iω) a rychlosti v(iω) deformace.

Mechanická impedance je komplexní číslo, skládající se z reálné a imaginární části.

Dynamická tuhost G(iω) (někdy označovaná také jako komplexní dynamická tuhost), je poměr fázorů sily F(iω) a deformace l(iω).

Komplexní modul pružnosti E(iω) je poměr fázorů napětí σ(iω) a relativní deformace ε(iω).

Imaginární složka komplexního modulu pružnosti se nazývá loss modulus EL (ztrátový modul) a určuje energii, která se při zatěžování harmonickým mechanickým namáháním o frekvenci ω přemění v teplo.

kde úhel φ je tzv. ztrátový úhel, jedná se o fázový posun mezi harmonickými průběhy napětí a relativní deformace.

Reálná část komplexního modulu pružnosti se nazývá storage modulus E_S (konzervativní modul), který určuje konzervativní energii, která se transformuje mezi elastickou a setrvačnou složku energie bez ztrát.

Platí, analogicky jako u ztrátového modulu:

Na základě vztahů (5) a (10) lze odvodit, že mechanická impedance Kelvinova tělesa je:

Dále, že pro komplexní modul Kelvinova tělesa platí:

Pro ztrátový úhel Kelvinova tělesa platí:

Měření mechanické impedance a komplexních modulů pružnosti

DMA (dynamic mechanical analysis)

Přístroje označované jako DMA se používají pro kvantifikaci mechanických vlastností viskoelastických těles a materiálů [2]. Některé z nich jsou určeny i pro řešení inversního problému u biologických struktur. Měření jsou obvykle založena na určování mechanické impedance a odvozených veličin na základě měření odezev při harmonickém zatěžování. Jedná se tedy o měření frekvenčních charakteristik. Některé varianty však umožňují i měření dalších typů charakteristik (křivky toku, rampové charakteristiky apod.), některé z nich i měření statických charakteristik.

Měření frekvenčních charakteristik v mechanice je technicky náročný problém. Problémy jsou spojeny hlavně s dosažení přijatelné přesnosti a s eliminací chyb vzniklých vlivem setrvačnosti pohyblivé části přístroje. Obtížné je i přesné generování harmonického průběhu sil pro dostatečný interval frekvencí.

RMA (resonance mechanical analysis)

Mechanickou impedanci je možné určovat také na základě frekvence a tlumení vlastních kmitů tělesa. V případě Kelvinova tělesa však vyplývá z teorie, že vlastní kmity nenastávají, protože vlastní kmity jsou spojeny s periodickým „přeléváním“ energie mezi potenciální energii obsaženou v elastickém elementu a kinetickou energii v reálných tělesech obsaženou v hmotnosti tělesa. Z definice Kelvinova tělesa plyne, že setrvačná energie je nulová, protože v modelu chybí setrvačný element. Energie vnesená do Kelvinova tělesa proto nevede ke kmitům, ale k aperiodicky klesající deformaci.

U reálných těles se však s vlastními kmity setkat můžeme, protože se u nich uplatňuje setrvačnost tělesa. Určení mechanické impedance přímo z vlastních kmitů je nicméně málo univerzální metoda. Především proto, že k vlastním kmitům u mnoha těles nedochází v důsledku příliš velkého tlumení.

Tento problém je možno řešit tak, že se jeden konec tělesa zafixuje a na druhý (pohyblivý) konec tělesa se připojí závaží (tzv. setrvačný člen) o známé hmotnosti. Pokud se hmotnost setrvačného tělesa volí dostatečně velká, lze docílit periodické deformační odezvy, tedy vlastních kmitů celé kombinace těleso-setrvačný člen.

Pokud by se například měřené těleso chovalo jako Kelvinovo těleso, je mechanické chování soustavy s připojeným setrvačným členem popsáni rovnicí (18).

Pro průběh vlastních kmitů platí:

kde ω je úhlová rychlost kmitů.

Pokud je hmotnost setrvačného tělesa mnohem větší než hmotnost vzorku, koeficient M přímo odpovídá hmotnosti setrvačného členu.

Pro koeficient a tlumení platí:

Pro frekvenci platí:

Prakticky to znamená, že na základě měření frekvence a tlumení vlastních kmitů lze určit parametry H a N tělesa. Měření je rychlé a není závislé na přesné kalibraci snímače deformace. Výhodou je také to, že vnesení energie je možné provádět pouhým krátkým impulsem síly, jehož velikost neovlivňuje výsledek měření.

Z parametrů H a N tělesa lze dopočítat i modul pružnosti E a viskozitu η, platí:

kde L₀ je klidová délka tělesa a S je plocha průřezu tělesa tvaru tyče.

Analogicky lze postupovat i v případě, že chování tělesa neodpovídá Voigtovu modelu. I když je na obecné úrovni teoretická analýza této situace značně náročná, je ve většině praktických situací možno určovat mechanickou impedanci z vlastních kmitů podle vztahů (25) až (26).

kde je reálná část mechanické impedance a je imaginární část mechanické impedance.

Jinými slovy, na základě tlumení a frekvence vlastních kmitů lze ve většině reálných situací určit mechanickou impedance i odvozené veličiny (komplexní modul a ztrátový úhel).

Poznámka: Vztah (25) platí za předpokladu, že vliv imaginární části impedance na resonanční frekvenci je zanedbatelný. To je obvyklá situace. Ověření platnosti tohoto předpokladu je možné tak, že měříme frekvenci kmitů pro různě velké setrvačné členy. Výpočet reálné části impedance by měl vést ke stejným výsledkům. Pokud tento předpoklad není splněn, je nutno použít poněkud složitější postup.

RMA přístroje pro měření lineárně elastických těles v tahu.

Na resonančním principu byl pro lineárně elastická tělesa na našem pracovišti vyvinut přístroj, jehož schéma je na obr 3. Za lineárně elastická tělesa považujme taková tělesa, jejichž mechanické vlastnosti nezávisí na mechanickém předpětí (klidovém namáhání).

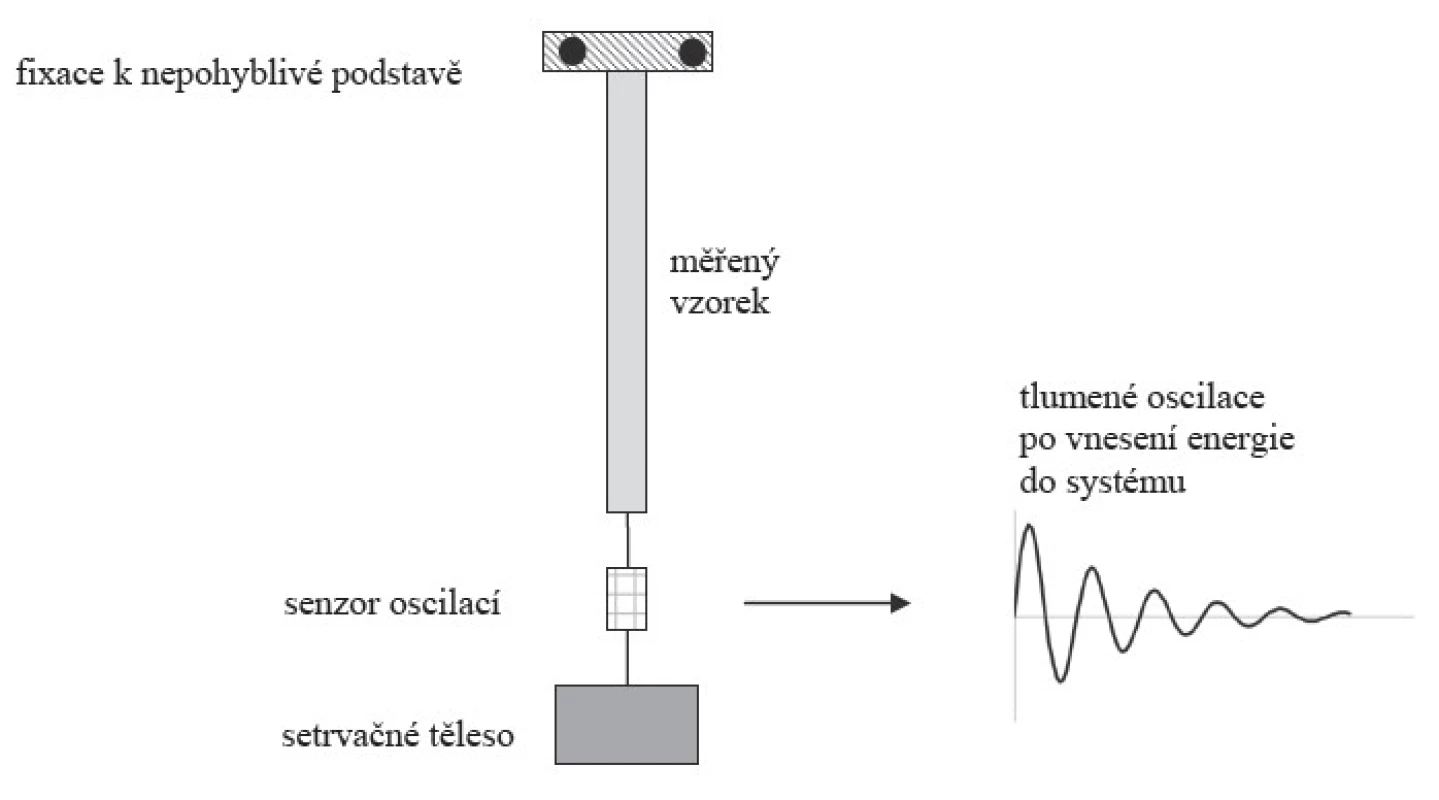
Energie je do systému vnášena elektromechanicky, krátkým poklepem. Deformace je snímána indukčním snímačem, signál ze snímače je elektronicky zpracován, informace je dále vedena do počítače vybaveného softwarem, který na základě vztahů (18 – 26) určuje parametry tělesa. Frekvence kmitů se nastavuje pomocí volby hmotnosti setrvačného tělesa.

RMA přístroje pro měření v tahu nelineárně elastických těles

Řada biologických struktur má parametry závislé na mechanickém předpětí. V měření podle obr. 3 je však předpětí závislé na tíze setrvačného členu a nelze tedy nezávisle nastavit frekvenci a předpětí. Pro měření nelineárně elastických těles byl proto na našem pracovišti vyvinut univerzálnější přístroj, jehož princip je na obr. 4 (kompenzační RMA). Tento přístroj umožňuje nezávisle nastavovat frekvenci kmitů i předpětí. Vliv tíhy setrvačného členu se kompenzuje kalibrovanou pružinou. Vztahy pro výpočet parametrů tělesa (18 – 26) byly doplněny o vliv tuhosti kompenzační pružiny a zahrnuty do používaného software.

Diskuze

Cílem toto pojednání bylo shrnout problematiku týkající se teorie a měření dynamického mechanického chování těles, zejména biologických struktur. Rozsah této problematiky je značný a přesahuje přípustný rozsah této publikace a proto jsou zde uvedeny jen vybrané části teorie, nutné pro porozumění principům měření. Pro hlubší informace odkazujeme čtenáře na naši monografii [2]. Hlavním cílem však bylo shrnout principy činnosti prakticky používané techniky. V současné době jsou pro měření používány hlavně přístroje typu DMA. Ve své většině jsou však tyto přístroje určeny pro průmyslové aplikace. Pro laboratorní měření na biomedicínských a biomechanických pracovištích nejsou obvykle vhodné. Kromě toho, že jsou drahé, jsou málo univerzální a uživatelsky náročné. Diskutabilní je i jejich přesnost. Tato práce proto presentuje i výsledky několikaletého vývoje přístrojů RMA, který probíhá na našem pracovišti [3], [4], [5]. Cílem naší práce byla skupina přístrojů určená pro laboratorní měření. Kromě popsaných přístrojů pro měření v tahu, máme dokončen i vývoj přístrojů pro měření v tlaku a ohybu a speciální přístroj pro měření dynamické tuhosti povrchu těles. Tento přístroj může provádět i měření in vivo, určen je zejména pro měření mechanických vlastností povrchu těla (kůže, jizev apod.).

Závěr

Souprava RMA přístrojů, používaná na našem pracovišti je relativně levná, jednotlivé přístroje jsou řádově levnější než obvyklé aparáty typu DMA. Měření jsou rychlá, dostatečně přesná a uživatelsky nenáročná. Předpokládáme i komerční využití, zejména jako servisní měřicí laboratoř pro biomechanicky a biomedicínsky orientovaná pracoviště.

Poděkování

Autoři děkují za podporu z následujících zdrojů:

Centrum pro přenos technologii UK, Projekt CZ.04.2.06/2.1.00.1/0015.

Grant SVV-2010-261-001.

Kontakt na hlavního autora

Prof. Ing. RNDr. Stanislav Ďoubal, CSc.

Katedra biofyziky a fyzikální chemie, Farmaceutická fakulta University Karlovy, Heyrovského 1203, 500 05 Hradec Králové

Tel: 495 067 483

Fax: 495 067 169

E-mail: doubal@faf.cuni.cz