-
Medical journals
- Career
Noninvasive quantification of alveolar morphometry in elderly never - and ex-smokers
Authors: Gregory A. Paulin 1,2; Alexei Ouriadov 1; Eric Lessard 1,2; Khadija Sheikh 1,2; David G. Mccormack 3; Grace Parraga 1,2
Authors‘ workplace: Imaging Research Laboratories, Robarts Research Institute, The University of Western Ontario, London, Ontario, Canada 2 Department of Medical Biophysics, The University of Western Ontario, London, Ontario, Canada 1; Division of Respirology, Department of Medicine, The University of Western Ontario, London, Ontario, Canada 3
Published in: Physiological Reports, 3, 2015, č. 10, s. 1-13
Category: Original Research
doi: https://doi.org/10.14814/phy2.12583© 2015 The Authors. Physiological Reports published by Wiley Periodicals, Inc. on behalf of the American Physiological Society and The Physiological Society.
This is an open access article under the terms of the Creative Commons Attribution License, which permits use, distribution and reproduction in any medium, provided the original work is properly cited.Overview
Diffusion‐weighted magnetic resonance imaging (MRI) provides a way to generate in vivo lung images with contrast sensitive to the molecular displacement of inhaled gas at subcellular length scales. Here, we aimed to evaluate hyperpolarized 3He MRI estimates of the alveolar dimensions in 38 healthy elderly never‐smokers (73 ± 6 years, 15 males) and 21 elderly ex‐smokers (70 ± 10 years, 14 males) with (n = 8, 77 ± 6 years) and without emphysema (n = 13, 65 ± 10 years). The ex‐smoker and never‐smoker subgroups were significantly different for FEV1/FVC (P = 0.0001) and DLCO (P = 0.009); while ex‐smokers with emphysema reported significantly diminished FEV1/FVC (P = 0.02) and a trend toward lower DLCO (P = 0.05) than ex‐smokers without emphysema. MRI apparent diffusion coefficients (ADC) and CT measurements of emphysema (relative area–CT density histogram, RA950) were significantly different (P = 0.001 andP = 0.007) for never‐smoker and ex‐smoker subgroups. In never‐smokers, the MRI estimate of mean linear intercept (260 ± 27 μm) was significantly elevated as compared to the results previously reported in younger never‐smokers (210 ± 30 μm), and trended smaller than in the age‐matched ex‐smokers (320 ± 72 μm, P = 0.06) evaluated here. Never‐smokers also reported significantly smaller internal (220 ± 24 μm, P = 0.01) acinar radius but greater alveolar sheath thickness (120 ± 4 μm,P <0.0001) than ex‐smokers. Never‐smokers were also significantly different than ex‐smokers without emphysema for alveolar sheath thickness but not ADC, while ex‐smokers with emphysema reported significantly different ADC but not alveolar sheath thickness compared to ex‐smokers without CT evidence of emphysema. Differences in alveolar measurements in never ‐ and ex‐smokers demonstrate the sensitivity of MRI measurements to the different effects of smoking and aging on acinar morphometry.
Keywords:
Acinar duct, emphysema, hyperpolarized 3He magnetic resonance imaging, lung morphometry, senile emphysema.Introduction
Senile emphysema – the normal changes of the lung parenchyma that accompany aging – is characterized by distal airway enlargement without obvious fibrosis or alveolar wall destruction (Verbeken et al. 1992). Other structural components include the loss of elastic fibers, thickening of alveolar walls (Verbeken et al. 1992), and diminished pulmonary elastic recoil (Frank et al. 1957; Thurlbeck 1967; Turner et al. 1968). In concert with the pathological changes that accompany aging, increased residual volume (RV), functional residual capacity (FRC) (Janssens et al. 1999), and decreased diffusing capacity of carbon monoxide (DLCO) (Janssens et al. 1999), forced expiratory volume in 1 sec (FEV1), and forced vital capacity (FVC) (Fletcher and Peto 1977) are also observed.
Senile emphysema in elderly never‐smokers is not commonly accompanied by clinical symptoms or pulmonary function measurements typical of smoking‐related emphysema (Laennec and Forbes1834). Emphysema that commonly accompanies chronic obstructive pulmonary disease (COPD) may be differentiated from the lung changes associated with aging by the deformation of alveoli as a result of fibrosis and tissue destruction, resulting in reduced surface area for gas exchange (Hogg2004). Importantly, older adults typically report lung function that deteriorates with age, but in the elderly, such normal (age‐normalized) lung function is sufficient for routine day‐to‐day activities (Mayer et al. 1958). However, there is an increased risk of breathlessness and respiratory failure in the elderly, and these may further complicate other comorbidities of aging (Peterson et al. 1981; Young et al. 1987; Sharma and Goodwin 2006). In addition, age‐dependent lung structural and functional differences can reduce the sensitivity of the respiratory centers in the presence of hypoxia or hypercapnia, resulting in a diminished ventilatory response in cases of heart failure or aggravated airway obstruction (Kronenberg and Drage 1973; Peterson et al. 1981; Janssens et al. 1999).
Hyperpolarized inhaled noble gas magnetic resonance imaging (MRI) provides noninvasive, in vivo measurements of lung function and structure (Yablonskiy et al. 2002; Fain et al. 2005; Evans et al.2007; Parraga et al. 2007; Kirby et al. 2010) showing those regions of the lung that participate in ventilation and those that do not (Parraga et al. 2008; Kirby et al. 2010). In addition, the MRI apparent diffusion coefficient (ADC) for inhaled gases is sensitive to changes in the lung microstructure and airspace size correlating well with age (Fain et al. 2005), spirometry measurements (Salerno et al. 2002), DLCO (Fain et al. 2006), and X‐ray computed tomography (CT) measurements of emphysema (Diaz et al. 2009). Previous studies have also shown the strong agreement for alveolar parameters obtained using 3He MRI and those estimated using histology (Yablonskiy et al. 2009). The relationships between MRI estimates of the mean linear intercept and pulmonary function measurements have also been shown in mild to severe cases of COPD (Woods et al. 2006; Yablonskiy et al. 2009; Quirk et al. 2011).
On the basis of the previous work, we hypothesized that elderly ex ‐ and current smokers would report significantly increased external airway radius (R) and mean linear intercept (Lm), compared to elderly never‐smokers. Therefore, the aim of this work was to use MRI to provide ADC and acinar/alveolar morphometry estimates in elderly never‐smokers and ex‐smokers as a first step toward understanding lung aging in relation to smoking history and other measurements of pulmonary function.
Methods
Study volunteers and design
Participants provided written informed consent to a study protocol approved by the local research ethics board and Health Canada. Never‐smokers aged 60–90 years with ≤0.5 pack–years smoking history and without acute or chronic respiratory disease, as well as smokers aged 60–90 years with >10 pack‐years smoking history and were evaluated using spirometry, plethysmography, hyperpolarized 3He MRI, and CT during a single 2‐h visit.
Pulmonary function measurements
Spirometry was performed to acquire the forced expiratory volume in 1 sec (FEV1), forced vital capacity (FVC), and FEV1/FVC according to American Thoracic Society (ATS) guidelines (MedGraphics Corporation, St. Paul, Minnesota) (Miller et al. 2005). Body plethysmography was performed for the measurement of lung volumes, and DLCO was measured using the gas analyzer (MedGraphics, St. Paul, MN).
Image acquisition
MRI was performed on a whole body 3 T MRI system (MR750 Discovery, GEHC, Milwaukee, WI) with broadband imaging capability. All 3He MRI employed a whole body gradient set with maximum gradient amplitude of 4.8 G/cm and a single‐channel, rigid elliptical transmit/receive chest coil (RAPID Biomedical GmbH, Wuerzburg, Germany). The basis frequency of the coil was 97.3 MHz and excitation power was 2 kW using an AMT 3T90 RF power amplifier (GEHC). Subjects were positioned supine in the scanner and for both 1H and 3He MRI, subjects were instructed by a pulmonary function technologist to inhale of 1.0 L 3He/N2 a gas mixture (20%/80% by volume) from functional residual capacity (FRC), with image acquisition performed under breath‐hold conditions as described previously (Parraga et al. 2007). Diffusion‐weighted 3He MRI data were acquired using a multislice interleaved 2D gradient echo diffusion‐weighted sequence with a matrix size of 128 × 80, for seven 30‐mm coronal slices (900 μsec selective RF pulse, flip angle θ = 4°, TE = 3.9 msec, TR = 5.6 msec, bandwidth = 62.5 kHz, b = 0, 1.6, 3.2, 4.8, 6.4 sec/cm2); the diffusion‐sensitization gradient pulse ramp up/down time was 500 μsec with a diffusion time of 1460 μsec. The potential for image artifacts associated with RF pulse “history” (Miller et al. 2004) was addressed by using an optimal constant flip angle of 4 degrees (Ouriadov et al. 2009). A diffusion‐sensitizing, gradient‐step, k‐space acquisition scheme starting at the maximum b value was used to ensure that maximum MR signal was acquired for diffusion‐weighted images at greaterb values. All five b‐value images were acquired during a single 15 sec breath‐hold.
Thoracic CT was acquired on a 64‐slice Lightspeed VCT scanner (GEHC) (64 × 0.625 mm, 120 kVp, 100 effective mA, tube rotation time of 500 msec, and a pitch of 1.0). A single spiral acquisition of the entire lung was acquired from the apex to the base with subjects in the supine position and in breath‐hold after inhalation of a 1.0 L 4He/N2 mixture from FRC. Images were reconstructed using a slice thickness of 1.25 mm with a standard convolution kernel. The total effective dose for an average adult was 1.8 mSv.
Image analysis
Ventilation defect percent (VDP) measurements were generated by one observer using semiautomated segmentation software as described previously (Kirby et al. 2012). 3He MRI ADC analysis was performed using MATLAB R2013b (MathWorks, Natick, MA). To ensure that ADC values were generated for voxels corresponding to ventilated lung regions, a k‐means clustering algorithm (Kirby et al. 2012) was applied to the nondiffusion‐weighted images (b = 0 s/cm2) to obtain a binary mask for each slice. The resulting binary masks were then applied to the corresponding diffusion‐weighted images (b = 1.6 sec/cm2), and ADC maps were generated on a voxel‐by‐voxel basis as described previously (Yablonskiy et al. 2002).
The minimum signal‐to‐noise ratio (SNR) of 40 (Ouriadov et al. 2014) for the b = 0 sec/cm2 image and the minimum SNR of 5 for the b = 6.4 sec/cm2 image were used as thresholds for the generation of morphometric estimates. For each subject, a single region‐of‐interest (ROI) (approximately 100 voxels) inside the lung was used to obtain the mean signal value for SNR measurements. A single ROI outside of the lung was used to estimate the signal in regions of the image with mainly noise. The standard deviation of the signal value measured outside the lung was used to estimate noise (approximately 100 voxels) and SNR was calculated based on the following equation:
A Hann filter was applied to maximize SNR of images. The SNR threshold of 40 for b = 0 images was used as described previously (Ouriadov et al. 2013) to mitigate potential errors in the anisotropic diffusion coefficient estimations and consequently, errors in the morphometric parameters. The SNR threshold of 5 for b = 6.4 sec/cm2 images was used because this is the minimum threshold acceptable for quantitative image analysis (Rose 1948).
The relative area of the CT density histogram with attenuation values less than −950 Hounsfield units (RA950) was determined using Pulmonary Workstation 2.0 (VIDA Diagnostics Inc., Coralville, IA). The CT density threshold for RA950 greater than 6.8% was used (Gevenois et al. 1996) to classify smokers with and without emphysema.
Lung morphometry calculations and estimates
A schematic for the MRI morphometry data generation is provided in Figure 1. As described previously (Sukstanskii and Yablonskiy 2008), anisotropic diffusion coefficient maps were generated using a custom‐built IDL 6.4 algorithm which fit equation (2) to multiple b‐value measurements of the 3He diffusion‐attenuated MR signal on a voxel‐by‐voxel basis (Ouriadov et al. 2013, 2015) with the assumption of constant DL and DT values. The same ADC binary masks were applied to the corresponding diffusion‐weighted images prior to fitting. Using this approach, S0 is the MR signal intensity in the absence of diffusion‐sensitizing gradients, Φ(z) is the error function
DL is the longitudinal diffusion coefficient, and DT is the transverse diffusion coefficient.
Equations (2), (3), (4) were used to calculate the geometrical expressions for internal (r) and external (R) airway radius, using equations (5), (6), (7), (8), (9), (10) developed previously (Yablonskiy et al. 2002, 2009) on a voxel‐by‐voxel basis using previously published fitting algorithm (Ouriadov et al. 2014, 2015), where R, r, and D0 were the fitting variables. For a physiological range of geometrical parameters r and R (r/R > 0.4) (Yablonskiy et al. 2009), and for gradient strengths typical of clinical scanners, the following equations may be used (Sukstanskii and Yablonskiy 2008):
which account for non‐Gaussian diffusion in acinar airways, where βL and βT are the coefficients that reflect non‐Gaussian diffusion effects (Sukstanskii and Yablonskiy 2008), DL0 and DT0 are anisotropic diffusion coefficients at b = 0 sec/cm2, where L1 and L2 are the characteristic diffusion lengths for one ‐ and two‐dimensional diffusion
and
and D0 is the unrestricted diffusion coefficient for 3He in the gas mixture. Previous simulations showed that 1.6–1.8 msec is the optimal diffusion time to permit alveolar measurements in mild and moderate COPD (Yablonskiy et al. 2009). Two conditions also determine the maximum b value (Yablonskiy et al.2009) such that DL and DT can be estimated if: (1) bmax (DL - DT) >1; and (2) bmax DT > 1, that is, a maximum b value should be greater than 6 sec/cm2. Finally, parameters such as alveolar depth (h), alveolar length (L), surface area‐to‐volume ratio (S/V), and mean linear intercept (Lm) were calculated on a voxel‐by‐voxel basis by fitting morphometry map data into equations (11) through(13) (Yablonskiy et al. 2009).
Figure 1. Schematic for pipeline required to derive morphological parameters from <sup>3</sup>He diffusion‐weighted MRI. Anisotropic diffusion coefficient maps were generated using a custom‐built IDL 6.4 algorithm which fit equations (2), (3), (4) to multiple b‐value measurements of the <sup>3</sup>He diffusion‐attenuated MR signal on a voxel‐by‐voxel basis. Anisotropic diffusion coefficients were substituted using phenomenological expressions (5), (6), (7), (8), (9), (10) in order to generate morphometry maps: internal (r) and external (R) airway radius. Alveolar depth (h), alveolar length (L), surface area‐to‐volume ratio (S/V), and mean linear intercept (L<sub>m</sub>) were calculated on a voxel‐by‐voxel basis using morphometry map data in equations (11), (12), (13). 
Statistical analysis
Independent t‐tests, tests for normality (determined with a Shapiro–Wilk test), and analysis of variance with post hoc analysis using the Holm–Bonferroni correction were performed using SPSS Statistics, V22.0 (SPSS Inc., Chicago, IL). For measurements that were not normally distributed, multiple comparisons were evaluated using the Kruskal–Wallis test with Dunn's correction. The relationships between morphometry and spirometry measurements were evaluated using Pearson correlations performed using GraphPad Prism 4.01 (GraphPad Software, La Jolla, CA; 2004). Results were considered statistically significant when the probability of making a Type I error was less than 5% (P < 0.05).
Results
Demographics and pulmonary function measurements
As shown in Table 1, 59 participants were enrolled including 38 never‐smokers (73 ± 6 years, 15 males) and 21 ex‐smokers (70 ± 10 years, 14 males) all of whom provided written informed consent to an ethics board approved protocol. Table S1 (online only) provides a by‐subject list of all demographic data that are summarized in Table 1. There were significant differences observed between never ‐ and ex‐smokers for FEV1 (P = 0.02), FEV1/FVC (P = 0.0001), RV/TLC (P = 0.01), and DLCO (P = 0.002) but not for age, BMI, FVC, or TLC. Ex‐smokers were classified based on the presence or absence of emphysema measured using the CT RA950 threshold described previously (Gevenois et al. 1996) and there was no significant difference in smoking history between the two subgroups (ex‐smokers = 40 ± 21 pack‐years, ex‐smokers with emphysema = 44 ± 31 pack‐years, ex‐smokers without emphysema = 38 ± 12 pack‐years; unadjusted P = 0.62). The average years since smoking ceased for all ex‐smokers was 17 ± 12 years (ex‐smokers with emphysema = 20 ± 14 years and ex‐smokers without emphysema = 15 ± 12 years; unadjustedP = 0.47). Ex‐smokers with emphysema reported a trend toward diminished FEV1/FVC (P = 0.05) and a trend toward abnormal DLCO (P = 0.05) compared to ex‐smokers without emphysema. As shown in Table S1, two never‐smokers reported FEV1/FVC <0.70 and four ex‐smokers without emphysema also reported FEV1/FVC <0.70 and FEV1 consistent with GOLD grade I (n = 2) or grade II (n = 2) COPD.
1. Participant demographics 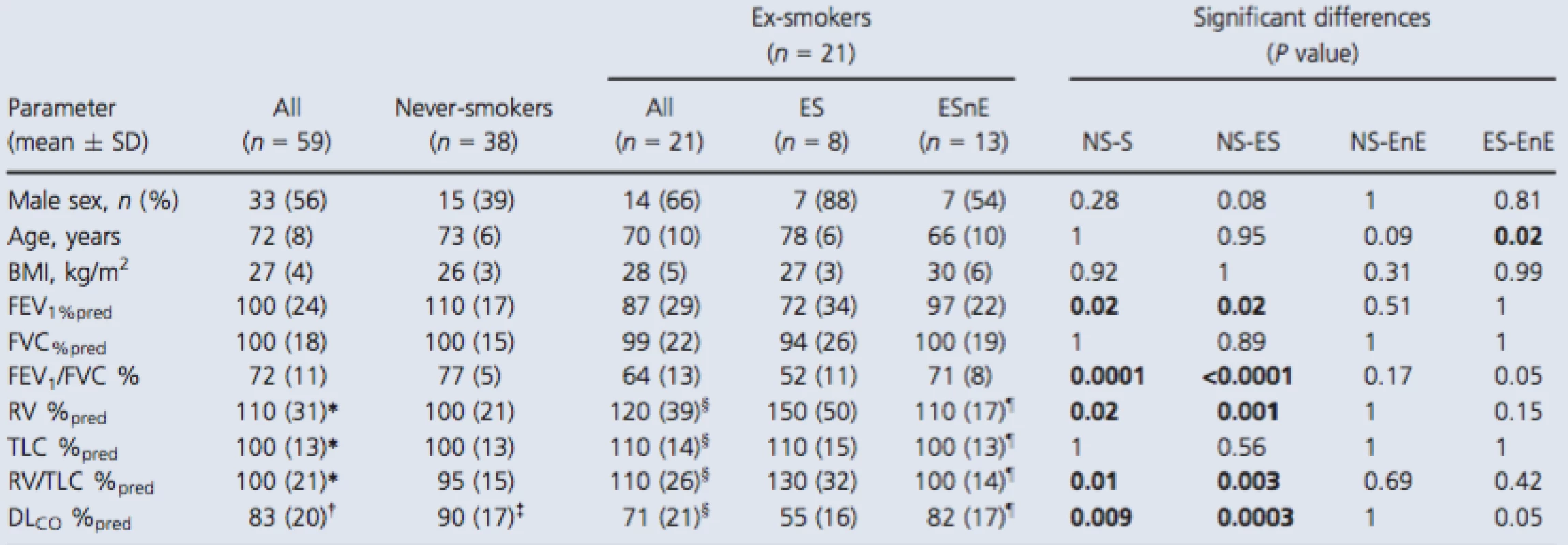
Significant differences (P value) generated using a Kruskal–Wallis test with Dunn's correction. Bold values denotes significant difference (P < 0.05). SD, standard deviation; BMI, body mass index; FEV1, forced expiratory volume in 1 sec; %pred, percent predicted; FVC, forced vital capacity; RV, residual volume; TLC, total lung capacity; DLCO, diffusing capacity of the lung for carbon monoxide. *n = 58, †n = 55, ‡n = 36, §n = 20, ¶n = 12. Imaging measurements
Figure 2 shows the center coronal 3He ventilation, ADC, and internal (r) and external (R) acinar duct radii maps for two representative never‐smokers and two ex‐smokers. The same binary masks were applied for calculation of ADC and morphometry maps. The morphometry approach is complex and fitting does not always converge for all pixels and this, in some circumstances leads to voids in the morphometry maps. For the two never‐smokers there was homogeneous ventilation and the ADC and morphometry maps were also regionally homogeneous with very similar mean values across the entire lung. The global mean value of the free diffusion coefficient D0 was 0.84 cm2/sec. For the two older ex‐smokers, and especially Subject SE‐02, there was visual evidence of patchy ventilation with ventilation defects obvious in the peripheral lung, as described previously (Mathew et al. 2008).
Figure 2. <sup>3</sup>He center slice static ventilation, ADC, and morphometry maps. Hyperpolarized <sup>3</sup>He static ventilation, ADC, and morphometry maps for two representative older never‐smokers and two ex‐smokers. ADC, apparent diffusion coefficient; r, internal airway radius; R, external airway radius. NS‐01: female, 77 years old; FEV1%<sub>pred</sub> = 91; VDP = 1.5%; ADC = 0.24 cm<sup>2</sup>/sec; RA<sub>950</sub> = 0.75%. NS‐15: female, 69 years old; FEV1%<sub>pred</sub> = 91; VDP = 2.4%; ADC = 0.20 cm<sup>2</sup>/sec; RA<sub>950</sub> = 0.44%. EnE‐03: male, 62 years old; FEV1%<sub>pred</sub> = 70; VDP = 9.1%; ADC = 0.29 cm<sup>2</sup>/sec; RA<sub>950</sub> = 4.0%. E‐02: male, 79 years old; FEV1%<sub>pred</sub> = 126; VDP = 16%; ADC = 0.42 cm<sup>2</sup>/sec; RA<sub>950</sub> = 11%. 
Table 2 shows MRI measurements of tissue integrity (ADC) and MRI alveolar morphometry estimates as well as RA950, a well‐understood CT measurement of emphysema for all subjects, and the never ‐ and ex‐smoker subgroups. Table S2 (online supplement) provides a subject listing of these data. As shown in Table 2, 3He ventilation defect percent (VDP), diffusion (ADC, and DT) and two morphometry estimates (r, h), as well as CT‐derived RA950 were significantly different between never‐smokers and smokers. The mean DL and DT estimates for never‐smokers and smokers indicated that conditions bmax (DL − DT) > 1 and bmax DT > 1 were satisfied for the maximum b value (6.4 sec/cm2) used. In addition, as compared to literature reported values for young never‐smokers, the elderly never‐smokers investigated here reported greater ADC values (Fain et al. 2005; Altes et al. 2006), acinar duct radius, and mean linear intercept (Quirk et al. 2015).
2. 3He MRI and CT measurements 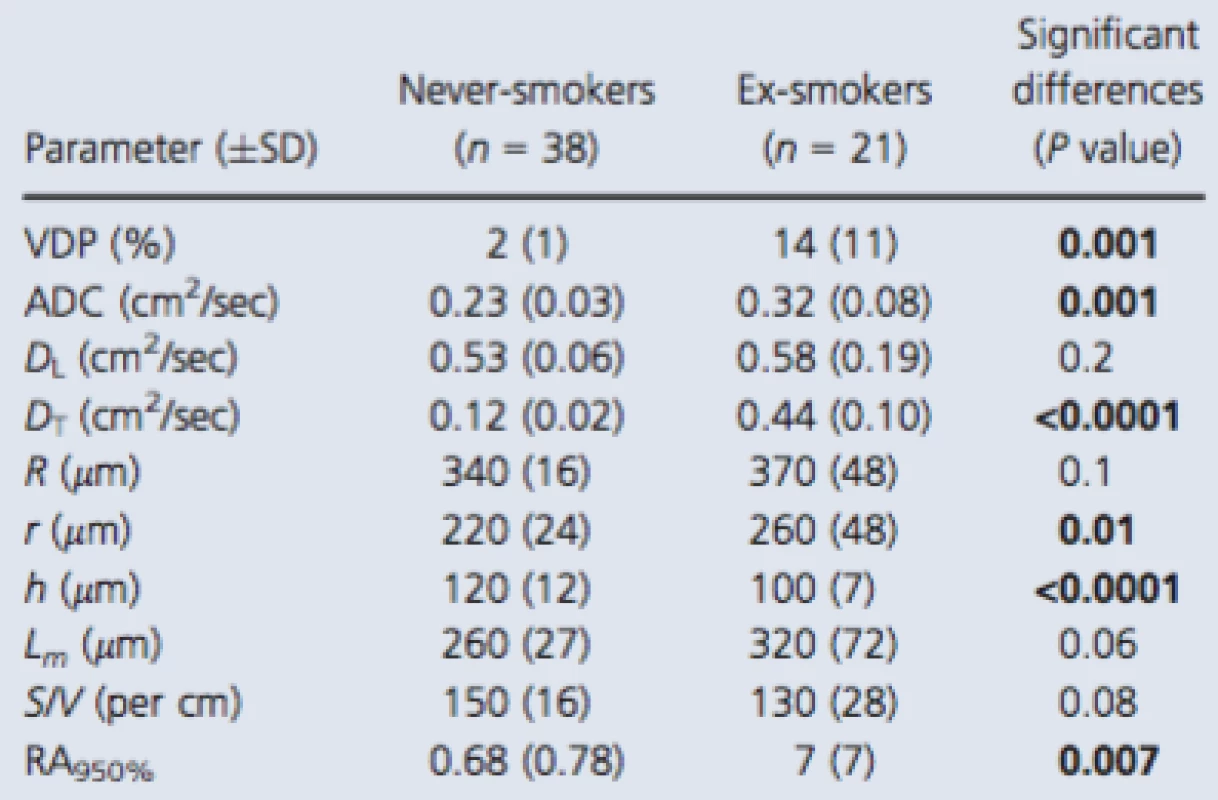
Significant differences (P value) generated using a two‐tailed t‐test and corrected using the Holm–Bonferroni method. Bold values denotes significant difference (P < 0.05). VDP, ventilation defect percent; ADC, apparent diffusion coefficient; R, external airway radius; r, internal airway radius; h, alveolar sheath; Lm, mean linear intercept; S/V, surface area‐to‐volume ratio; RA950, relative area of the CT density histogram less than −950 Hounsfield units. Figure 3 shows some of these comparisons in more detail. There were significant differences for never‐smokers compared to ex‐smokers with CT evidence of emphysema for all morphometric parameters and ADC (all P < 0.001). Never‐smokers were also significantly different than ex‐smokers without emphysema for h but not for ADC, R, r, h, Lm, or S/V. In contrast, ex‐smokers with emphysema reported significantly different ADC, R, r, Lm, S/V but not h, compared to ex ‐ smokers without emphysema.
Figure 3. <sup>3</sup>He MRI morphometry measurements. Box and whisker plots show 25–75 percentile as well as minimum and maximum values. NS = never‐smokers (n = 38); E=ex‐smokers with emphysema (n = 8); EnE = ex‐smokers with no emphysema (n = 13); ADC, apparent diffusion coefficient; R, external airway radius; r, internal airway radius; h, alveolar sheath; L<sub>m</sub>, mean linear intercept; S/V, surface area‐to‐volume ratio. Significant differences (P value) computed using a Kruskal–Wallis test with Dunn's correction. ns = not significant P > 0.05; *P < 0.05; **P < 0.01; ***P < 0.001; ****P < 0.0001. 
Relationships with FEV1/FVC and DLCO
Pearson correlation coefficients (Bonferroni‐corrected P values) for 3He morphometry measurements with FEV1/FVC and DLCO are shown in Table 3. For all subjects, there were relationships for DLCO and FEV1/FVC with external and internal radius, mean linear intercept, ADC, RA950, and surface area‐to‐volume ratio, but only FEV1/FVC significantly correlated with h. For never‐smokers, there were no significant correlations between the morphometry measurements and either FEV1/FVC or DLCO. In contrast, for ex‐smokers, the external airway radius (r = −0.54,P = 0.04), ADC (r = −0.74, P = 0.0008), RA950 (r = −0.87, P < 0.0001), and surface area‐to‐volume ratio (r = 0.58, P = 0.03) significantly correlated with FEV1/FVC and there were similar significant relationships with DLCO.
3. Relationship of 3He MRI morphometry with pulmonary function measurements 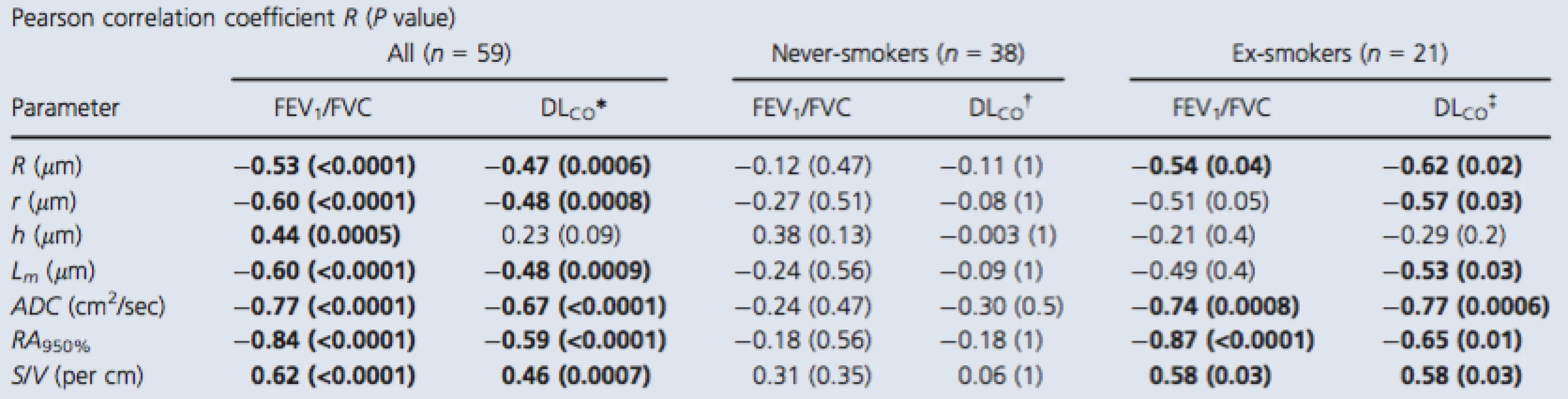
P value generated using a two‐tailed t‐test and corrected using the Holm–Bonferroni method. Bold values denotes significant difference (P < 0.05). FEV1, forced expiratory volume in 1 sec; FVC, forced vital capacity; DLCO, diffusing capacity of the lung for carbon monoxide percent predicted; R, external airway radius; r, internal airway radius; h, alveolar sheath; Lm, mean linear intercept; ADC, apparent diffusion coefficient; RA950, relative area less than −950 HU; S/V, surface area‐to‐volume ratio. *n = 56, †n = 36, ‡n = 20. Discussion
To better understand the changes in the lung parenchyma that accompany aging, we generated and evaluated noninvasive in vivo MRI estimates of acinar duct and alveolar dimensions in elderly never‐smokers and smokers. We made the following observations: (1) elderly never‐smokers reported diminished internal airway radius and greater alveolar depth compared to elderly ex‐smokers; (2) ex‐smokers with and without emphysema were significantly different for ADC, external and internal airway radius, mean linear intercept, and surface area‐to‐volume ratio but not alveolar depth; (3) there was a significant difference for alveolar depth for never‐smokers and ex‐smokers without emphysema, in whom all other morphological measures and ADC were not significantly different; and (4) in elderly never‐smokers, there were no significant correlations, whereas in elderly ex‐smokers, FEV1/FVC and DLCO significantly correlated with ADC, RA950, R, and S/V, while DLCOalso significantly correlated with r and Lm.
Differences between never ‐ and ex‐smokers
As expected, the vast majority of elderly never‐smokers reported normal pulmonary function measurements. While two never‐smokers reported FEV1/FVC values less than (but very close to) the GOLD threshold for COPD, there were no occupational or second hand smoke exposures that could explain these findings. When compared to literature reported values for younger never‐smokers, we observed elevated ADC (0.23 cm2/s vs. 0.17 cm2/s) (Fain et al. 2006), diminished alveolar depth (120 vs. 130 μm), and elevated Lm (260 vs. 240 μm) (Quirk et al. 2015) in the elderly never‐smokers. These findings may be attributed to a loss of elastin or change in collagen content, organization, and/or distribution with age (West 1971; Sobin et al. 1988). Moreover, these differences may also be explained by inflammation/edema or fibrosis, although there is no evidence to suggest this in any of the subgroups studied here.
The acinar morphometric measurements in elderly never‐smokers were also significantly different compared to the ex‐smokers with emphysema, but when compared to ex‐smokers without emphysema, only alveolar depth was significantly different. The finding of elevated ADC and some morphometric measures in ex‐smokers was also supported by the finding of abnormally elevated RA950 measurements. As shown in schematic in Figure 4, elderly ex‐smokers reported diminished alveolar depth and S/V as well as greater Lm as compared to never‐smokers. There are several potential mechanisms for these findings including the fact that emphysematous enlargement of the acinar ducts can result in flattening of the alveolus and retraction of the alveolar septa (Hartroft 1945).
Figure 4. Alveolar duct schematic. Acinar duct and alveolar morphological parameters were based on Weibel model (Weibel 1963) for acinar duct parameters shown for a representative young never‐smoker (Quirk et al. 2015), elderly never‐smoker, and elderly never‐smoker with and without emphysema. 
It is also important to point out that there were differences between ex‐smokers with and without emphysema and the elderly never‐smokers. While ADC, external radius, internal radius, mean linear intercept, and surface area‐to‐volume ratio differed were different between ex‐smokers with and without emphysema, this was not the case for never‐smokers and the ex‐smokers without emphysema in whom only alveolar depth differed. We observed no significant difference in alveolar depth between ex‐smokers with (mean h = 100 μm) and without (mean h = 110 μm) emphysema; this diminished h value was not sufficient to detect significant differences between the two groups of ex‐smokers. There were, however, significant differences in ADC and all other morphometric measurements.
We must acknowledge the sample sizes for ex‐smokers with and without emphysema are different and this is a study limitation. However, we thought it was important to point out the heterogeneity of emphysema in these volunteers. Although this is a very small subgroup to evaluate, it helps explain parenchyma differences due to lung aging relative to smoking; these comparisons also provide motivation for a larger study in ex‐smokers with COPD. We think these are important clues that point to the differences between senile emphysema and the mild emphysema that is coincident with tobacco smoke exposure.
Relationships between morphometric and pulmonary function measurements
In all participants, there were moderate and strong relationships between all morphological measurements, RA950 and ADC with FEV1/FVC, wheras DLCO had no relationship with h but related to all other morphological measurements, RA950, and ADC, and this provides a way to internally validate the MRI estimates and their clinical relevance. In the elderly never‐smokers, neither FEV1/FVC nor DLCO had any significant relationship with ADC, RA950, or any of the morphological measurements. The lack of significant relationships between acinar morphological estimates and DLCO in elderly never‐smokers was not surprising, but the finding of significantly different morphometric measurements in the presence of normal DLCO was somewhat unexpected and may underscore the sensitivity of MRI to acinar duct geometries. At the same time, normal RA950 values in the presence of “elevated” Lm may also provide strong evidence of the sensitivity of MRI to very mild emphysema even when CT is normal. The mean Lm value obtained for older never‐smokers was 5% larger than reported previously (240–250 μm) (Quirk et al. 2015), this may be due to the 10‐year age difference between these subjects. The elevated mean Lm value may reflect normal lung aging (a loss of elastin or change in collagen content) over the 10‐year period.
Considerations and limitations
We must acknowledge a number of study limitations including the fact that 3He MRI requires unique expertise and equipment. There is an extremely limited supply of helium gas, making further follow‐up studies and clinical implementation of this technique unlikely. One common limitation of the multiple b‐value method is the relatively long data acquisition time (i.e., longer than typical breath‐hold durations) and typically lower SNR compared to the more commonly used two b‐value ADC method (due to the larger number of RF pulses). To overcome these inherent limitations, parallel imaging was previously piloted in asthma patients (Chang et al. 2015). This previous work was similar to our approach, whereby 3D whole‐lung morphometry data were acquired based on 5 bvalues during a single 15‐sec breath‐hold, with adequate spatial resolution (Chang et al. 2015). By combining our approach with parallel imaging, further reductions in acquisition time and improved spatial resolution and/or SNR can be achieved.
It is also important to acknowledge that there is still room for improvement in the computational modeling of pulmonary morphometry. Algorithm optimization is still required but MRI is more time efficient and less invasive than lung stereology. However, MRI morphometry still requires manual observer interaction and is computationally intense. Moreover, although the morphological equations we used were appropriate for healthy and mildly emphysematous lungs, when acinar morphologies deviate significantly from these structures, as in the case of severe emphysema or bronchopulmonary dysplasia, the “cylindrical” (Yablonskiy et al. 2002) and “branching” models (Parra‐Robles et al. 2010; Parra‐Robles and Wild 2012) may not be appropriate. The morphometry model also has limitations, but to our knowledge this is the only available model in the literature providing mathematical equations for the extraction of lung microstructure parameters. Using this model, the correspondence between MRI‐based Lm estimates and the histological mean linear intercept (MLI) estimates was also confirmed previously (Yablonskiy et al. 2014). Other limitations originating from the morphometry model itself were also described previously (Parra‐Robles et al.2010; Parra‐Robles and Wild 2012). We compared diffusion MRI measurements obtained at 3 T and 1.5 T because previously published work suggested that ADC values and morphometric parameters may be overestimated at higher magnetic fields (Parra‐Robles et al. 2012a). To investigate the effect of field strength we conducted a substudy in young never‐smokers (mean age = 22 years, data not shown) and obtained ADC values for five of these never‐smokers and morphometric parameters for one of them. The ADC estimates at 3 T (mean = 0.172 cm2/s) were in agreement with ADC values (mean = 0.178 cm2/s) (Fain et al. 2006) obtained at 1.5 T using ∆ = 1.46 msec and the same diffusion gradient waveform and scanner platform (GEHC, trapezoidal pulses with 500 μsec ramp times, 460 μsec peak pulse width, and 1.94848 G/cm peak pulse amplitude, b = 1.6 sec/cm2). In addition, the morphometry results for a single young subject (Lm = 195 μm) was within the range of Lm values (180–220 μm) observed at 1.5 T (Quirk et al.2015).
While generally smaller ADC values for never‐smokers were reported at 1.5 T (Swift et al. 2005) using the same diffusion time (1.46 msec) and diffusion gradient waveform, there previous results are not directly comparable to what we report because these data stem from younger never‐smokers (mean = 52 years of age) and additionally, the b value was almost twice as large (2.86 sec/cm2). Both of these issues would influence ADC to lower values. At the same time, the ADC for never‐smokers were in agreement with previously published values obtained at 1.5 T (Fain et al. 2006). Another limitation stems from the assumption at the foundation of the diffusion/morphometry relationship which presumes that the diffusing gas atoms cannot penetrate through alveolar walls. Alveolar walls have pores, although their effects on DL and DT are considered negligible in healthy adults due to the small number of microscopic (<10 μm) pores present (Nagai et al. 1995). In elderly and emphysematous lung, however, this assumption likely weakens, as more pores of variable size (>20 μm) are present, ultimately increasing the transverse and longitudinal ADC values (Nagai and Thurlbeck 1991). Another drawback stems from the fact that an enormous amount of data is reduced to a few parameters of an extremely simplified whole‐lung average anatomic model of the acini and that valuable information on gross differences in topographical heterogeneity may be neglected. In this regard, we note however that gross differences in topographical heterogeneity were explored using CT and we did not find such gross in these participants – though this is a common feature in more advanced COPD. Finally, it should be noted that a diffusion time of 1.46 msec was used in order to enable comparisons with previous measurements made in the same subjects. Based on theoretical predictions (Yablonskiy et al.2009), the optimal diffusion time in human lungs using 3He MRI is 1.6–1.8 msec and therefore the use of a smaller diffusion time may lead to overestimates of morphometric parameters (Parra‐Robles et al. 2012b). Nevertheless, any potential overestimation of R and r due to the 8% smaller ∆would be quite minor and not change the conclusions of this study.
Conclusions
This is the first study to implement noninvasive in vivo MRI morphometry in a relatively large group of elderly volunteers with and without a history of tobacco smoking that aimed to provide a better understanding of the parenchyma changes that accompany lung aging and smoking. This study showed that there are significant but small differences in never ‐ and ex‐smokers in acinar duct internal radius and alveolar depth and demonstrated the sensitivity of MRI noninvasive measurements of pulmonary microstructure to dissect the effects of smoking and aging on acinar morphometry.
Conflict of Interest
None declared.
supplemental Data
Table S1. Subject listing of demographics.
Table S2. Subject listing of MRI morphometry data. [phy212583-sup-0001-TableS1-S2.docx]
Acknowledgments
We thank S. Blamires for clinical coordination, A. Wheatley for gas contrast administration, and T. Szekeres for MRI of research volunteers.
Footnotes
-
Funding Information
G. Parraga gratefully acknowledges support from a Canadian Institutes of Health Research (CIHR) New Investigator Award and ongoing research funding from CIHR Operating Grant MOP 106437.
- Manuscript Received: September 13, 2015.
- Manuscript Accepted: September 21, 2015.
Correspondence
Grace Parraga, Robarts Research Institute, 1151 Richmond St N, London, Canada, N6A 5B7.
Tel: 519‐913‐5265
E‐mail: gparraga@robarts.ca
Sources
1. Altes, T. A., J. Mata, E. E. de Lange, J. R. Brookeman, and J. P. 3rd Mugler. 2006. Assessment of lung development using hyperpolarized helium-3 diffusion MR imaging. J. Magn. Reson. Imaging 24 : 1277–1283.
2. Chang, Y. V., J. D. Quirk, M. Castro, and D. A. Yablonksiy. 2015. Single breath-hold, whole lung morphometry with hyperpolarized 3he using parallel imaging (Abstract). In: International Society for Magnetic Resonance in Medicine Annual Scientific Meeting, Wednesday June 3rd, 2015. Toronto, Canada.
3. Diaz, S., I. Casselbrant, E. Piitulainen, P. Magnusson, B. Peterson, P. Wollmer, et al. 2009. Validity of apparent diffusion coefficient hyperpolarized 3He-MRI using MSCT and pulmonary function tests as references. Eur. J. Radiol. 71 : 257–263.
4. Evans, A., D. McCormack, A. Ouriadov, R. Etemad-Rezai, G. Santyr, and G. Parraga. 2007. Anatomical distribution of 3He apparent diffusion coefficients in severe chronic obstructive pulmonary disease. J. Magn. Reson. Imaging 26 : 1537–1547.
5. Fain, S. B., T. A. Altes, S. R. Panth, M. D. Evans, B. Waters, J. P. 3rd Mugler, et al. 2005. Detection of age-dependent changes in healthy adult lungs with diffusion-weighted 3He MRI. Acad. Radiol. 12 : 1385–1393.
6. Fain, S. B., S. R. Panth, M. D. Evans, A. L. Wentland, J. H. Holmes, F. R. Korosec, et al. 2006. Early emphysematous changes in asymptomatic smokers: detection with 3He MR imaging. Radiology 239 : 875–883.
7. Fletcher, C., and R. Peto. 1977. The natural history of chronic airflow obstruction. Br. Med. J. 1 : 1645–1648.
8. Frank, N. R., J. Mead, and B. G. Jr Ferris. 1957. The mechanical behavior of the lungs in healthy elderly persons. J. Clin. Investig. 36 : 1680–1687.
9. Gevenois, P. A., P. De Vuyst, V. de Maertelaer, J. Zanen, D. Jacobovitz, M. G. Cosio, et al. 1996. Comparison of computed density and microscopic morphometry in pulmonary emphysema. Am. J. Respir. Crit. Care Med. 154 : 187–192.
10. Hartroft, W. S. 1945. The microscopic diagnosis of pulmonary emphysema. Am. J. Pathol. 21 : 889–903.
11. Hogg, J. C. 2004. Pathophysiology of airflow limitation in chronic obstructive pulmonary disease. Lancet 364 : 709–721.
12. Janssens, J. P., J. C. Pache, and L. P. Nicod. 1999. Physiological changes in respiratory function associated with ageing. Eur. Respir. J. 13 : 197–205.
13. Kirby, M., L. Mathew, A. Wheatley, G. E. Santyr, D. G. McCormack, and G. Parraga. 2010. Chronic obstructive pulmonary disease: longitudinal hyperpolarized (3)He MR imaging. Radiology 256 : 280–289.
14. Kirby, M., M. Heydarian, S. Svenningsen, A. Wheatley, D. G. McCormack, R. Etemad-Rezai, et al. 2012. Hyperpolarized 3He magnetic resonance functional imaging semiautomated segmentation. Acad. Radiol. 19 : 141–152.
15. Kronenberg, R. S., and C. W. Drage. 1973. Attenuation of the ventilatory and heart rate responses to hypoxia and hypercapnia with aging in normal men. J. Clin. Invest. 52 : 1812.
16. Laennec, R. T. H., and J. Forbes. 1834. A treatise on the diseases of the chest, and on mediate auscultation. Thomas & George Underwood, London.
17. Mathew, L., A. Evans, A. Ouriadov, R. Etemad-Rezai, R. Fogel, G. Santyr, et al. 2008. Hyperpolarized 3 He magnetic resonance imaging of chronic obstructive pulmonary disease: reproducibility at 3.0 Tesla. Acad. Radiol. 15 : 1298 – 1311.
18. Mayer, E., C. Blazsik, and I. Rappaport. 1958. Emphysema and the lungs of the aged: a clinical studypreliminary report. Chest 34 : 247–256.
19. Miller, G., T. Altes, J. Brookeman, E. De Lange, and J. Mugler Iii. 2004. Hyperpolarized 3He lung ventilation imaging with B 1-inhomogeneity correction in a single breath-hold scan. Magn. Reson. Mater. Phys., Biol. Med. 16 : 218–226.
20. Miller, M. R., J. Hankinson, V. Brusasco, F. Burgos, R. Casaburi, A. Coates, et al. 2005. Standardisation of spirometry. Eur. Respir. J. 26 : 319–338.
21. Nagai, A., and W. M. Thurlbeck. 1991. Scanning electron microscopic observations of emphysema in humans. A descriptive study. Am. Rev. Respir. Dis. 144 : 901–908.
22. Nagai, A., W. M. Thurlbeck, and K. Konno. 1995. Responsiveness and variability of airflow obstruction in chronic obstructive pulmonary disease. Clinicopathologic correlative studies. Am. J. Respir. Crit. Care Med. 151 : 635 – 639.
23. Ouriadov, A. V., W. W. Lam, and G. E. Santyr. 2009. Rapid 3 - D mapping of hyperpolarized 3He spin-lattice relaxation times using variable flip angle gradient echo imaging with application to alveolar oxygen partial pressure measurement in rat lungs. Magn. Reson. Mater. Phys., Biol. Med. 22 : 309 –
24. 318.Ouriadov, A., A. Farag, M. Kirby, D. G. McCormack, G.
25. Parraga, and G. E. Santyr. 2013. Lung morphometry using hyperpolarized 129Xe apparent diffusion coefficient anisotropy in chronic obstructive pulmonary disease. Magn. Reson. Med. 70 : 1699–1706.
26. Ouriadov, A., A. Farag, M. Kirby, D. McCormack, G. Parraga, and G. Santyr. 2014. Pulmonary hyperpolarized 129Xe morphometry for mapping xenon gas concentrations and alveolar oxygen partial pressure: proof-of-concept demonstration in healthy and COPD subjects. Magn. Reson. Med. doi: 10.1002/mrm.25550.
27. Ouriadov, A., M. Fox, E. Hegarty, G. Parraga, E. Wong, and G. E. Santyr. 2015. Early stage radiation-induced lung injury detected using hyperpolarized Xe Morphometry: proof-of - concept demonstration in a rat model. Magn. Reson. Med. doi: 10.1002/mrm.25825.
28. Parraga, G., A. Ouriadov, A. Evans, S. McKay, W. W. Lam, A. Fenster, et al. 2007. Hyperpolarized 3He ventilation defects and apparent diffusion coefficients in chronic obstructive pulmonary disease: preliminary results at 3.0 Tesla. Invest. Radiol. 42 : 384–391.
29. Parraga, G., L. Mathew, R. Etemad-Rezai, D. G. McCormack, and G. E. Santyr. 2008. Hyperpolarized 3He magnetic resonance imaging of ventilation defects in healthy elderly volunteers: initial findings at 3.0 Tesla. Acad. Radiol. 15 : 776–785.
30. Parra-Robles, J., and J. M. Wild. 2012. The influence of lung airways branching structure and diffusion time on measurements and models of short-range 3He gas MR diffusion. J. Magn. Reson. 225 : 102–113.
31. Parra-Robles, J., S. Ajraoui, M. Deppe, S. Parnell, and J. Wild. 2010. Experimental investigation and numerical simulation of 3 He gas diffusion in simple geometries: implications for analytical models of 3 He MR lung morphometry. J. Magn. Reson. 204 : 228–238.
32. Parra-Robles, J., S. Ajraoui, H. Marshall, M. H. Deppe, X. Xu, and J. M. Wild. 2012a. The influence of field strength on the apparent diffusion coefficient of 3He gas in human lungs. Magn. Reson. Med. 67 : 322–325.
33. Parra-Robles, J., M. Deppe, X. Xiaojun, M. Helen, and J. M. Wild. 2012b. The influence of diffusion time on the measurement of the short-range 3He diffusivity in human lungs (Abstract). In: International Society for Magnetic Resonance in Medicine Annual Scientific Meeting, Wednesday May 9th, 2012. Melbourne, Australia.
34. Peterson, D. D., A. I. Pack, D. A. Silage, and A. P. Fishman. 1981. Effects of aging on ventilatory and occlusion pressure responses to hypoxia and hypercapnia. Am. Rev. Respir. Dis. 124 : 387–391.
35. Quirk, J. D., B. A. Lutey, D. S. Gierada, J. C. Woods, R. M. Senior, S. S. Lefrak, et al. 2011. In vivo detection of acinar microstructural changes in early emphysema with 3He lung morphometry. Radiology 260 : 866–874.
36. Quirk, J. D., Y. V. Chang, and D. A. Yablonskiy. 2015. In vivo lung morphometry with hyperpolarized (3) He diffusion MRI: reproducibility and the role of diffusion - sensitizing gradient direction. Magn. Reson. Med. 73 : 1252 – 1257.
37. Rose, A. 1948. The sensitivity performance of the human eye on an absolute scale. J. Opt. Soc. Am. 38 : 196–208.
38. Salerno, M., E. E. de Lange, T. A. Altes, J. D. Truwit, J. R. Brookeman, and J. P. Mugler. 2002. Emphysema: hyperpolarized helium 3 diffusion MR imaging of the lungs compared with spirometric indexes—initial experience 1. Radiology 222 : 252–260.
39. Sharma, G., and J. Goodwin. 2006. Effect of aging on respiratory system physiology and immunology. Clin. Interv. Aging 1 : 253–260.
40. Sobin, S. S., Y. C. Fung, and H. M. Tremer. 1988. Collagen and elastin fibers in human pulmonary alveolar walls. J. Appl. Physiol. 64 : 1659–1675.
41. Sukstanskii, A. L., and D. A. Yablonskiy. 2008. In vivo lung morphometry with hyperpolarized 3He diffusion MRI: theoretical background. J. Magn. Reson. 190 : 200–210.
42. Swift, A. J., J. M. Wild, S. Fichele, N. Woodhouse, S. Fleming, J. Waterhouse, et al. 2005. Emphysematous changes and normal variation in smokers and COPD patients using diffusion 3He MRI. Eur. J. Radiol. 54 : 352–358.
43. Thurlbeck, W. M. 1967. Internal surface area and other measurements in emphysema. Thorax 22 : 483 – 496.
44. Turner, J. M., J. Mead, and M. E. Wohl. 1968. Elasticity of human lungs in relation to age. J. Appl. Physiol. 25 : 664 – 671.
45. Verbeken, E, M. Cauberghs, I. Mertens, J. Clement, J. Lauweryns, and Van de Woestijne K. 1992. The senile lung. Comparison with normal and emphysematous lungs. 1. Structural aspects. CHEST J. 101 : 793–799.
46. Weibel, E. R. 1963. Geometry and dimensions of airways of conductive and transitory zones. Springer, Berlin.
47. West, J. B. 1971. Distribution of mechanical stress in the lung, a possible factor in localisation of pulmonary disease. Lancet 1 : 839–841.
48. Woods, J. C., C. K. Choong, D. A. Yablonskiy, J. Bentley, J. Wong, J. A. Pierce, et al. 2006. Hyperpolarized 3He diffusion MRI and histology in pulmonary emphysema. Magn. Reson. Med. 56 : 1293–1300.
49. Yablonskiy, D. A., A. L. Sukstanskii, J. C. Leawoods, D. S. Gierada, G. L. Bretthorst, S. S. Lefrak, et al. 2002. Quantitative in vivo assessment of lung microstructure at the alveolar level with hyperpolarized 3He diffusion MRI. Proc Natl Acad Sci U S A 99 : 3111–3116.
50. Yablonskiy, D. A., A. L. Sukstanskii, J. C. Woods, D. S. Gierada, J. D. Quirk, J. C. Hogg, et al. 2009. Quantification of lung microstructure with hyperpolarized 3He diffusion MRI. J. Appl. Physiol. 107 : 1258–1265.
51. Yablonskiy, D. A., A. L. Sukstanskii, and M. S. Conradi. 2014. Commentary on “The influence of lung airways branching structure and diffusion time on measurements and models of short-range 3He gas MR diffusion”. J. Magn. Reson. 239 : 139–142.
52. Young, R. C. Jr, D. L. Borden, and R. E. Rachal. 1987. Aging of the lung: pulmonary disease in the elderly. Age 10 : 138–145.
Article was published inPhysiological Reports

2015 Issue 10-
All articles in this issue
- S100B and NSE serum concentrations after simulated diving in rats
- The non-antibiotic macrolide EM900 inhibits rhinovirus infection and cytokine production in human airway epithelial cells
- Noninvasive quantification of alveolar morphometry in elderly never- and ex-smokers
- Subtle modulation of ongoing calcium dynamics in astrocytic microdomains by sensory inputs
- Caffeine and contraction synergistically stimulate 5′‐AMP‐activated protein kinase and insulin‐independent glucose transport in rat skeletal muscle
- PGC‐1 isoforms and their target genes are expressed differently in human skeletal muscle following resistance and endurance exercise
- Physiological Reports
- Journal archive
- Current issue
- Online only
- About the journal
Most read in this issue- S100B and NSE serum concentrations after simulated diving in rats
- Subtle modulation of ongoing calcium dynamics in astrocytic microdomains by sensory inputs
- The non-antibiotic macrolide EM900 inhibits rhinovirus infection and cytokine production in human airway epithelial cells
- Noninvasive quantification of alveolar morphometry in elderly never- and ex-smokers
Login#ADS_BOTTOM_SCRIPTS#Forgotten passwordEnter the email address that you registered with. We will send you instructions on how to set a new password.
- Career








