-
Medical journals
- Career
Metoda měření poddajnosti a těsnosti modelů respirační soustavy pacienta
: Karel Roubík; Monika Stránská
: Czech Technical University in Prague, Faculty of Biomedical Engineering, Kladno, Czech Republic
: Lékař a technika - Clinician and Technology No. 1, 2014, 44, 9-18
: Original research
Článek se zabývá návrhem a ověřením prakticky použitelné metody určování poddajnosti modelů respirační soustavy. Kromě existujících typů poddajností izotermické a adiabatické je v této studii zaveden pojem efektivní poddajnosti respirační soustavy. V práci je dále popsán test těsnosti modelů. Všechny popsané metody byly otestovány na sadě nekompenzovaných i kompenzovaných rigidních modelů respirační soustavy jakož i na aktivním i pasivním modelu respirační soustavy s nastavitelnou poddajností.
Klíčová slova:
model respirační soustavy, poddajnost, efektivní poddajnost, adiabatická poddajnost, izotermická poddajnostÚvod
Mechanické vlastnosti respirační soustavy hrají důležitou roli jak v diagnostice plicního postižení, tak při optimalizaci respirační terapie v případě respirační insuficience či respiračního selhání. Většina ventilačních režimů se mechanickým parametrům respirační soustavy přizpůsobuje a moderní ventilační režimy jsou na základě plicní mechaniky v reálném čase upravovány tak, aby umělá plicní ventilace na jedné straně zajišťovala dostatečnou a stabilní výměnu plynů a na druhé straně nedocházelo k mechanickému poškození plic, což patří mezi hlavní adversní účinky umělé plicní ventilace.
Při vývoji ventilační techniky, jejím testování a kalibracích, při vývoji nových ventilačních režimů, při studiu interakce pacienta s ventilátorem, při výcviku respiračních terapeutů a při mnoha dalších aplikacích jsou s výhodou používány fyzikální modely respirační soustavy. Ne vždy lze totiž uvedené testy provádět na pacientech a z hlediska ekonomického i etického bývají problematické i studie na zvířatech. Navíc při ověřování a kalibracích ventilační techniky je nutné použít model se stálými a dobře definovanými mechanickými parametry, což biologické objekty, narozdíl od fyzikálních modelů, nesplňují.
V praxi se můžeme setkat s mnoha typy modelů respirační soustavy, které se liší účelem použití, složitostí jejich konstrukce a přesností, s jakou simulují mechanické vlastnosti respirační soustavy pacienta. Fyzikální modely respirační soustavy jsou však též přístroje, které byly navrženy a zkonstruovány dle určitých požadavků a simulující mechanické parametry respirační soustavy vždy jen v určitém rozsahu. Jejich chování se též může lišit při různých ventilačních režimech. Velmi významné odchylky lze očekávat při nekonvenčních ventilačních režimech, mezi které patří všechny druhy vysokofrekvenční umělé plicní ventilace, ventilace helioxem apod., díky jejich odlišnostem od ventilace konvenční, pro kterou bývají modely respirační soustavy zpravidla konstruovány.
Poddajnost označovaná Crs je jedním ze základních mechanických parametrů respirační soustavy, který je ovlivněn patologickými změnami respirační soustavy. Udává, jak snadno je soustava schopná hromadit dodávaný plyn. Hromadění plynu způsobuje nárůst tlaku uvnitř soustavy. Při snadné inflaci soustavy, kde v ní vzniká relativně malý přírůstek tlaku, se jedná o soustavu velmi poddajnou, tedy má velkou poddajnost. Naopak soustava, u které i malý dodaný objem plynu způsobí relativně velký nárůst tlaku, je soustava tuhá, nepoddajná, mající malou hodnotu poddajnosti. Fyzikální veličina poddajnost C je definována jako přírůstek dodávaného objemu plynu ∆V při jednotkovém navýšení tlaku ∆p [1]:
∆ V
C = ---------
∆ p
(1)Jednotkou poddajnosti je m3/Pa, v respirační péči se však používají jednotky L/kPa nebo ještě častěji mL/cm H2O.
Nejjednodušší fyzikální model poddajnosti respirační soustavy je rigidní nádoba o známém objemu. Jako rigidní model se často používá skleněný demižon. U tohoto modelu se dá poddajnost vypočítat jako poměr objemu V nádoby k atmosférickému tlaku patm :
V
C = ---------
patm
(2)Zde ale narážíme na problém při rychlém plnění nádoby plynem. Při rychlém plnění se plyn ohřívá a tepelně roztahuje (adiabatický děj), tedy při stejném dodaném objemu vzniká vyšší tlak než po vyrovnání teplot s okolím (tj. analogii s izotermickým dějem). Vzhledem k tomu, že budeme demižón ventilovat, musíme vypočítanou poddajnost podle vzorce (2) vydělit adiabatickou konstantou κ. Výsledný vzorec bude mít tvar [1]:
V
C = ------------
patm · κ
(3)Dalšími možnostmi realizace fyzikálního modelu poddajnosti respirační soustavy jsou různé měchy a vaky. Jsou však vyrobeny z materiálu, jehož vlastnosti se mění v čase, proto se tyto modely nepoužívají ke kalibracím. Používají se často v iniciální fázi ventilace, kdy se nastavuje ventilační režim a kontroluje funkčnost systému, než je připojen pacient. Příkladem tohoto modelu respirační soustavy je model Dual Adult Test Lung 5600i (Michigan Instruments, Grand Rapids, MI, USA). Mechanický model 5600i je složen ze dvou kompartmentů, které jsou tvořeny měchy, do kterých proudí vzduch, ale plnění těchto měchů je regulováno pružinou. Tento systém simuluje poddajnost respirační soustavy.
U každého kompartmentu můžeme nastavit jinou hodnotu poddajnost a výsledná hodnota poddajnosti je rovna součtu jednotlivých poddajností dílčích. Odpor respirační soustavy je u tohoto modelu realizován vložením modelu odporu respirační soustavy do vývodu z jednotlivých kompartmentů či za vývod, kde jsou kompartmenty spojené. Můžeme tedy nastavit jiný odpor u pravého či levého kompartmentu.
Příkladem elektronicky řízeného modelu plic je model ASL 5000 (IngMar Medical, Pittsburgh, PA, USA), který je složen z pístu uloženého ve válcové komoře, který je počítačově řízen dle nastavených parametrů požadované plicní mechaniky [2]. Model může pracovat v pasivním či aktivním režimu. Když je nastaven pasivní režim, model sám žádné dýchání neprovádí, ale můžeme jej ventilovat. Při aktivním režimu model sám simuluje dýchání pacienta. K ovládání tohoto modelu je potřeba software, ve kterém se nastavují parametry respirační soustavy (poddajnost plic i hrudní stěny, lineární či nelineární poddajnost, odpor parabolický i lineární…). Je možné nastavit i rozdílný odpor při inspirační a exspirační fázi dechu [3]. Vztah mezi tlakem a objemem může být i nelineární a může mít esovitý tvar stejný, jaký má fyziologická p-V křivka reálného pacienta.
Znalost skutečné hodnoty poddajnosti modelu respirační soustavy může být nepostradatelná při nejrůznějších aplikacích, přičemž její stanovování může v praxi představovat problém. Komplikací může být i nutnost odlišovat adiabatickou a izotermickou poddajnost a při stanovování hodnot těchto poddajností počítat i s vlivem netěsnosti modelu respirační soustavy, přičemž malá míra netěsnosti bývá běžná i u komerčně dostupných modelů.
Cílem této studie je návrh a ověření prakticky použitelné metody určování poddajnosti modelů respirační soustavy a testu těsnosti těchto modelů. Kromě existujících typů poddajností izotermické a adiabatické je v této studii zaveden pojem efektivní poddajnost respirační soustavy.
Metody
Metoda měření poddajnosti respirační soustavy
Pro měření poddajnosti modelů respirační soustavy byla navržena a sestavena měřicí soustava, která je složena z měřeného modelu plic, velkoobjemové kalibrační stříkačky (Hans Rudolph, inc., Shawnee, KS, USA), propojky stříkačky s modelem plic s odbočkou vybavenou Luer Lock portem a monitoru tlaku připojeného k soustavě tlakovou hadičkou přes výše zmíněný Luer Lock port. Monitor tlaku umožňuje kontinuální měření a záznam tlaku v soustavě. Jedná se o přístroj zkonstruovaný na FBMI, který obsahuje tepelně kompenzované a linearizované tlakové senzory (26PC05, Honeywell) a je založen na 12bitovém A/D převodníku DAQ NI USB-6008 (National Instruments) s nastavenou vzorkovací frekvencí 1 kHz. Sestava s napojeným senzorem tlaku je zobrazena na Obrázku 1. V laboratoři umělé plicní ventilace FBMI jsou k dispozici kalibrační stříkačky o objemech 0,5; 1; 3 a 7 litrů, přičemž pomocí nastavitelné zarážky lze u těchto kalibračních stříkaček nastavit i menší objemy, než je jejich objem maximální.
1. Sestava pro měření poddajnosti modelu respirační soustavy (v tomto případě rigidní nádoby) s napojeným senzorem tlaku. 
Před zahájením měření je do kalibrační stříkačky nasán požadovaný objem plynu a stříkačka je připojena k modelu prostřednictvím spojky s odbočkou pro měření tlaku. Přívodní hadička monitoru tlaku je v tomto okamžiku odpojená od spojky, aby byl tlak plynu v soustavě model - kalibrační stříkačka nulový. Jelikož je vstup monitoru tlaku připojen do atmosféry, je v tomto okamžiku možné vynulovat i případný offset tlaku zobrazovaný na monitoru tlaku.
Po připojení monitoru tlaku k soustavě (a případném vynulování senzoru tlaku) je zahájen záznam dat softwarem tlakového monitoru a po několikasekundové pauze je celý objem plynu ze stříkačky rychle vpraven do modelu plic. Doba injekce plynu do modelu by měla být velmi krátká, typicky pod 0,5 s. Na monitoru tlaku je sledována změna tlaku v soustavě. Nedochází-li k úniku plynu ze soustavy, dojde po určité době k ustálení hodnoty tlaku v soustavě. Tato doba ustálení závisí na druhu a konstrukci modelu a pohybuje se od jednotek sekund do několika minut.
Po ustálení tlaku v soustavě je naopak plyn nasáván zpět do kalibrační stříkačky, ale narozdíl od počáteční injekce plynu je toto nasávání záměrně pomalé a po menších dílčích objemech tak, aby se tlak v soustavě pohyboval v blízkosti nulové hodnoty, ale přitom aby nedosahoval záporných hodnot.
Udržování tlaku v kladných hodnotách zabrání průniku okolního plynu dovnitř soustavy při její případné netěsnosti. Postupným nasáváním plynu zpět do kalibrační stříkačky a následně ponecháním dostatečného času na ustálení hodnoty tlaku by měl být po určité době dosažen nulový tlak v soustavě, který se již v čase nemění.
Je-li tohoto nulového tlaku dosaženo právě při opětovném naplnění kalibrační stříkačky původním objemem plynu, soustava je těsná a při měření poddajnosti nedocházelo v soustavě k úniku plynu do okolí. Měření poddajnosti modelu je proto možné považovat za správné. Jestliže je naopak dosaženo stabilní nulové hodnoty tlaku v soustavě, ale do stříkačky by bylo možné ještě další objem plynu nasát (velikost tohoto deficitu objemu je možné odečíst na stupnici na rukojeti pístu kalibrační stříkačky), došlo při měření k úniku plynu ze soustavy a objem uniklého plynu odpovídá objemovému deficitu plynu ve stříkačce. Měření poddajnosti je za těchto podmínek nepřesné. Adiabatická hodnota a efektivní hodnota (viz níže) poddajnosti jsou v tomto případě ovlivněny únikem poměrně málo, zatímco izotermickou hodnotu poddajnosti změřenou za těchto podmínek nelze považovat za správnou.
Příklad průběhu tlaku v soustavě model – kalibrační stříkačka je uveden na Obrázku 2 pro případ těsné soustavy bez úniku plynu a na Obrázku 3 pro případ, kdy při měření nebyla soustava těsná a docházelo k úniku plynu ze soustavy.
2. Změny tlaku v dokonale těsném modelu respirační soustavy při měření jeho poddajnosti. Při měření byla použita kalibrační stříkačka o objemu 1 L a model o přibližném objemu 125 L. 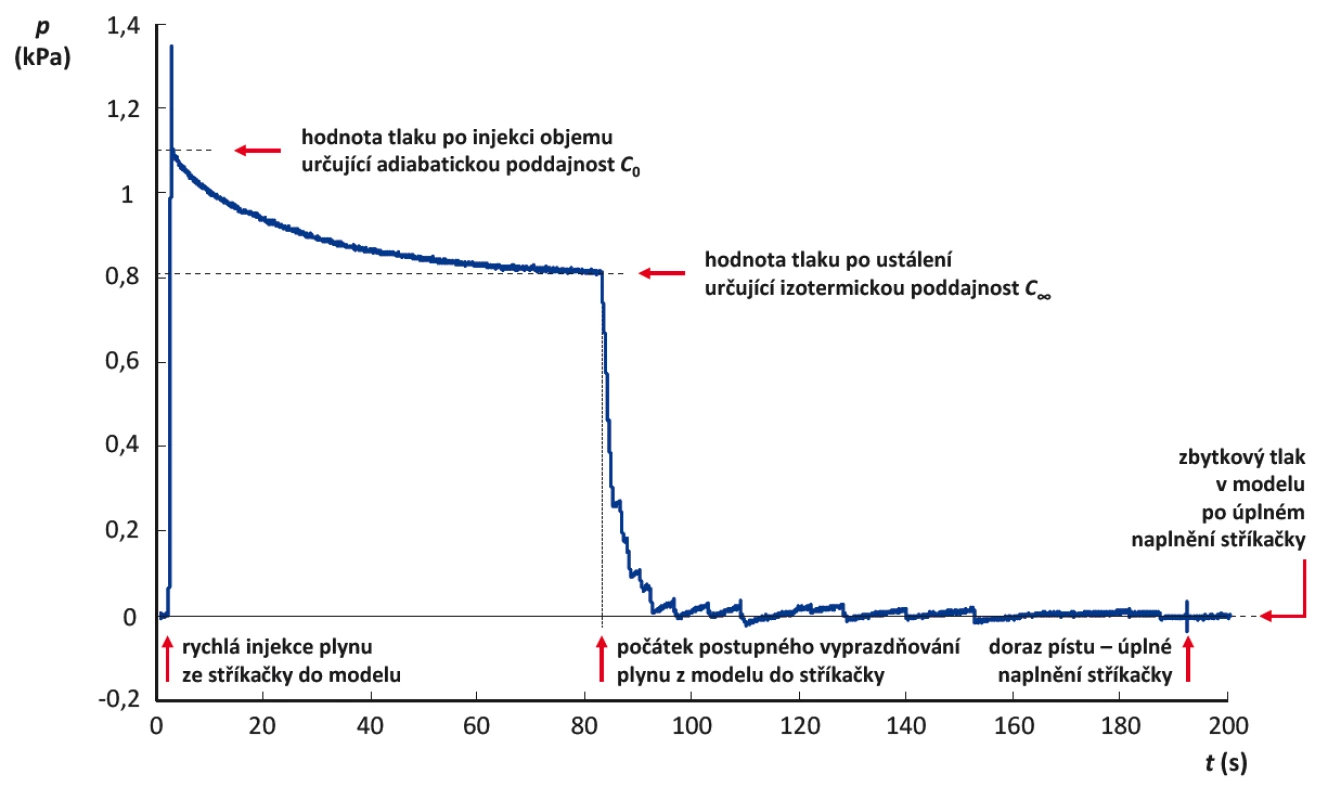
3. Změny tlaku v netěsném modelu respirační soustavy při měření jeho poddajnosti doprovázené únikem plynu ze soustavy. Při měření byla použita kalibrační stříkačka o objemu 1 L a model o přibližném objemu 100 L. 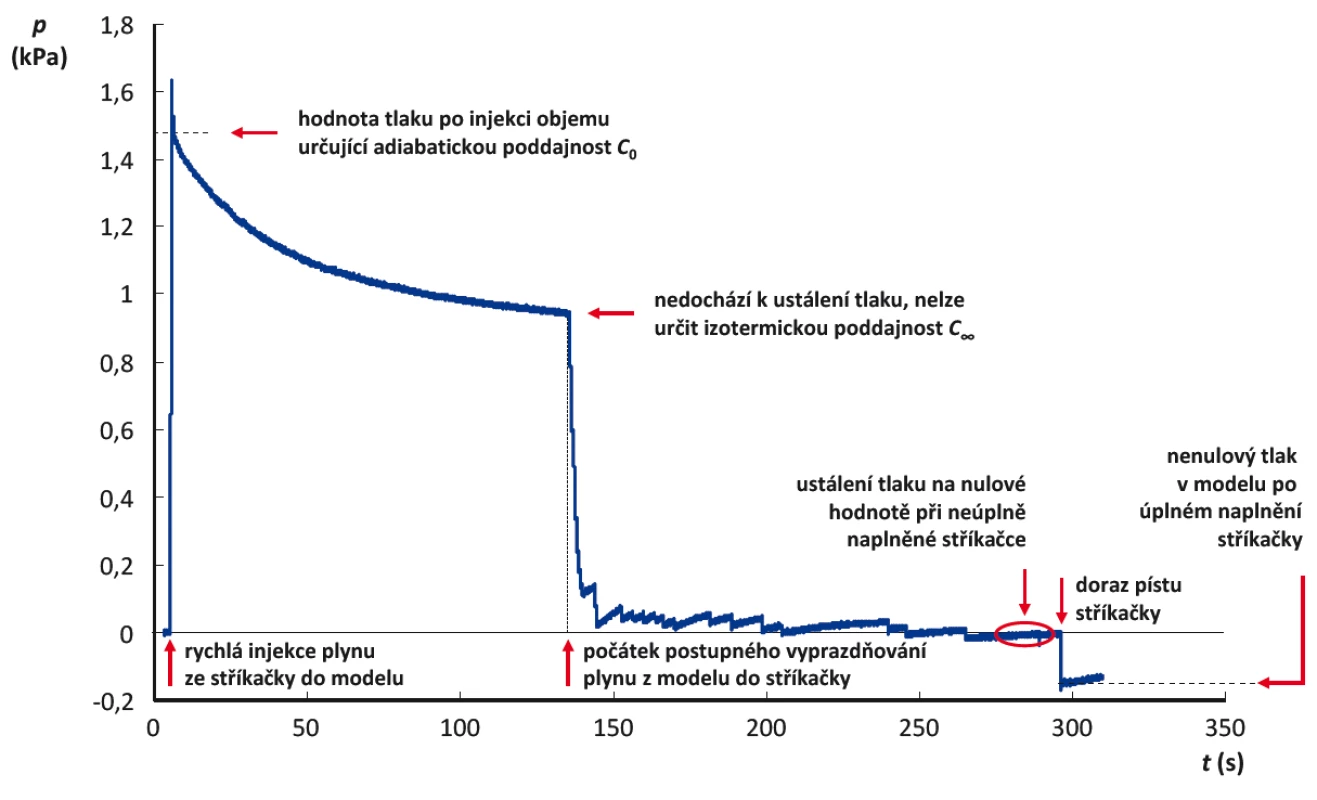
Průběh tlaku v soustavě model – kalibrační stříkačka po injekci přesně definovaného objemu plynu má exponenciálně klesající charakter. Hodnota tlaku plynu v modelu respirační soustavy v čase klesá v důsledku poklesu teploty plynu v modelu na teplotu okolí. Teplota plynu v modelu byla iniciálně zvýšena díky rychlému dodání plynu do nádoby adiabatickou kompresí plynu. Uvedený vzrůst teploty byl doprovázen i nárůstem tlaku plynu v modelu. Následně docházelo k poklesu teploty plynu v modelu na teplotu okolí a tím i k poklesu tlaku plynu v modelu. Jelikož se objem plynu v modelu neměnil, ale v modelu klesal tlak plynu, docházelo tím k nárůstu poddajnosti modelu podle vztahu (1), kde ∆ V je známý objem plynu dodaný z kalibrační stříkačky a ∆ p je změna tlaku v soustavě způsobená dodáním objemu ∆ V, v našem případě relativní tlak vůči počáteční nulové hodnotě tlaku v modelu.
Měření izotermické, adiabatické a efektivní poddajnosti modelu respirační soustavy
Poddajnost určená hodnotou tlaku bezprostředně po rychlé injekci plynu do modelu určuje adiabatickou poddajnost modelu označovanou jako C0, zatímco koncová hodnota tlaku v modelu po jeho ustálení na konstantní hodnotě určuje izotermickou poddajnost C∞. Pro lepší popis časového vývoje poddajnosti byly ještě zjišťovány poddajnosti C1 a C5 odečtené v časech 1 s a 5 s od dokončení injekce plynu. Pro další experimenty a testy modelů byla definována a ze záznamů průběhu tlaku v modelech odečtena tzv. efektivní poddajnost C0,3, určovaná v čase 0,3 s od dokončení rychlé injekce plynu do modelu. Tato hodnota byla zvolena proto, že se jedná o typickou hodnotu pro konvenční ventilaci. Režimy s inspirační pauzou okolo 0,3 s nebo režimy s dobou inspiria zhruba odpovídající tomuto času. Model respirační soustavy proto vykazoval tuto efektivní poddajnost.
Při zpětném nasávání plynu z modelu do kalibrační stříkačky dochází naopak k poklesu tlaku v modelu oproti předchozí ustálené hodnotě. Tento pokles tlaku je doprovázen poklesem teploty plynu v modelu způsobovaným adiabatickou expanzí plynu. Jelikož expanze plynu způsobuje pokles teploty plynu v modelu pod teplotu okolí, dochází při vyrovnávání teploty plynu s teplotou okolí k postupnému nárůstu tlaku v modelu, jak je patrné z Obrázku 2.
Jelikož při změně teploty plynu dochází k jeho tepelné roztažnosti, a pokud je tento plyn uzavřen např. v rigidní nádobě, dochází vlivem změn teploty k nežádoucím změnám tlaku v nádobě a tím i k chybám měření poddajnosti modelu respirační soustavy. K vyloučení vlivu teploty je proto nutné nechat model s kalibrační stříkačkou dostatečně dlouho na místě měření, aby se teploty všech částí soustavy vyrovnaly s teplotou okolí. Při vlastním měření je nutné se vyvarovat zahřívání jednotlivých částí soustavy rukama. Vhodné je i vyvarovat se přibližování těla k soustavě model – kalibrační stříkačka, protože i v tomto případě může dojít k ovlivnění teploty soustavy teplotou těla sáláním. Obdobně jako v předchozím odstavci je nutné konstatovat, že tyto teplotní vlivy mají poměrně malý vliv na přesnost stanovení adiabatické či efektivní poddajnosti, ale při měření izotermické poddajnosti je jejich vliv podstatný anebo dokonce měření izotermické poddajnosti znemožňuje.
Stanovení charakteru modelů respirační soustavy
Pro hodnocení charakteru modelu, tj. zda se model více blíží ideálnímu izotermickému modelu, nebo ideálnímu adiabatickému modelu, je pro každý z modelů spočítán polytropický koeficient a (označovaný též jako polytropický exponent), který charakterizuje děj, ke kterému při plnění modelu respirační soustavy vzduchem dochází:
C0
a = -------
C∞
(4)kde C0 je adiabatická poddajnost modelu určená hodnotou tlaku bezprostředně po injekci plynu do modelu a C∞ je izotermická poddajnost určená koncovou hodnotou tlaku v modelu po jeho ustálení na konstantní hodnotě. Vzhledem k tomu, že u některých modelů může díky netěsnostem, které nelze jednoduše odstranit, docházet k úniku plynu z modelu, není v těchto případech možné hodnotu C∞ stanovit a nelze proto určit ani hodnotu polytropického koeficientu a.
Předzpracování a zpracování naměřených dat
Kontinuální záznam tlaku byl z důvodů kompatibility se softwarem ovládajícím měřič tlaku po dokončení měření vyexportován do programu MS Excel a poté převeden do programu Matlab (MathWorks, Natick, MA, USA) k dalšímu zpracování. Záznam byl výrazně zašuměný a bylo nutné provést filtraci. K tomuto účelu byl vytvořen filtr jako kombinace mediánového filtru a dolní propusti, který byl použit na tlaková data u všech záznamů měření. Takto vyfiltrovaná data byla použita k vykreslení křivek tlaku v závislosti na čase a z těchto křivek byly odečteny hodnoty tlaku v čase 0 s; 0,3 s; 5 s a v čase, kdy došlo k ustálení tlaku. Z těchto odečtených hodnot tlaku spolu se známým objemem plynu, který byl injektován do modelu, byly vypočítány hodnoty adiabatické, efektivní a izotermické poddajnosti podle vztahu (1).
Následovalo předzpracování všech záznamů měření, aby bylo možné křivky vzájemně porovnávat a vyhodnocovat. Nejprve byly křivky posunuty v čase tak, aby okamžik dokončení injekce plynu nastal u všech záznamů ve stejném čase, což bylo zpravidla 2 s od začátku záznamu. Okamžik dokončení injekce plynu do modelu byl rozpoznán podle okamžiku, kdy hodnota tlaku dosáhla maxima. Tento okamžik byl pro účely dalšího zpracování tlakového signálu považován za čas 0 s. Následně pro usnadnění porovnávání křivek byla data normalizována. U každé křivky byla zjištěna hodnota tlaku v čase 0,3 s a všechny hodnoty tlaku dané křivky byly touto hodnotou vyděleny. Tím bylo dosaženo stavu, že v čase 0,3 s procházely všechny křivky stejným jednotkovým bodem.
Při testování modelu ASL 5000 bylo zjištěno, že odezva na změnu objemu plynu v modelu je periodická s poměrně malým tlumením. Aby bylo možné odhadnout charakter chování tohoto modelu obdobně jako u modelů ostatních, byla ze změřených signálů tlaku odstraněna periodická složka a byl tak posuzován vývoj střední hodnoty tlaku v čase. K filtraci, tj. odstranění oscilací, byl použit algoritmus vytvořený kombinací mediánového filtru vhodné délky vzhledem k frekvenci oscilací ve filtrovaném signálu a filtru typu dolní propusti.
Použité modely respirační soustavy
Hodnoty a vlastnosti poddajností modelů respirační soustavy byly měřeny na těchto modelech (v následujícím textu budou studované modely označovány v souladu s tímto seznamem):
- RN-5, RN-9, RN-12, RN-20, RN-27, RN-42, RN-54, RN-62, RN-69, RN-91 a RN-99 je celkem jedenáct nekompenzovaných modelů respirační soustavy vyrobených na FBMI z rigidních nádob (skleněné nádoby, tuhé plastové sudy) anebo jejich kombinací. Číslo označuje přibližnou velikost efektivní poddajnosti daného modelu v jednotkách mL/cm H2O. (Pozn.: Toto konečné označení uvedených modelů bylo vytvořeno teprve po zjištění jejich efektivních poddajností, tj. na základě výsledků uvedených v kapitole výsledky. Do té doby byly uvedené modely pracovně označovány přibližnými hodnotami jejich objemů podle údajů výrobce.)
- TK-38 – termokompenzovaný model vyrobený na FBMI ze dvou nádob obsahujících chomáče tenkého měděného smaltovaného drátu.
- DuraLung-4L – komerčně dostupný termokompenzovaný model DuraLung o objemu 4 L (South Pacific Biomedical, Temecula, CA, USA).
- Michigan – komerčně dostupný model Dual Adult Test Lung 5600i (Michigan Instruments, Grand Rapids, MI, USA) s nastavitelnou hodnotou poddajnosti.
- ASL 5000 – komerčně dostupný model ASL 5000 (IngMar Medical, Pittsburgh, PA, USA) s nastavitelnou hodnotou poddajnosti.
Výsledky
Před měřením poddajnosti všech výše uvedených modelů a před zjišťováním charakteru jejich chování byl proveden test těsnosti podle postupu uvedeného v metodách. Výsledky testů těsnosti jsou uvedeny graficky na Obrázku 4. Z obrázku je patrné, že u značné části rigidních modelů RN dochází k úniku plynu, díky němuž nedochází k ustálení tlaku v modelu na konstantní hodnotě a tlak v modelu neustále (až na výjimky) pomalu klesá.
4. Výsledek prvotního testu těsnosti modelů respirační soustavy. 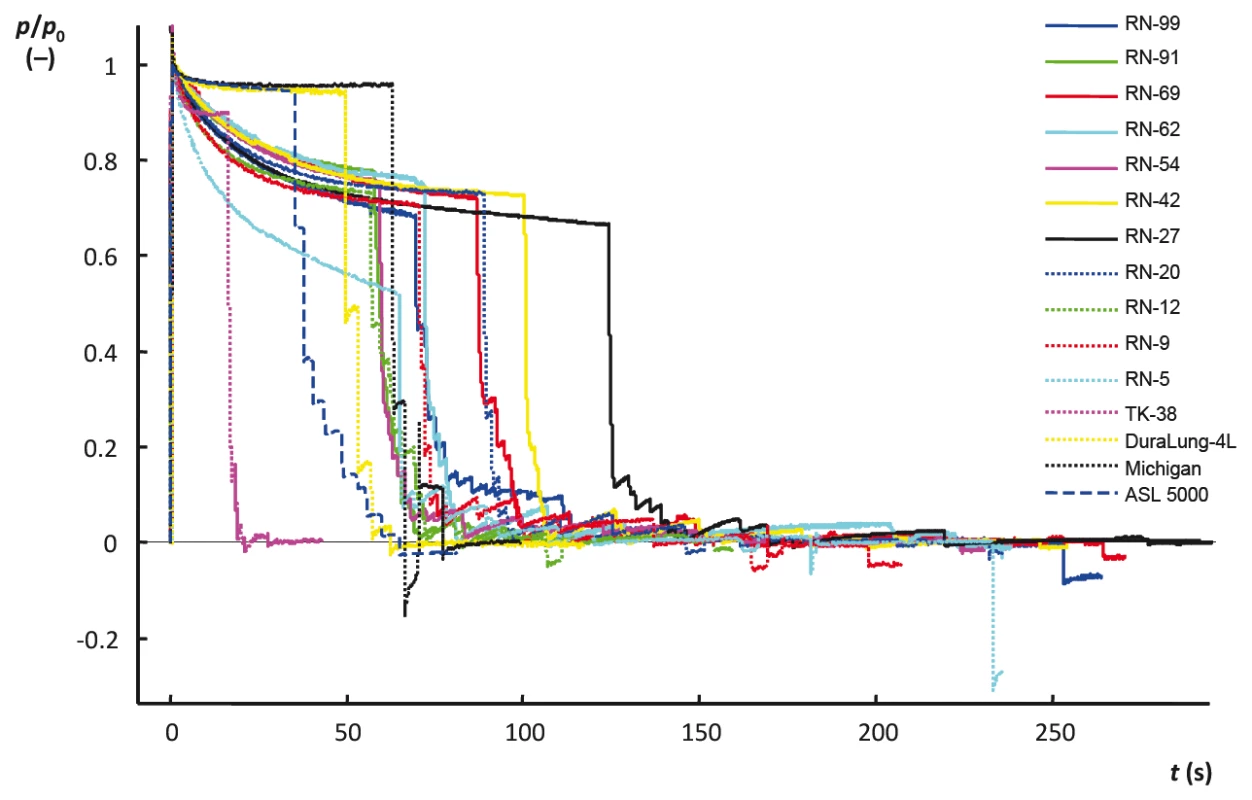
Na základě výsledků tohoto testu těsnosti byly provedeny úpravy modelů s cílem zjištěné netěsnosti odstranit. U většiny modelů se podařilo netěsnosti odstranit, jak je patrné z obrázků 5 a 6. Pokus o utěsnění byl však neúspěšný u čtyř modelů: RN-5, RN-9, RN-27 a RN-69.
5. Časový vývoj relativní hodnoty tlaku uvnitř modelů respirační soustavy po jejich rychlém naplnění vzduchem z kalibrační stříkačky. Hodnoty tlaku jsou pro jednotlivé modely respirační soustavy normalizo-vány vůči hodnotě tlaku <em>p</em><sub>0,3</sub>, která byla v příslušném modelu naměřena v čase 0,3 s od dokončení injekce vzduchu do modelu. Význam zkratek pro označení modelů respirační soustavy: DuraLung-4L – model DuraLung o objemu 4 L (South Pacific Biomedical, Temecula, CA, USA); Michigan-10 – model Dual Adult Test Lung 5600i (Michigan Instruments, Grand Rapids, MI, USA) s nastavenou poddajností 10 mL/cm H<sub>2</sub>O; TK-38 – termokompenzovaný model vyrobený na FBMI; RN-20, RN54 a RN-62 – nekompenzované modely vyrobené na FBMI z rigidních nádob. 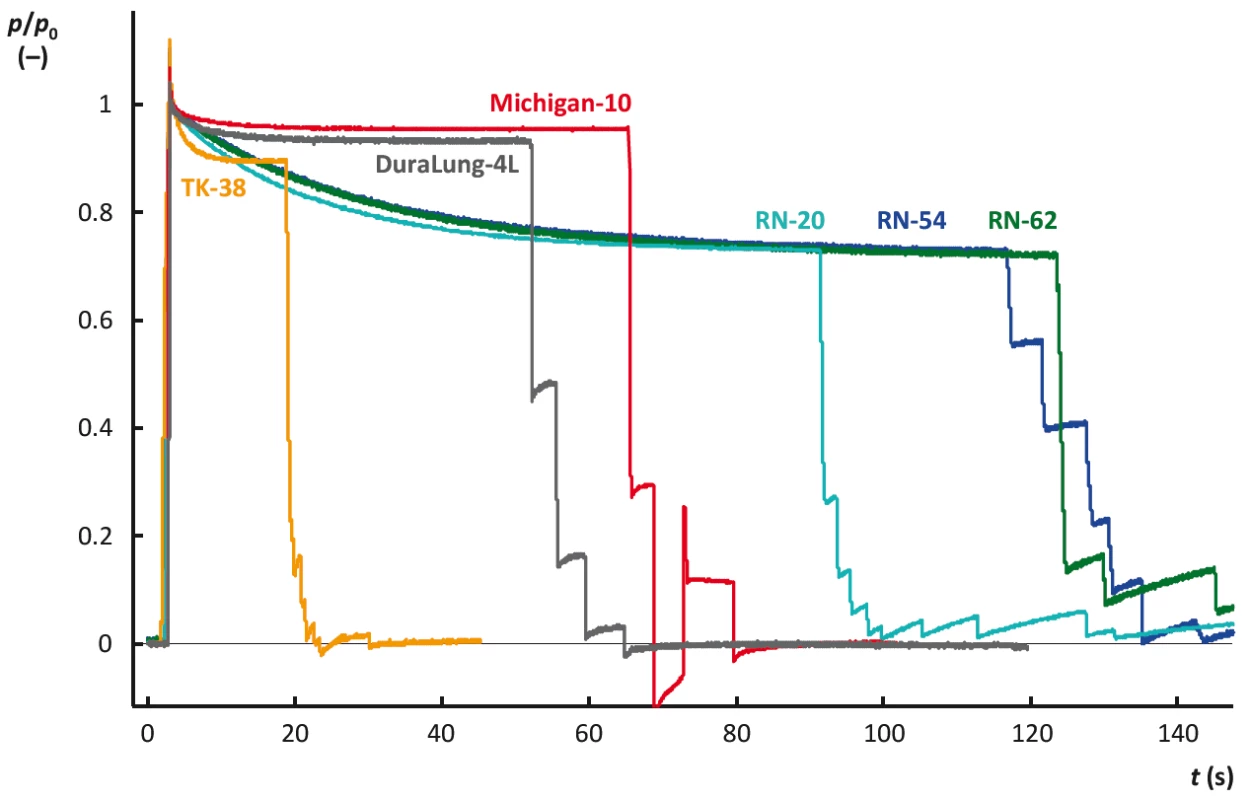
6. Porovnání tlakové odezvy modelu ASL 5000 s odezvami dalších modelů respirační soustavy. Hodnoty tlaku jsou pro jednotlivé modely respirační soustavy normalizovány vůči hodnotě tlaku <em>p</em><sub>0,3</sub>, která byla v příslušném modelu naměřena v čase 0,3 s od dokončení injekce vzduchu do modelu. Pro zpracování signálu z modelu ASL 5000 byly z původního signálu (světle modrá křivka) odstraněny oscilace (tmavě modrá křivka). Význam zkratek pro označení modelů respirační soustavy: DuraLung-4L – model DuraLung o objemu 4 L (South Pacific Biomedical, Temecula, CA, USA); Michigan-10 – model Dual Adult Test Lung 5600i (Michigan Instruments, Grand Rapids, MI, USA) s nastavenou poddajností 10 mL/cm H<sub>2</sub>O; RN-54 nekompenzovaný model vyrobený na FBMI z rigidní nádoby. 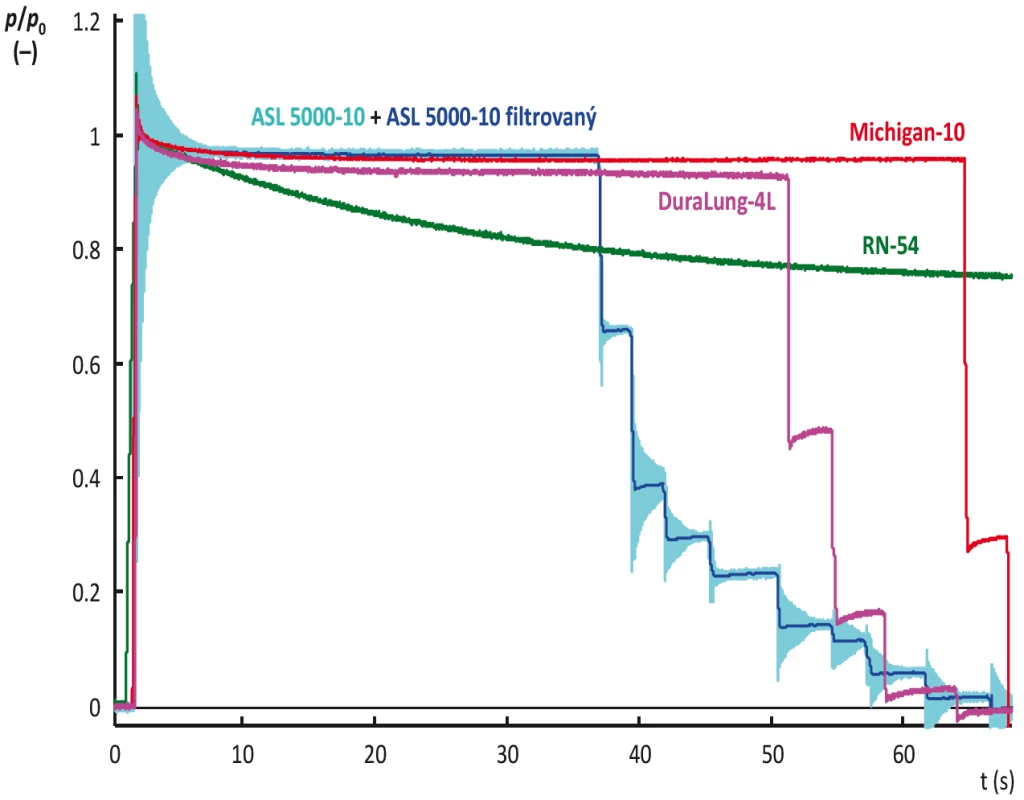
Následně byly změřeny poddajnosti, stanoven jejich charakter a zjišťovány netěsnosti jednotlivých modelů. Takto byly proměřeny všechny modely s neměnnou poddajností, tj. modely RN-5 až RN-99, model TK-38 a model DuraLung-4L. Zjištěné hodnoty adiabatických, efektivních a izotermických poddajností jsou uvedeny v Tabulce 1. Výsledky jsou vždy uvedeny jako průměrná hodnota z pěti měření opatřená směrodatnou odchylkou (μ ± s).
1. Hodnoty změřených poddajností studovaných modelů respirační soustavy, u nichž není poddajnost nastavitelná díky jejich konstrukci. 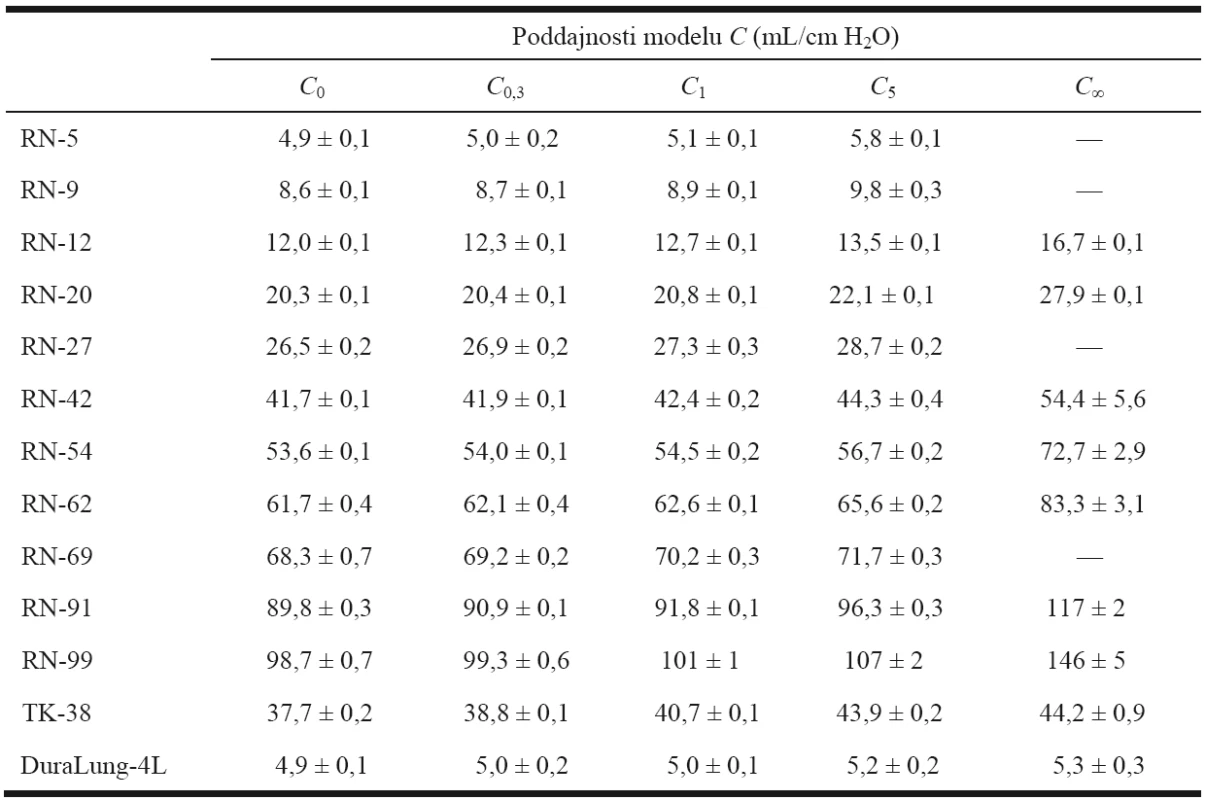
Vysvětlivky: C0 – adiabatická poddajnost; C0,3 – poddajnost změřená v čase 0,3 s od injekce vzduchu označovaná jako tzv. efektivní poddajnost; C1 a C5 – poddajnosti změřené v čase 1 s a 5 s od injekce vzduchu; C∞ – přibližná hodnota izotermické poddajnosti; tato hodnota není uvedena v případě, že při měření nedošlo k ustálení hodnoty tlaku v modelu v důsledku úniku vzduchu způsobeného neodstranitelnou netěsností modelu. Charakter chování jednotlivých modelů poddajností z hlediska rozdělení na izotermické a adiabatické modely je nejlépe patrný z Obrázků 5 a 6.
Na Obrázku 5 jsou zaznamenány časové průběhy tlaku po rychlé injekci vzduchu v modelech s pevnou poddajností hodnocených v Tabulce 1 a doplněné o křivku tlaku v modelu Michigan 5600i při zvolené poddajnosti 10 mL/cm H2O.
Normalizované křivky tlaku pro modely RN leží na sobě, proto jsou v grafu pro přehlednost uvedeny jen tři modely RN-20, RN-54 a RN-62. Odchylky křivek pro modely RN nejsou způsobeny jiným chováním modelu v závislosti na jeho objemu, ale odchylky křivek způsobuje i poměrně malá netěsnost.
Vlivem malé netěsnosti nejsou prakticky ovlivněny počáteční části křivek, ale únik plynu má za následek nemožnost ustálení hodnoty tlaku v modelu na konstantní hodnotě a tím i nemožnost určení izotermické poddajnosti C∞.
Na Obrázku 5 není pro přehlednost znázorněna tlaková křivka modelu ASL 5000. Odezva tohoto modelu na injekci plynu, a to jak rychlou, tak i pomalou, je periodická, jak ukazuje Obrázek 6. K ustálení hodnoty tlaku v tomto modelu, tj. k vymizení oscilací, prakticky nedochází. Z tohoto důvodu je obtížné i určit charakter chování modelu. Aby bylo možné charakter chování modelu ASL 5000 odhadnout, byly záznamy tlaku v modelu filtrovány a byly z nich odstraněny oscilace. Původní a filtrovaná hodnota tlaku v modelu ASL 5000 pro nastavenou poddajnost 10 mL/cm H2O je znázorněna taktéž na Obrázku 6 spolu s dalšími vybranými modely (DuraLung-4L, Michigan-10 a RN-54) pro možnost porovnání.
Pro hodnocení rozdílu chování modelu od čistě izotermického modelu a čistě adiabatického modelu jsou pro jednotlivé modely spočítány polytropické koeficienty, uvedené v Tabulce 2. Hodnoty polytropického koeficientu blízké číslu 1 svědčí o chování modelu blízkému ideálnímu izotermickému modelu a hodnoty blížící se adiabatické konstantě vzduchu κ = 1,4 naopak indikují podobnost s ideálním adiabatickým modelem.
2. Polytropické koeficienty (experimentálně zjištěné hodnoty) studovaných modelů respirační soustavy. 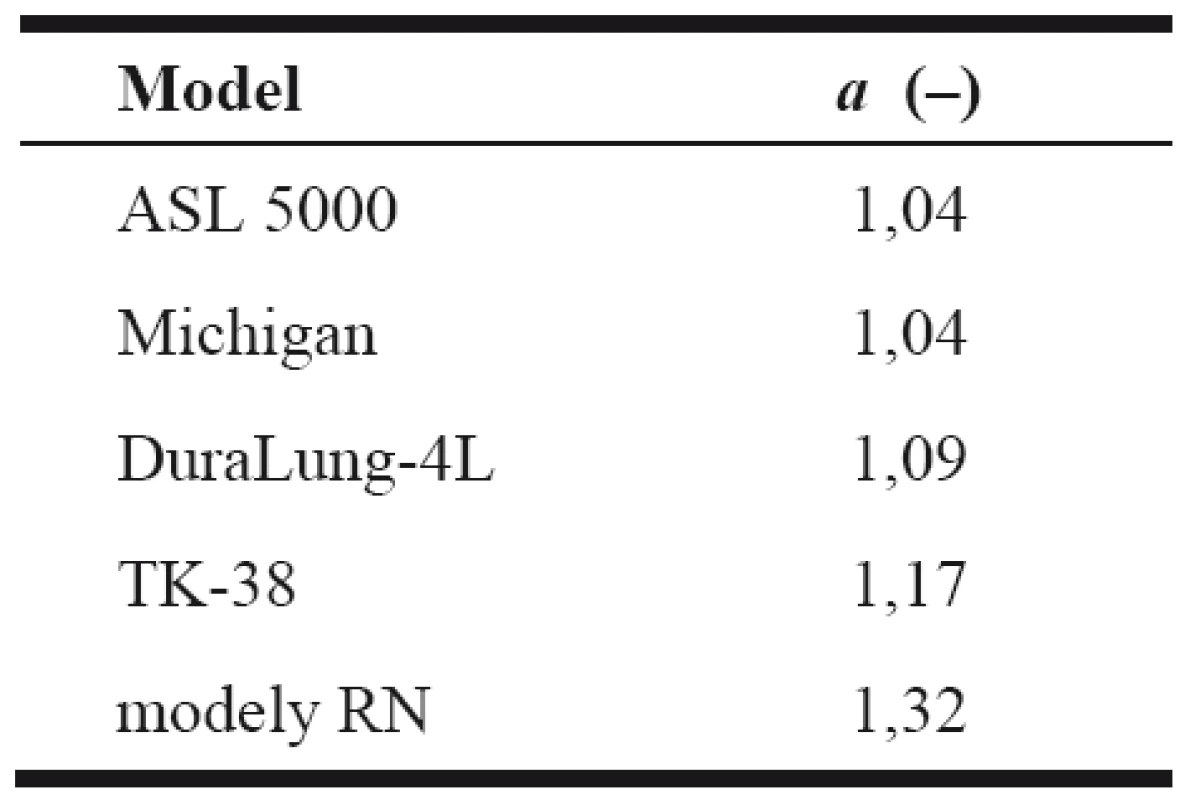
Z hodnocených modelů respirační soustavy mají charakteristiku blízkou ideálnímu izotermickému modelu pouze dva: ASL 5000 a Michigan 5600i. Jejich charakteristiky jsou dokonce lepší než charakteristiky obou testovaných termokompenzovaných modelů DuraLung-4L a TK-38. Chování modelů RN vytvořených z rigidních nádob se naopak přibližuje chování ideálního adiabatického modelu.
Diskuse
Primárním výsledkem této práce je jednoduše použitelná metoda určení poddajností fyzických modelů respirační soustavy a testování jejich těsnosti. Dále byl zaveden pojem tzv. efektivní poddajnosti, která nejlépe postihuje chování modelu při vlastním použití ve spojení s ventilátorem a konkrétním ventilačním režimem.
Společnou vlastností značné části analyzovaných modelů je jejich netěsnost, která způsobuje únik plynu z modelu při jejich použití. Dalším nepříjemným zjištěním je fakt, že model ASL 5000 vykazuje nestabilní odezvu na změnu objemu plynu v modelu,
která se projevuje vznikem velmi pozvolna tlumených oscilací tlaku uvnitř modelu.Jednotlivé modely byly charakterizovány hodnotami poddajnosti zjišťovanými v určitých časových okamžicích. Značná část modelů vykazuje únik plynu z důvodů netěsnosti. Ne vždy se však musí jednat o únik plynu pouze v modelu, přispívat k němu může i nedokonalá těsnost spojů jednotlivých částí aparatury, pístu kalibrační stříkačky a tlakoměru.
U značné části modelů je únik velmi malý. Díky tomu se neprojeví krátce po inflaci modelu a tím pádem neovlivní hodnotu adiabatické a efektivní poddajnosti. Dochází však ke stálému poklesu tlaku v modelu a nedojde k jeho ustálení, proto není možné zjistit poddajnost izotermickou. S ohledem na ventilační frekvence, které bývají používány v praxi, není nutné znát hodnotu izotermické poddajnosti modelu, protože parametry dechu spadají do časové oblasti, ve které se izotermická hodnota poddajnosti nemůže projevit. Tato disproporce mezi časovými charakteristikami dechu a dobou potřebnou k dosažení izotermické hodnoty poddajnosti platí i pro oba studované termokompenzované modely. Z uvedených vlastností je zřejmé, že pro praktické aplikace není podstatný rozdíl, zdali bude použit termokompenzovaný či nekompenzovaný model.
Překvapivým zjištěním je periodická odezva s poměrně vysokou frekvencí a pomalým tlumením u modelu ASL 5000 jako reakce na změnu objemu plynu v modelu. Model ASL 5000 je aktivní systém se zpětnovazebnou regulací a zjištěné oscilace jsou nejspíše touto regulací způsobeny. Tyto oscilace s velkou amplitudou a malým tlumením mohou při propojení modelu s ventilátorem způsobit neočekávané chování ventilátoru a mohou ovlivnit i hodnoty, které ventilátor měří a zobrazuje. Oscilace navíc znemožňují určení poddajnosti modelu z tlakové křivky, kdy není jasné, zda je nutné počítat s okamžitou hodnotou tlaku, nebo s hodnotou tlaku, kterou lze odečíst z křivky s již odfiltrovanými oscilacemi.
Z výsledků studia vlastností dostupných modelů respirační soustavy, zejména z křivek vývoje tlaku v modelech respirační soustavy po instilaci vzduchu, z vypočtených polytropických koeficientů (Tabulka 2) a následné diskuse lze učinit několik závěrů:
- Žádný z analyzovaných modelů, tj. ani termokompenzované modely, nemají chování odpovídající ideálnímu izotermickému modelu, tj. modelu plně tepelně kompenzovanému.
- Nejbližší chování podobné izotermickému modelu, tj. nejbližší chování skutečné respirační soustavě člověka, mají modely ASL 5000 a Michigan 5600i.
- Velmi podobné chování má též termokompenzovaný model DuraLung-4L.
- Termokompenzovaný model TK-38 má vlastnosti horší než výše hodnocené modely, nicméně vykazuje značnou redukci adiabatického chování.
- Modely z rigidních nádob RN mají všechny téměř stejné chování nezávislé na jejich objemu (tj. poddajnosti) a svým charakterem se blíží ideálnímu adiabatickému modelu.
- Pro praktické experimenty není rozhodující, zda má model spíše izotermické nebo adiabatické chování. V oblastech použitých ventilačních frekvencí (přesněji inspiračních a exspiračních časů) se všechny modely chovají obdobně a žádný z nich nevykazuje stabilní poddajnost v čase. Při ventilaci je s výhodou možné popsat všechny modely pomocí efektivní poddajnosti C0,3.
- Modely respirační soustavy zpravidla obsahují určitou netěsnost, a to i modely komerčně dostupné jako Michigan 5600i a ASL 5000. Většinou je však netěsnost malá a při běžných ventilačních frekvencích, a to včetně frekvencí při vysokofrekvenční ventilaci, se neprojeví, a proto neovlivňuje významně výsledky měření.
Závěr
Navržená metoda umožňuje snadné a opakovatelné měření poddajnosti a těsnosti modelů respirační soustavy. Se zavedením efektivní poddajnosti plic lze lépe popsat chování konkrétního modelu při konkrétním ventilačním režimu než při použití adiabatické či izotermické poddajnosti.
Poděkování
Tato práce byla podpořena z prostředků Ministerstva vnitra ČR projektem VG20102015062 Výzkumná podpora HZS ČR a dalších složek IZS ČR a z Operačního projektu Vzdělávání pro konkurenceschopnost (OPVK), projektu CZ.1.07/2.3.00/35.0021: Popularizace vědy a výzkumu ČVUT.
prof. Ing. Karel Roubík, Ph.D.
Katedra biomedicínské techniky
Fakulta biomedicínského inženýrství
České vysoké učení technické v Praze
nám. Sítná 3105, CZ-272 01 Kladno
E-mail: roubik@fbmi.cvut.cz
tel.: +420 603 479 901
Sources
[1] Roubík, K., Ráfl, J.: Poddajnost a resistance v rigidních modelech respirační soustavy. Lékař a technika, 2009, roč. 39, č. 1, s. 32–38. ISSN 0301-5491.
[2] Ráfl, J., Roubík, K.: Fyzické modely respirační soustavy a možnosti jejich využití. Lékař a technika, 2009, roč. 39, č. 1, s. 32–38. ISSN 0301-5491.
[3] IngMar Medical: ASL 5000TM Active Servo Lung, Breathing Simulator, User’s manual, Software 3.2. 2nd Revision, 2007.
[4] Vavřík D., Hájek M., Penhaker M.: Měření a vyhodnocení základních ventilačních režimů a poruch v simulačním ventilačním okruhu. (The measurement and evaluation of basic ventilation modes and failure simulations on ventilation circuit). Lékař a technika, 2008, roč. 38, č. 2, s. 191-194. ISSN 0301-5491.
[5] Penhaker, M., Vavrik, D: The measurement and failure simulations of basic ventilation modes. International Conference on Networking and Information Technology. 2010, Article number 5508451, pp. 554-556.
Labels
Biomedicine
Article was published inThe Clinician and Technology Journal

2014 Issue 1-
All articles in this issue
- Metallic nanoparticles affected by therapeutic ultrasound – The in vitro study of cell viability
- A method of compliance measurement and gastight testing in models of the respiratory system
- Rational operation of MRI equipment in university hospitals in the Czech Republic
- Individualization of head related transfer function
- Gene expression profiling after angiogenesis inhibitor treatment
- The effect of acetylsalicylic acid on angiogenesis in vitro
- The effect of docetaxel on molecular melting profile of DNA extracted from human breast adenocarcinoma MCF-7 cells
- The Clinician and Technology Journal
- Journal archive
- Current issue
- Online only
- About the journal
Most read in this issue- A method of compliance measurement and gastight testing in models of the respiratory system
- Rational operation of MRI equipment in university hospitals in the Czech Republic
- Metallic nanoparticles affected by therapeutic ultrasound – The in vitro study of cell viability
- Individualization of head related transfer function
Login#ADS_BOTTOM_SCRIPTS#Forgotten passwordEnter the email address that you registered with. We will send you instructions on how to set a new password.
- Career

