„Za hranice nejistoty“ – použití techniky one-way ANOVA současně pro odhad nejistoty měření a k verifikaci preciznosti měřicího postupu

Overview

Cíl:
předvést praktické použití softwarové techniky určené k analýze variance - one-way ANOVA - ke dvěma účelům verifikačního procesu: k odhadu nejistoty analytické metody dle dokumentu CLSI (Clinical and Laboratory Standards Institute) C51-A Vol. 32 No. 4 „Expression of Measurement Uncertainty in Laboratory Medicine, Approved Guideline“, 2012 [1] a současně ke zjednodušení postupu verifikace preciznosti měřicího postupu dle CLSI EP15-A2 Vol. 25 No.17 „User Verification of Performance for Precision and Trueness; Approved Guideline, Second Edition“ [2].

Výsledky:
aplikace obou normativních postupů je předvedena v praktickém příkladu odhadu nejistoty jedné koncentrační hladiny látkové koncentrace urey v lidském séru (měřená veličina) a současně ke zjednodušenému postupu verifikace preciznosti tohoto měřicího postupu. Verifikační experiment odpovídá dokumentu EP15-A2 a měření se prováděla na jedné koncentrační hladině měřené veličiny vždy ve třech opakováních v průběhu pěti dní.

Cíl - diskuse:
předvést možnost zjednodušení verifikačního postupu.

Závěr:
Pomocí techniky one-way ANOVA lze současně provést výpočet nejistoty měření i mezilehlé (celkové) preciznosti.

Klíčová slova:
CLSI C51-A [1], CLSI EP15-A2 [2], nejistota měření, preciznost, one-way ANOVA.

Úvod, vysvětlení pojmů

Prezentuji postup, jenž byl inspirován praktickým použitím dvou rozdílných dokumentů CLSI, a sice C51-A „Expression of Measurement Uncertainty in Laboratory Medicine, Approved Guideline“, dále jen C51-A, a dokumentem CLSI EP15-A2 „User Verification of Performance for Precission and Trueness; Approved Guideline-Second Edition“, dále jen EP15-A2. V tomto postupu se pomocí vhodné softwarové techniky současně plní dva rozdílné úkoly verifikačního postupu: výpočet resp. odhad nejistoty měření a verifikace preciznosti měřicího postupu.

Dokument CLSI C51-A je normativní návod určený pro odhad nejistoty měření v klinických laboratořích a jako takový předkládá více způsobů výpočtů odhadu nejistoty měření. Výpočet nejistoty měření je vždy odhadem infinitivním, tj. je vždy spojen s jistou mírou neurčitosti, jejíž velikost úzce souvisí s hodnotou měřené veličiny a matricí, v níž se stanovuje. Česká veřejnost již z mnoha předchozích velmi zasvěcených sdělení dobře zná termín „Top Down“ přístup. Ten představuje řešení problému, kterým se v i tomto sdělení rozumí zjednodušený odhad nejistoty měření a jehož cílem je z opakovaných měření vybraných vzorků zjistit celkovou rozšířenou kombinovanou standardní nejistotu měření použitelnou pro běžně měřené hladiny. Jedná se o postup zvláště vhodný pro uzavřené měřicí systémy, a proto se využívá především v rutinních zdravotnických laboratořích. Výhodou „Top Down“ přístupu pro jeho uživatele je jeho jednoduchost a s tím související menší finanční zátěž. Zjednodušený postup ale nemůže uživatele vést k lepšímu pochopení důležitých zdrojů nejistoty, k posouzení jejich skutečného příspěvku ke kombinované nejistotě, tím méně k rozkrytí možností jejich redukce či úplné eliminace. Odlišný, tzv. „Bottom-Up“ přístup si naopak klade za cíl předložit tzv. úplný nejistotní rozpočet, který právě výše uvedený zjednodušený „Top Down“ přístup neposkytuje.

Způsobům ověřování preciznosti měřicích postupů se rovněž věnuje obsáhlá literatura – viz odkazy. Čtenář v ní zjišťuje, že termín „preciznost“ je mírou pravého opaku, tj. nepreciznosti měření [3]. Bez ohledu na zbytečné spekulace, proč je nutno v odborné literatuře používat absurdní antonyma, faktem zůstává, že tato provozní charakteristika měřicího postupu nemá být například při verifikaci uživatelem IVD (in vitro diagnostických) systémů posuzována jen na základě pouhého testování opakovatelnosti měření (preciznosti v sérii), ale současně jako tzv. mezilehlá preciznost, kterou právě protokol EP15-A2 označuje jako preciznost celkovou resp. intra-laboratorní. Dvě zmíněné provozní charakteristiky metody, opakovatelnost a mezilehlou (celkovou) preciznost, již výrobci IVD uvádějí ve shodě s terminologií EP15-A2.

Dokument C51-A mj. popisuje, jak pro výpočet odhadu nejistoty měření použít analýzu variance jednoduchého třídění, techniku běžně v praxi známou jako one-way ANOVA, která se v českých překladech někdy označuje jako jednofaktorová resp. jednocestná ANOVA. Jedná se o základní softwarovou techniku analýzy rozptylu dat seskupených do sérií, provádí-li se opakovaná měření jedné a více hladin (hodnot) měřené veličiny ze stejného vzorku ve více sériích měření.

Dokument EP-15-A2 uvádí postupné kroky výpočtů určených k verifikaci různých provozních charakteristik metody a způsoby výpočtů lze s jistou nadsázkou označit za „manuální“. Jejich cílem je mj. odhad preciznosti měřicího postupu, tedy nejen opakovatelnosti (preciznosti v sériích), ale také preciznosti mezilehlé (celkové). Aplikaci techniky one-way ANOVA doporučenou v protokolu C51-A pro výpočet odhadu nejistoty měření lze současně použít i pro výpočet preciznosti měřicího postupu. Cílem tohoto sdělení je právě předvést, že základní postup uveřejněný v C51-A, byť tento slouží jinému cíli, lze aplikovat na účel, který obsáhle krokově řeší protokol EP15-A2. Níže je uveden příklad takového víceúčelového použití techniky one-way ANOVA, tedy nejen k odhadu nejistoty měření dle C51-A, ale primárně k odhadu preciznosti měřicího postupu, čímž je demonstrováno možné zjednodušení postupu prezentovaného v EP15-A2.

Postup

Budiž preciznost v rámci série měření (opakovatelnost) označena v souladu s EP15-A2 jako s_r a budiž dále preciznost mezi sériemi měření označeno jako s_b. Pak celková preciznost měření je označena jako s_i. Nechť dále u_c je kombinovaná standardní nejistota, která zahrnuje jak intra- tak inter- sériové složky nejistoty měření.

Výpočet preciznosti v sériích dle EP15-A2 se provádí dle rovnice:

(1)

kde:

D = celkový počet dní (5)

n = celkový počet opakování za den (3)

x_di = výsledek i-tého opakovaní dne d

x_d = průměr všech opakování/replikátů dne d

Výpočet preciznosti mezi sériemi dle EP15-A2 se provádí dle rovnice:

(2)

kde:

D = celkový počet dní

x_d = průměrná hodnota všech výsledků dne d

x = průměrná hodnota všech výsledků

Mezilehlá (celková) preciznost dle EP15-A2 se počítá dle rovnice:

(3)

kde n = počet měření v sérii.

Software one-way ANOVA označuje průměrný čtverec uvnitř sérií jako MS_wth a průměrný čtverec mezi sériemi MS_btw. Mezivýsledky představují jednak součet všech čtverců (SS) a počet stupňů volnosti (df) a hodnoty F a P poskytují měřítko významnosti rozdílů mezi sériemi měření.

Nechť SD (směrodatná odchylka) uvnitř série je v souladu s C51-A označena s_wth a v této podobě představuje míru nepreciznosti v sériích čili průměrnou preciznost v sériích a odpovídá tedy termínu opakovatelnosti měření, pak odhad opakovatelnosti se dle C51-A provádí přímo z hodnoty MS_wth následovně:

(1*)

V níže uvedeném příkladu bude dále dokázáno, že obě rovnice, (1) a (1*), poskytují stejný výsledek, tj. že: s_wth = s_r

Nechť SD mezi sériemi s_btw představuje míru nepreciznosti mezi sériemi čili průměrnou preciznost mezi sériemi, pak odhad preciznosti mezi sériemi s_btw se dle C51-A provádí z hodnot uváděných pod označením MS_btw, MS_wth a hodnoty n0 odpovídající počtu hodnot dostupných v každé sérii ze všech m zahrnutých sérií měření dle následujícího vztahu:

(2*)

kde MAX(a,b) je funkce „vyber maximální hodnotu z hodnot a a b“. Odtud, je-li MS_btw < MS_wth, pak s_btw = 0. V takových, byť zcela výjimečných případech se s_btw v souladu s EP15-A2 počítá následovně:

(2**)

Poznámka: tuto nepříjemnou, byť ověřitelně ojedinělou eventualitu resp. případ kdy MS_btw < MS_wth prakticky odstraňuje zvýšení počtu opakování měření ze tří na pět!

V příkladu níže bude dále dokázáno, že obě rovnice (2) a (2*) neposkytují stejný výsledek, tj. že:

Tedy že s_b dle EP15-A2 se od s_btw dle C51-A liší, a to tak, že výpočet s_b dle EP15-A2 poskytuje hodnotu vyšší nebo rovnou, neboť v hodnotě s_b je zahrnuta i s_r.

V C51-A není uveden adekvátní výpočet mezilehlé (celkové) preciznosti, označované v EP15-A2 jako s_i, ale v příkladu bude dokázáno, že tato odpovídá výpočtu dle rovnice (3*):

(3*)

Cílem příkladu je tedy poskytnut důkaz o tom, že výsledky obou výpočtů si (3) a (3*) jsou stejné!

Ve výjimečných případech, kdy hodnota MS_btw< MS_wth, se si v souladu s EP15-A2 počítá následovně:

(3**)

Pozn.: Mají-li všechny série stejný počet datových hodnot, pak datový soubor nazýváme vyvážený a n₀ je počet dat v každé takové sérii. Není-li tomu tak, pak se počet n₀ počítá následovně:

(4)

kde m = počet skupin, N =celkový počet pozorování, nj je počet dat v j-té skupině, nj je počet výsledků v j-té skupině, n je aritmetický průměr počtu výsledků v každé sérii, a s_n je SD n_j hodnot. Hodnota n₀ se musí pohybovat v rozmezí mezi nejmenší a největší hodnotou n_j. Je-li rozdíl mezi počty pozorování v každé skupině malý, představuje n obecně jejich adekvátní aproximaci.

Příklad aplikace techniky one-way ANOVA pro odhad preciznosti měřicího postupu a pro odhad nejistoty měření dle C51-A

Látková koncentrace urey v séru (S-Urea, mmol/l) byla měřena ve směsném lidském séru na přístroji Olympus AU 640, vždy ve třech opakovaných měřeních v každé sérii po dobu pěti dní (postup dle EP15-A2) (tabulka 1.). Získaný odhad celkové kombinované rozšířené nejistoty měření je vhodný pro následující jednotlivá měření stejné měřené veličiny ve stejném materiálu.

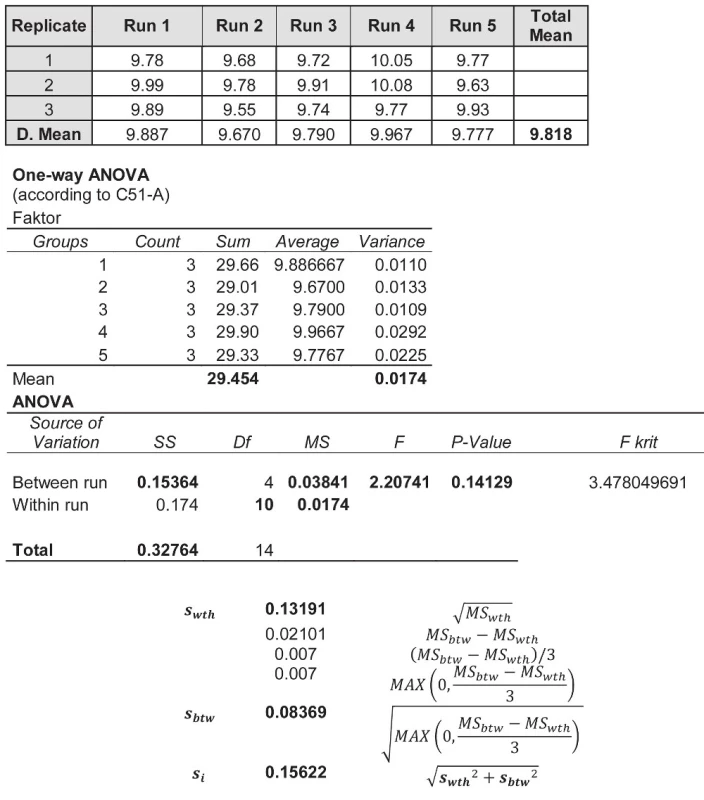
Komentář výpočtů

Průměrný čtverec mezi sériemi MS_btw = 0,03841 a průměrný čtverec uvnitř sérií MS_wth = 0,0174, kde n0 =3 je počet měření v sérii.

a) Odtud opakovatelnost s_wth dle C51-A počítaná podle rovnice (1*) činí:

a s_r dle EP15-A2 počítaná dle vztahu (1) a celý výpočet viz tabulka č. 2

Odtud vyplývá, že: s_wth = s_r

b) Preciznost mezi sériemi s_btw dle C51-A se počítá podle rovnice (2*)

Preciznost mezi sériemi s_b dle EP15-A2 počítaná podle rovnice (2) činí:

Odtud je zřejmé že s_b ≥ s_btw

c) Mezilehlá (celková) preciznost s_i se dle EP15-A2 počítá podle rovnice (3):

a s_i počítaná podle rovnice (3*):

Oba výpočty (3) a (3*) se liší, ale konečný výsledek s_i je stejný a postup ANOVA celý výpočet velmi zjednodušuje!

Nejistota měření

Dle nastavení experimentu platí, že s_wth a s_btw jsou vzájemně nezávislé proměnné. Pro kombinovanou nejistotu jednotlivého měření daného materiálu pak dle C51-A platí:

(5)

a pro celkovou rozšířenou kombinovanou nejistotu, kde k je koeficient rozšíření (k=2), platí:

(6)

Doplnění odhadu nejistoty měření o nejistotu plynoucí z korekce bias

Bias představuje numerické vyjádření pravdivosti stejně jako nepreciznost numerické vyjádření preciznosti. Každý odhad hodnoty bias je současně nevyhnutelně nejistý. Každá korekce měřené hodnoty o bias proto přispívá ke kombinované nejistotě. Korekce o známý bias tedy zlepší pravdivost vydaného výsledku, ale zvyšuje jeho nejistotu.

Z formálního úhlu pohledu platí, že přímou korekci potenciálního bias poskytuje při kalibraci použití komutabilního referenčního materiálu s udanou pravdivou hodnotou, uvedenou nejistotou a návazností. Přesto jsou výsledky měření v praxi ovlivňovány mnohými faktory, které sebelepší kalibrátory nemohou zcela vyřešit. Je proto nutno použít dodatečných způsobů odhadu bias, například vzájemné porovnávání výsledků vzorků pacientů stanovených buď různými metodami nebo přístroji či laboratořemi. Postupy odhadu bias jsou diskutovány v různých dalších dokumentech CLSI např., EP07 [3], EP09 [4] a EP15 [2]. Bias takto stanovený nemusí být sice shledán signifikantním, přesto nejistota plynoucí z jeho korekce, má být zahrnuta do kalkulace nejistoty výsledku. Na její odhad nejistoty typu A nebo B existují různé postupy, viz např. GUM [5]. Vztah, z něhož se vypočítává celková rozšířená kombinovaná nejistota včetně nejistoty zahrnující korekci bias je v tomto sdělení následující:

(7)

Bias (b_i) je odhadován jako rozdíl mezi výsledky měření stanovenými testovanou a referenční metodou, b_i = x_i - x_reference a je uváděn (stejně jako nejistota související s jeho korekcí) v jednotkách odpovídajících měření.

Odhad bias

(8)

Výpočet SD rozdílů

(9)

Výpočet SD odhadu nejistoty plynoucí z korekce bias jako střední chyby průměru (střední kvadratické chyby):

(10)

Pozn.: S pomocí techniky one-way ANOVA lze rovněž přímo provést odhad nejistoty průměrné hodnoty opakovaných měření například certifikovaného referenčního materiálu (CRM) x, která může posloužit jako adekvátní součást odhadu nejistoty měření odpovídající korekci bias. Platí, že je-li s_btw > 0, nejistota průměru měření u_c(x), činí:

(11)

kde n_total = celkový počet měření použitých v analýze. V případě, že s_btw= 0 nelze postup one-way ANOVA k výše uvedenému účelu použít. Pak postupujeme podle alternativního vztahu, který odpovídá vztahu (9):

(11*)

Odhad celkové kombinované nejistoty měření dle C51-A z výše uvedeného příkladu (S-Urea; látková koncentrace v mmol/l) se počítá podle rovnice (5):

⇒  a odtud odhad celkové rozšířené kombinované nejistoty měření podle rovnice (6):

Poznámka:

• u_c je odhadem nejistoty jednotlivého měření tohoto konkrétního materiálu za stejných podmínek
• u_t je odhad celkové rozšířené nejistoty bez nejistoty korigovaného bias, kde koeficient rozšíření = 2

Podle rovnice (7) lze provést odhad celkové kombinované nejistoty doplněný o nejistotu korigovaného bias výsledku testované metody, konkrétní příklad viz níže:

Předpokládejme, že počet měření cílených na pravdivost metody činil n = 4 a dále, že s(b) dle rovnice (9) je roven 1,24 mmol/l a odtud pak dle rovnice (10) s(b) = 1,24/ √ 4 = 0,62 mmol/l. Pak výpočet u_t resp. odhad nejistoty měření doplněný o nejistotu plynoucí z korekce bias dle rovnice (7) poskytne následující výsledek:

Nejistota měření, která nevyhovuje deklaraci výrobce IVD

Nesetká-li se odhad nejistoty měření konkrétního měřicího postupu získaný pomocí „Top-Down“ přístupu s očekávanými hodnotami předem pro daný postup specifikovanými výrobcem IVD nebo zjištěný odhad nejistoty měření nesplňuje zamýšlený účel výsledků [1], je nutné provést systematický přezkum zdrojů složek této nejistoty. V úvahu přichází způsob stanovení nejistoty měření označený jako „Bottom-Up“ přístup, který takové strukturované přezkoumání měřicího systému nabízí tím, že individuálně posuzuje jednotlivé komponenty přispívající k nejistotě měření. Pakliže však hodnota odhadu nejistoty měření vychází dle přístupu „Bottom-Up“ menší než dle přístupu „Top-Down“, měl by si uživatel provést řádnou revizi svého modelu vycházejícího z přístupu „Bottom-Up“ zacílenou dodatečně především na identifikaci možných, nezachycených či nedostatečně vyhodnocených složek nejistoty.

Závěr

Zabývám se problematikou odhadu nejistoty měření již řadu let a z ryze praktického hlediska si dovoluji tvrdit, že jedinou možností, jak mohou akreditované zdravotnické laboratoře zajistit svou povinnost zjišťovat a ověřovat nejistotu měření co nejjednodušším a postačujícím způsobem, je následovat výše uvedený postup dle „Top-Down“ přístupu. Pomocí analýzy variance (rozptylu) dat založené na technice one-way ANOVA lze provádět nejen výpočet odhadu nejistoty měření, ale i odhad preciznosti metody. Porovnáváním postupů dle dokumentů CLSI EP15-A2 a C51-A bylo shledáno, že „manuální“ postup výpočtu odhadu preciznosti dle EP15-A2 lze významně urychlit a zjednodušit použitím techniky one-way ANOVA, jehož aplikace je, byť pro jiný účel, uvedena v C51-A.

Závěrem děkuji RNDr. Zdeňku Kubíčkovi za velice podnětné odborné připomínky, které, jak doufám, zlepšily významně nejen jazykovou a stylistickou úroveň mého sdělení.

Do redakce došlo 17. 9. 2012

Adresa pro korespondenci:

MUDr. Jaroslava Ambrožová

Oddělení klinické biochemie a hematologie

Nemocnice Prachatice, a.s.

Nebahovská 1015

383 01 Prachatice

e-mail: ambrozova@nempt.cz